WYDZIAŁ MECHANICZNY	IMIĘ I NAZWISKO Wojciech Wszołek	ZESPÓŁ 6	OCENA OSTATECZNA
GRUPA 211c	TYTUŁ ĆWICZENIA Badanie pola magnetycznego za pomocą hallotronu	NUMER ĆWICZENIA 17	DATA WYKONANIA 14.11.2005

PRZYGOTOWANIE TEORETYCZNE

Zastosowany przez Halla układ doświadczalny przedstawiłem na poniższym rysunku.

W jednorodnym przewodniku, płynie prąd elektryczny w kierunku oznaczonym strzałką. Kiedy przewodnik ten umieścimy w polu magnetycznym prostopadłym do kierunku prądu między punktami

, leżącymi naprzeciwko siebie po obu stronach przewodnika, pojawia się napięcie elektryczne, które można wykryć woltomierzem. Znak tego napięcia zwanego napięciem Halla zmienia się, jeżeli zmieniamy kierunek prądu I albo kierunek pola magnetycznego B. Wartość napięcia Halla
okazuje się być proporcjonalna do wartości indukcji magnetycznej B i natężenia prądu I.

Siła Lorentza zaczyna działać na nośniki prądu po włączeniu pola magnetycznego. Jest skierowana prostopadle do
i do wektora indukcji B. Spowoduje ona zakrzywianie toru cząstek, więc na jednym z boków próbki wytworzy się nadmiar elektronów, będzie naładowany ujemnie przeciwny dodatnio. Wytworzy się pole elektryczne
prostopadłe do kierunku przepływu prądu, a zatem wytworzy się siła elektrostatyczna
i będzie rosnąć do czasu zrównania się z siłą Lorentza kierunek siły elektrostatycznej jest przeciwny do kierunku

siły Lorentza. Wpływ obu sił na ruch nośników kompensuje się.

Wyprowadzenie wzoru na napięcie Halla:

Z równowagi siły Lorentza z siłą elektrostatyczną wynika równanie:

stąd

ze związku pola elektrycznego z potencjałem Halla:

Z definicji natężenia prądu:

to

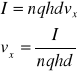
wstawiając dwa powyższe równania otrzymujemy:

skąd

n -koncentracja nośników prądu o ładunku q

h - grubość próbki

I - natężenie prądu przepływającego przez próbkę

B - wartość indukcji pola magnetycznego

- stała Halla.

Efekt Halla jest podstawą działania elementu elektronicznego zwanego hal­lotronem. Hallotrony wykorzystuje się przede wszystkim do wykrywania pola magnetycznego i pomiaru indukcji magnetycznej, zwłaszcza w maszynach elektrycznych.

Ponadto mogą być zastosowane m. in.

a)do pomiaru natężeń silnych prądów stałych,

b)mocy prądów stałych, zmiennych i szybkozmiennych,

c)jako elementy komputerów,

d)w urządzeniach przekształcających prąd stały na zmienny.

Aby uzyskać dużą wartość stałej y do wykonania hallotronów stosuje się najczęściej cienkie warstwy z półprzewodników typu n naparowane na cera­miczne podłoże. Wykorzystywane są następujące materiały: german, krzem. antymonek indu, arsenek indu, tellurek rtęci.

Wykonane z tego samego materiału hallotrony nie zawsze mają identyczne .rametry. Dlatego każdy hallotron posiada indywidualną charakterystykę.

Trudno jest praktycznie tak umieścić elektrody do pomiaru napięcia Halla, aby znajdowały się na jednej powierzchni ekwipotencjalnej. W związku z tym, na­wet w nieobecności pola magnetycznego, między tymi elektrodami istnieje zazwyczaj pewne napięcie
, zwane napięciem asymetrii, proporcjonalne do nat­ężenia prądu zasilającego hallotron. Mierzone napięcie wynosi zatem:

Wykonanie ćwiczenia

Zadanie1).Rysuję wykres zależności napięcia Halla od natężenia prądu zasilającego hallotron w stałym polu magnetycznym.

Lp.		UR[mV]	U[mV]	UH=U-UR[mV]
1	1	35	45	10
2	2	46	64	18
3	3	60	84	24
4	4	70	103	33
5	5	83	126	43
6	6	95	144	49
7	7	109	165	56
8	8	120	185	65
9	9	131	205	74
10	10	144	226	82

Zadanie 2).Dla każdej ustalonej wartości
wyliczam odpowiadającą jej indukcję pola magnetycznego w środku solenoidu ze wzoru :

Następnie rysuję wykres zależności
dla

Io=10mA			UR=145mV
Lp		U[mV]		UH=U-UR[mV]
1	600	180		35	828 10^-5
2	700	185		40	966 10^-5
3	800	190		45	1104 10^-5
4	900	195		50	1242 10^-5
5	1000	200		55	1380 10^-5
6	1100	205		60	1518 10^-5
7	1200	211		66	1656 10^-5
8	1300	216		71	1794 10^-5
9	1400	222		77	1932 10^-5
10	1500	227		82	2070 10^-5

Zadanie 3)

I0=10 mA UR0=146 mV Iso=1500mA
Lp.	z[cm]	U[mV]	UH=U-URO [mV]
1	-10	176	31
2	-9	184	38
3	-8	193	47
4	-7	201	55
5	-6	208	62
6	-5	214	68
7	-4	219	73
8	-3	223	77
9	-2	225	79
10	-1	227	81
11	0	229	83
12	1	229	83
13	2	229	83
14	3	229	83
15	4	227	81
16	5	225	79
17	6	222	76
18	7	218	72
19	8	214	68
20	9	207	61

Obliczam indukcje pola magnetycznego w środku solenoidu ze wzoru:

WNIOSKI

Badany hallotron jest elementem wrażliwym na zmiany położenia względem kierunku i zwrotu wektora indukcji magnetycznej. Ponieważ siła Lenza, mająca decydujące znaczenie w występowaniu zjawiska Halla zależy od sin kąta zawartego między kierunkami wektora prądu i wektora indukcji magnetycznej, więc zmiany tego kąta powodują zmiany napięcia Halla na wyjściu elementu.

4

---