3. Przestrzenie wektorowe

Przestrzeń liniowa V rozpięta nad ciałem liczbowym C jest to zbiór elementów, dla którego są spełnione podane dalej aksjomaty. Przestrzeń liniowa jest nazywana również przestrzenią wektorową, a jej elementy - wektorami. Elementy ciała C są skalarami.

Aksjomaty:

(1) zbiór V jest grupą abelową względem dodawania;

(2) dla dowolnego wektora v V i dowolnego skalara c C zachodzi

cv V; (5a)

(3) dla dowolnych wektorów v, u V i dowolnego skalara c C zachodzi

c(v + u) = cv + cu; (5b)

(4) dla dowolnego wektora v V i dowolnych skalarów c, d C zachodzi

(c + d)v = cv + dv; (5c)

(5) dla dowolnego wektora v V i dowolnych skalarów c, d C zachodzi

(cd)v = c(dv). (5d)

Jeżeli ciało C zawiera nieprzeliczalną liczbę elementów, to przestrzeń rozpięta nad tym ciałem nazywa się przestrzenią ciągłą. Jeżeli ciało C zawiera przeliczalną liczbę elementów, to przestrzeń jest nazywana przestrzenią dyskretną lub ziarnistą.

Przestrzeń Euklidesa jest przykładem przestrzeni ciągłej. Zbiór wszystkich możliwych n-pozycyjnych ciągów zero-jedynkowych stanowi przykład przestrzeni dyskretnej (binarnej).

Ciąg n-pozycyjny
którego elementy
są elementami ciała C, tworzy wektor v w przestrzeni liniowej V rozpiętej nad tym ciałem. Sumą dwóch wektorów
i
, u, v V, nazywamy wektor w, którego składowe są sumą składowych wektorów v i u

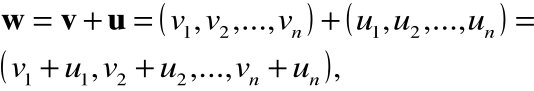
(6)

przy czym sumowanie
odbywa się ciele C i wynik sumowania jest elementem tego ciała.

Mnożenie wektora (ciągu) v przez skalar c będący elementem ciała C ma postać

(7)

przy czym każde mnożenie
odbywa się w ciele C.

Niech
będą wektorami w przestrzeni liniowej V rozpiętej nad ciałem liczbowym C. Dowolną sumę o postaci

, (8)

w której
są elementami ciała C, nazywamy liniową kombinacją wektorów
. O zbiorze k wektorów {
} mówimy, że jest liniowo niezależny jeśli dla dowolnie wybranego zbioru skalarów
zależność

(9)

zachodzi wtedy i tylko wtedy, gdy wszystkie
są równe zeru, tzn.

Jeżeli istnieje choć jeden zbiór
o elementach różnych od zera powodujący spełnienie równania (9), to zbiór wektorów {
} jest liniowo zależny. Na przykład wektory: (0,0,1), (0,1,0) i (1,0,0) są liniowo niezależne nad dowolnym ciałem, podczas gdy wektory: (1,1,1), (0,1,1) i (1,0,0) są liniowo zależne nad ciałem CG(2), ponieważ ich suma stanowi wektor zerowy.

Największa liczba liniowo niezależnych wektorów w przestrzeni stanowi wymiar przestrzeni. Wymiar przestrzeni jest nazywany również liczbą stopni swobody przestrzeni. Dowolny zbiór n liniowo niezależnych wektorów tworzy bazę przestrzeni
n- wymiarowej. Na przykład trzy wektory binarne (0,0,1), (0,1,0) i (1,0,0) są liniowo niezależne i tworzą bazę przestrzeni wektorowej V₃, zawierającej osiem wektorów binarnych: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1, 0, 0), (1, 0, 1), (1,1, 0), (1,1,1), będących kombinacjami liniowymi wektorów bazy nad ciałem CG(2).

Podzbiór P elementów przestrzeni liniowej V, który sam stanowi przestrzeń liniową, nazywamy podprzestrzenią liniową. Na przykład dwa wektory (0,0,1) i (0,1,0) tworzą nad ciałem CG(2) przestrzeń wektorową V₂, będącą podprzestrzenią przestrzeni V₃. Podprzestrzeń V₂ zawiera wektory: (0,0,0), (0,0,1), (0,1,0) i (0,1,1). Rozumując w podobny sposób, dochodzimy do wniosku, że wektor (1,1,1) jest bazą dla podprzestrzeni V₁, zawierającej tylko dwa wektory: (0,0,0) i (1,1,1).

4. Ciała rozszerzone

Opisane wcześniej operacje dodawania i mnożenia wektora przez skalar nie budzą wątpliwości. Operacje mnożenia i dzielenia wektorów nie są jednak równie oczywiste. Wprowadźmy przekształcenie

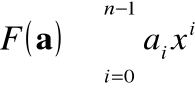
, (10)

które ciągowi
przyporządkowuje, w sposób wzajemnie jednoznaczny, wielomian

(11)

Na przykład dwupozycyjnym ciągom: (0,0), (0,1), (1,0), (1,1), stanowiącym wektory dwuwymiarowej przestrzeni rozpiętej nad ciałem CG(2), odpowiadają wielomiany pierwszego stopnia: 0, 1, x, x + 1. Dodawanie wielomianów sprowadza się do dodawania ich współczynników w odpowiednim ciele. W naszym przykładzie dodanie wielomianu
(0x + 1) do wielomianu (x + 0) daje w wyniku wielomian (x + 1), któremu odpowiada wektor (1,1) będący elementem rozpatrywanej przestrzeni. Spełniony jest więc aksjomat zamkniętości w odniesieniu do operacji dodawania. Aksjomat ten nie jest jednak bezpośrednio spełniony w odniesieniu do operacji mnożenia. Rzeczywiście, iloczyn wielomianów (x + 1) i (x + 0) daje w wyniku wielomian drugiego stopnia, który nie jest elementem zbioru wielomianów odpowiadającego rozpatrywanej przestrzeni. Przestrzeni n-wymiarowej odpowiada bowiem zbiór wielomianów stopnia nie większego niż (n - 1). Wyjściem z tej sytuacji jest zdefiniowanie wyniku mnożenia dwóch wielomianów jako reszty z podziału iloczynu przez pewien ustalony wielomian p(x) stopnia n. Dzięki tej definicji reszta z dzielenia jest zawsze wielomianem stopnia nie większego niż (n - 1). Wielomian p(x) musi być wielomianem pierwszym, tzn. wielomianem nie rozkładalnym w ciele CG(p). Formalnie wynik c(x) mnożenia wielomianów a(x) i b(x) zapisujemy w postaci

, (12)

przy jest resztą z podziału [] przez p(x).

Określimy teraz związek między wielomianami i ciałami. Zbiór wielomianów stopnia (m - 1) o współczynnikach będących elementami ciała CG(p) tworzy ciało CG(pm) z liczbą wielomianów równą pm. Na przykład Ciało CG(4) tworzy zbiór czterech wielomianów stopnia pierwszego o współczynnikach z ciała CG(2), to znaczy: {0, 1, x, x + 1}. Dodawanie wielomianów polega na dodawaniu ich współczynników w ciele CG(2). Wprowadzając wielomian pierwszy p(x) = x2 + x + 1, mnożenie wielomianów sprowadza się do określenia reszty z podziału ich iloczynu przez p(x). Tablice dodawania i mnożenia w ciele CG(4) mają postać:

+	0	1	x	x + 1				0	1	x	x + 1
0 1 x x + 1	0 1 x x + 1	1 0 x + 1 x	x x + 1 0 1	x + 1 x 1 0			0 1 x x + 1	0 0 0 0	0 1 x x + 1	0 x x + 1 1	0 x + 1 1 x

Ciało CG(4) składa się z czterech elementów, w tym element neutralny względem dodawania 0 i element neutralny względem mnożenia 1. Przyglądając się tablicy dodawania zauważamy, że każdy wielomian jest jednocześnie wielomianem odwrotnym ze względu na operację dodawania. Z tablicy mnożenia wynika, że każdy niezerowy wielomian ma również wielomian odwrotny: x jest wielomianem odwrotnym względem wielomianu x + 1 i wice versa, 1 jest - jak zawsze - również swoją odwrotnością. CG(4) jest więc rzeczywiście ciałem skończonym, będącym rozszerzeniem ciała prostego CG(2).

Ogólnie ciało skończone CG(pm) występuje dla dowolnej liczby pm, przy czym p jest liczbą pierwszą, a m - dodatnią liczbą całkowitą. Ciało CG(p) jest podciałem ciała CG(pm) w tym sensie, że elementy ciała CG(p) są podzbiorem elementów ciała CG(pm). Innymi słowy, ciało CG(pm) jest rozszerzeniem ciała CG(p). Na przykład ciało CG(2) jest podciałem ciała CG(4), takim że jego elementy {0,1} są podzbiorem elementów ciała CG(4): {0,1,x,x+1}. Ciało CG(4) jest jednocześnie rozszerzeniem ciała CG(2).

5. Wielomiany pierwotne

W każdym ciele Galoisa istnieje co najmniej jeden element pierwotny, oznaczany przez , charakteryzujący się tym, że jego potęgi reprezentują wszystkie elementy ciała z wyjątkiem zera. Na przykład w ciele CG(5) mamy 21 = 2, 22 = 4, 23 = 3 i 24 = 1, przy czym wartości 23 i 24 są obliczone modulo 5. Tak więc = 2 jest elementem pierwotnym ciała CG(5). Podobnie, = 3 jest także elementem pierwotnym ciała CG(5), ponieważ 31 = 3, 32 = 4, 33 = 2 i 34 =1. Weźmy pod uwagę teraz ciało CG(4) i spróbujmy sprawdzić czy = x jest elementem pierwotnym tego ciała. Obliczając kolejne potęgi , otrzymujemy: 1 = x, 2 = x +1 i 3 =0 = 1, przy czym wartości 2 i 3 są obliczone modulo p(x) = x2 + x + 1; = x jest więc elementem pierwotnym rozpatrywanego ciała. Łatwo sprawdzić, że kolejne potęgi = x +1 również generują wszystkie elementy ciała CG(4). W obu przykładach znaleźliśmy po dwa elementy pierwotne, z których każdy może być wykorzystany do wygenerowania wszystkich niezerowych elementów odpowiedniego ciała. Elementy każdego ciała skończonego możemy więc przedstawić na trzy różne sposoby: w postaci n-pozycyjnych ciągów binarnych, w postaci wielomianowej i w postaci potęg elementu pierwotnego, jak to przykładowo pokazano w tabeli 4 dla ciała CG(4). Zaletą reprezentacji potęgowej jest to, że mnożeniu dwóch elementów odpowiada sumowanie wykładników potęgowych. Na przykład przemnożenie x przez (x + 1) daje (x2 + x), a po obliczeniu reszty z dzielenia przez p(x) = x2 + x + 1 otrzymujemy 1. W postaci potęgowej ten sam rezultat uzyskujemy znacznie prościej:

Tablica 4

Elementy ciała CG(4)

Reprezentacjawielomianowa	Reprezentacja binarna	Reprezentacja potęgowa
0	00	Nie istnieje
1	01
x	10
x + 1	11

Wielomian p(x) stopnia m o współczynnikach z ciała podstawowego CG(p), którego pierwiastkiem jest element pierwotny nazywamy wielomianem pierwotnym. W tablicy D-6.5 pokazano wielomiany pierwotne stopnia od 2 do 25 o współczynnikach z ciała CG(2). Wielomiany te umożliwiają konstrukcję ciał rozszerzonych od CG(22) do CG(225).

Przedstawimy sposób tworzenia ciała rozszerzonego CG(pm), przy czym p jest liczbą pierwszą, a m - dodatnią liczbą całkowitą. Obliczamy najpierw wszystkie elementy ciała rozszerzonego, posługując się wielomianem pierwotnym p(x) stopnia m o współczynnikach z ciała podstawowego CG(p) i elementem pierwotnym = x , a następnie budujemy tablice dodawania i mnożenia. Ponieważ ciało CG(pm) jest rozszerzeniem ciała CG(p), to elementy ciała rozszerzonego są reprezentowane przez pm wielomianów stopnia (m - 1) lub mniejszego o współczynnikach z ciała podstawowego CG(p). Jeśli ciałem podstawowym jest CG(2), to współczynnikami wielomianów są 0 lub 1, a więc elementy ciała CG(2m) mogą być przedstawione za pomocą liczb binarnych.

Tablica 5

Wielomiany pierwotne o współczynnikach z ciała CG(2)

Stopień	Wielomian	Stopień	Wielomian
2		14
3		15
4		16
5		17
6		18
7		19
8		20
9		21
10		22
11		23
12		24
13		25

Pokażemy teraz przykładowo konstrukcję ciała CG(16) = CG(24), to znaczy p = 2 i m = 4. Z tablicy 5 odczytujemy wielomian pierwotny stopnia czwartego. Podnosimy kolejno do potęgi od zera do czternastej element pierwotny
, aby otrzymać zbiór wszystkich niezerowych elementów ciała CG(16): Wszystkie obliczenia wykonujemy oczywiście modulo p(x), na przykład

Zestawienie wszystkich elementów ciała CG(16) zawiera tablica 6.

Tablica 6

Elementy ciała CG(16) generowane przez wielomian

Reprezentacja potęgowa	Reprezentacja wielomianowa							Reprezentacja binarna	Reprezentacja heksadecymalna
Nie istnieje								0000	0
								0001	1
								0010	2
								0100	4
								1000	8
								0011	3
								0110	6
								1100	C
								1011	B
								0101	5
								1010	A
								0111	7
								1110	E
								1111	F
								1101	D
								1001	9

Dodanie dwóch elementów wymaga dodania w ciele CG(2) współczynników przy odpowiednich potęgach x, na przykład

Mnożenie dwóch elementów sprowadza się do sumowania (modulo 15) wykładników potęg elementu pierwotnego, na przykład

Pełne tablice dodawania i mnożenia w ciele CG(16) podano w tablicach 7 i 8.

Tablica 7

Tablica dodawania w ciele CG(16)

+	0	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
0	0	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
0	0	0	4	8	14	1	10	13	9	2	7	5	12	11	6	3
1	1	4	0	5	9	0	2	11	14	10	3	8	6	13	12	7
2	2	8	5	0	6	10	1	3	12	0	11	4	9	7	14	13
3	3	14	9	6	0	7	11	2	4	13	1	12	5	10	8	0
4	4	1	0	10	7	0	8	12	3	5	14	2	13	6	11	9
5	5	10	2	1	11	8	0	9	13	4	6	0	3	14	7	12
6	6	13	11	3	2	12	9	0	10	14	5	7	1	4	0	8
7	7	9	14	12	4	3	13	10	0	11	0	6	8	2	5	1
8	8	2	10	0	13	5	4	14	11	0	12	1	7	9	3	6
9	9	7	3	11	1	14	6	5	0	12	0	13	2	8	10	4
10	10	5	8	4	12	2	0	7	6	1	13	0	14	3	9	11
11	11	12	6	9	5	13	3	1	8	7	2	14	0	0	4	10
12	12	11	13	7	10	6	14	4	2	9	8	3	0	0	1	5
13	13	6	12	14	8	11	7	0	5	3	10	9	4	1	0	2
14	14	3	7	13	0	9	12	8	1	6	4	11	10	5	2	0

Tablica 8

Tablica mnożenia w ciele CG(16)

	0	^0	^1	2	3	4	5	6	7	8	9	^10	11	12	13	14
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
^0	0	^0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	0
2	0	2	3	4	5	6	7	8	9	10	11	12	13	14	0	1
3	0	3	4	5	6	7	8	9	10	11	12	13	14	0	1	2
4	0	4	5	6	7	8	9	10	11	12	13	14	0	1	2	3
5	0	5	6	7	8	9	10	11	12	13	14	0	1	2	3	4
6	0	6	7	8	9	10	11	12	13	14	0	1	2	3	4	5
7	0	7	8	9	10	11	12	13	14	0	1	2	3	4	5	6
8	0	8	9	10	11	12	13	14	0	1	2	3	4	5	6	7
9	0	9	10	11	12	13	14	0	1	2	3	4	5	6	7	8
10	0	10	11	12	13	14	0	1	2	3	4	5	6	7	8	9
11	0	11	12	13	14	0	1	2	3	4	5	6	7	8	9	10
12	0	12	13	14	0	1	2	3	4	5	6	7	8	9	10	11
13	0	13	14	0	1	2	3	4	5	6	7	8	9	10	11	12
14	0	14	0	1	2	3	4	5	6	7	8	9	10	11	12	13

6. Wielomiany minimalne

Każdy wielomian f(x) stopnia n ma n pierwiastków; jeśli wielomian f(x) jest wielomianem nierozkładalnym nad pewnym ciałem, to wszystkie jego pierwiastki są elementami ciała rozszerzonego. Na przykład wielomian jest wielomianem nierozkładalnym nad ciałem CG(2) i nie ma pierwiastków w tym ciele; ma natomiast cztery pierwiastki: 3, 6, 9, 12 z ciała rozszerzonego CG(16). Możemy to sprawdzić przez bezpośrednie podstawienie i skorzystanie z tablic dodawania i mnożenia (tab. 7 i tab. 8):

a więc
są rzeczywiście pierwiastkami wielomianu f(x). Możemy zatem przedstawić go w postaci co łatwo sprawdzić wykonując wskazane operacje:

Niech f(x) będzie wielomianem stopnia n o współczynnikach z ciała CG(2), nierozkładalnym w tym ciele. Niech będzie pierwiastkiem tego wielomianu, to znaczy f() = 0. Ponieważ f(x) jest wielomianem nierozkładalnym nad ciałem CG(2), to musi być elementem pewnego ciała rozszerzonego CG(2m). Przedstawimy teraz właściwości pierwiastka .

(1) Dla dowolnych
jest także pierwiastkiem f(x).

Innymi słowy,
są pierwiastkami f(x). Właściwość tę można wykazać następująco:

- rozważmy kwadrat wielomianu f(x)

Powtarzając tę procedurę, otrzymujemy

Wielomian f(x) jest określony nad ciałem CG(2), więc współczynniki fi mogą przyjmować wartość 0 lub 1; zatem
a więc

(13)

Z zależności (13) wynika, że dla dowolnego l 0

(14)

a dla x =

(15)

Z założenia jest pierwiastkiem wielomianu f(x), więc f() = 0, a zatem Dowiedliśmy więc, że jeśli element ciała CG(2m) jest pierwiastkiem wielomianu f(x) nad ciałem CG(2), to elementy
ciała CG(2m) dla wszystkich
są także pierwiastkami wielomianu f(x). Elementy
nazywamy elementami sprzężonymi z elementem . Na przykład wielomian jest wielomianem nierozkładalnym nad ciałem CG(2), ma natomiast cztery pierwiastki w ciele jednym z nich jest
, co łatwo sprawdzić przez podstawienie

Elementami sprzężonymi z
są:

Zauważmy, że dla l > (m - 1) = 3, elementy sprzężone powtarzają się, tak więc itd.

(2) Jeśli jest niezerowym elementem ciała CG(2m), to
jest zawsze równe jedności, można więc ułożyć równanie

(16)

z którego wynika, że jest pierwiastkiem wielomianu
nad ciałem CG(2). Jest to wielomian stopnia , ma więc pierwiastków będących niezerowymi elementami ciała CG(2m). Zerowy element tego ciała jest pierwiastkiem wielomianu (x). Elementy ciała CG(2m) tworzą więc wszystkie pierwiastki wielomianu

Wielomian najniższego stopnia o współczynnikach z ciała CG(2), którego pierwiastkiem jest element ciała CG(2m) nazywamy wielomianem minimalnym tego elementu.

Na przykład wielomian szesnastego stopnia , określony nad ciałem CG(2), ma szesnaście pierwiastków będących elementami ciała . Przedstawmy ten wielomian w postaci iloczynu wielomianów najniższych stopni

Każdy czynnik w tym rozwinięciu jest wielomianem minimalnym nad ciałem CG(2) pewnego elementu z ciała . I tak: wielomianem minimalnym elementu zerowego jest wielomian (x), wielomianem minimalnym elementu jednostkowego jest wielomian (x + 1); wielomianem minimalnym elementu
jest wielomian . Elementy
sprzężone z elementem
są także pierwiastkami wielomianu minimalnego . Elementy sprzężone mają więc taki sam wielomian minimalny. Wielomiany minimalne wszystkich elementów ciała zestawiono w tablicy 9.

Tablica 9

Wielomiany minimalne elementów ciała

Pierwiastki sprzężone	Wielomian minimalny
								+
						+		+
		+		+		+		+
						+		+
		+						+

Zauważmy, że każdemu elementowi odpowiada jeden i tylko jeden wielomian minimalny, różne elementy mogą jednak mieć ten sam wielomian minimalny; stopień wielomianu minimalnego nie jest większy niż m.

(3) Wielomian minimalny jest nierozkładalny w ciele CG(2). Element i elementy z nim sprzężone stanowią wszystkie pierwiastki wielomianu minimalnego, liczba pierwiastków określa stopień wielomianu. Niech e oznacza stopień wielomianu minimalnego; e jest najmniejszą liczbą całkowitą spełniającą równanie

(17)

Ponieważ element i elementy z nim sprzężone stanowią pełny zbiór pierwiastków wielomianu minimalnego, więc wielomian minimalny elementu można przedstawić w postaci

(18)

Na przykład elementami sprzężonymi z elementem
w ciele są:

Wielomian minimalny elementu
z ciała obliczony z wzoru (D6.18) ma więc postać

Jest to wynik zgodny z zawartością tablicy D-6.9.

(4) Wielomian minimalny elementu pierwotnego ciała ma stopień m i jest wielomianem pierwotnym. Ciało Galoisa tworzymy posługując się wielomianem pierwotnym p(x) stopnia m i elementem pierwotnym , będącym pierwiastkiem wielomianu p(x). Kolejne potęgi reprezentują wszystkie niezerowe elementy ciała . Tworzą one grupę multiplikatywną . W grupie obowiązuje aksjomat zamkniętości, ponieważ
To znaczy, to element ; a więc
jest elementem grupy .

6

---