1. Miary statystyczne /poziomu, zróżnicowania itd./ liczy się dla:
cech (zmiennych) zbiorowości
liczebności zbiorowości
2. Czy szereg statystyczny strukturalny można przekształcić w szereg strukturalny rzekomy i zatem obliczyć średnią harmoniczną:
tak
nie
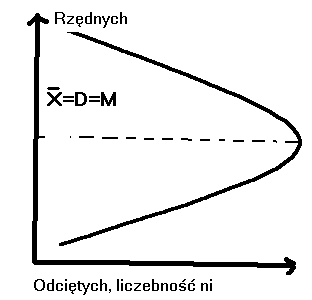
3. Odkładając na osi rzędnych odmiany
cechy, a na osi odciętych liczebności
zbiorowości wykazać graficznie, że
średnia arytmetyczna równa się medianie
i dominancie
/ ![]()
=M=D /
4. Moment centralny drugiego rzędu to:
jedna z właściwości średniej arytmetycznej
wariancja
5. Każdy związek korelacyjny jest zarazem stochastycznym.
Czy twierdzenie odwrotne jest słuszne?:
tak
nie
6. Gdy stosunek korelacji / exy / i współczynnik korelacji liniowej / rxy / to czy e²xy-r²xy jest:
miarą krzywoliniowości związku korelacyjnego
możliwością wykreślenia funkcji regresji
brakiem związku korelacynego
7. Przyjmując X-średnia arytmetyczna, D-dominanta, S /X/-odchylenie standardowe, napisać wzór współczynnika skośności:
![]()
8. Właściwą miarą dyspersji jest:
wariancja
odchylenie standardowe
9. Przyjmując X-średnia arytmetyczna, S /X/-odchylenie standardowe, napisać wzór współczynnika zmienności:
![]()
10. Przyjmując xi - dane empiryczne /rzeczywiste/, yi - dane teoretyczne /wyliczone /, oraz i =1,2,....n podać definicję metody najmniejszych kwadratów:
![]()
Suma kwadratów odchyleń danych rzeczywistych od danych teoretycznych ma być najmniejsza (minimalizowana)
11. Czy indeksy zespołowe mogą być uzyskane z indeksów indywidualnych ( prostych):
tak
nie
12. Przyjmując q- ilości, p- ceny, O- okres podstawowy, 1- okres badany napisać wzór na zespołowy indeks cen typu Paaschego:
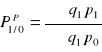
13. Równość Bortkiewicza określa:
relację indeksu Paaschego do indeksu Laspeyresa
możliwość spełnienia testu okrężnego
pozyskiwanie indeksów zespołowych z indeksów indywidualnych metodą średniej harmonicznej
14. Gdy dla dóbr A i B w okresie podstawowym /O/ i badanym /1 / mamy ilość /q/ i ceny/p/:
„O” „1”
q p q p
A 20 100 100 33
B 40 200 150 66
to indeksy zespołowe ilości /produkcji/ Laspeyresa i Paaschego:
są równe sobie
indeks Laspeyresa jest większy od indeksu Paaschego
indeks Paaschego jest większy od indeksu Laspeyresa
15. Współczynnik resztowy /K1/0/ dla indeksu Fishera równa się:
0
-2
1
16. Indeksy produkcji /ilości/ o stałej strukturze wag. to indeksy:
jednopodstawowe typu Laspeyresa
jednopodstawowe typu Paaschego
łańcuchowe typu Laspeyresa
łańcuchowe typu Paaschego
17. Przyjmując q -ilości, p -ceny, t -nakład pracy, O -okres podstawowy, 1-okres badany;
napisać wzór na ilościowy indeks wydajności pracy typ Paaschgo:
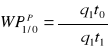
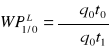
Wyszukiwarka
Podobne podstrony:
Test statystyka, Statystyka
test statystyka, Statystyka Opisowa
test 3 statystyka, Statystyka testy
Rachunek prawdopodobieństwa i statystyka, Rachunek prawdopodobieństwa i statystyka/Test 2: Statystyk
test- 3-statystyka, Statystyka testy
statystyka test I, Statystyka
test statystyka
test, Statystyka
Statystyka TEST, Zarządzanie i inżyniernia produkcji, Statystyka
Test t dla danych skorelowanych wzór tabel, statystyka, statystyka
Statystyka Test T Kuszewski
statyst wyprac, test t, test t-Studenta pozwala porównywać średnie w grupach niezależnych
Test ze statystyki z zima 2007 grupa A[1], 1)
Test ze statystyki 2007 (z wykładu), 1)
statystyka test 3
statystyka test 2
Test ze statystyki biały sugerowane rozwiązanie
więcej podobnych podstron