Analiza szeregów czasowych

Szeregiem czasowym nazywamy ciąg wartości zmiennej uporządkowanej zgodnie z następstwem momentu lub wartości czasu , których tego dotyczą.

Jest to zbiór obserwacji statystycznych charakteryzujących zmiany poziomu zjawiska w czasie. Poszczególne obserwacje nazywamy wyrazami tego szeregu.

Szereg czasowy zapisujemy za pomocą symbolu
lub
gdzie t reprezentuje kolejne momenty lub okresy czasu.

Momenty lub okresy są oznaczone kolejnymi liczbami całkowitymi np. 1992, 1993, 1994 itd.

• w ogólności mogą to być dowolne liczby n, których każda następna jest większa

od poprzedniej. Zmienna czasowa jako wielkość niezależna jest zmienną ciągłą.

Zapis szeregu czasowego
lub
pokazuje, że należy traktować ten szereg jako funkcję czasu. Wyróżnia się dwa rodzaje szeregu czasowego.

1. szeregi czasowe momentów - ich wyrazy odpowiadają jednakowo odległym momentom czasu. Szeregi momentów podają stan liczbowy zbiorowości w ściśle określonych momentach lub sumę wartości pewnej zmiennej posiadanej przez jednostki populacji.

( np. liczba ludności Polski w dniu 31.12. kolejnego roku .Liczba statków polskiej floty handlowej - stan liczebny cechy tworzącej zbiorowość, pojemność statków - suma wartości cechy tworzącej zbiorowość )

Dodawanie wyrazów szeregu czasowego momentów jest pozbawione sensu.

2. szeregi czasowe okresów - ich wartości odpowiadają okresom czasu o jednakowej

długości. Wyrażają one poziom zjawiska lub liczbę faktów, które zaszły w kolejnych

okresach. ( np. produkcja telewizorów w Polsce, eksport owoców i warzyw. Liczba

faktów może być przedmiotem szeregu , liczba zgonów, liczba zawartych małżeństw,

liczba wypadków ).

Dodawanie wyrazów szeregu czasowego okresów jest zasadne.

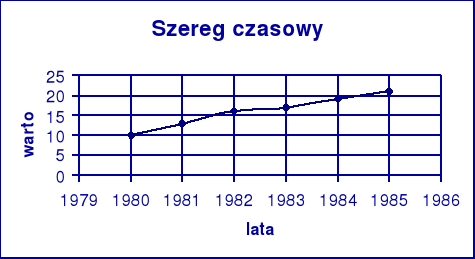
Szeregi czasowe ilustrujemy za pomocą wykresów sporządzanych w układach współrzędnych ograniczonych do I - szej ćwiartki dodatnich wartości. Na osi odciętych - okresy, na osi rzędnych - wielkość zjawiska. Wykres jest liniowy.

Zagadnienia ogólne dotyczące szeregu czasowego.

Wyrazy szeregu czasowego powinny być wielkościami jednolitymi w czasie tzn. jednorodnymi i porównywalnymi. Należy to rozumieć w ten sposób, że w całym analizowanym okresie szereg powinien dotyczyć jednego i tego samego zjawiska lub zbiorowości, definiowanego i mierzonego w ten sam sposób.

Zmiany granic obszarów organizacyjnych jest powodem zerwania jednolitości w czasie.

Badanie dynamiki zjawisk w czasie.

Istnieje parę sposobów badania dynamiki zjawiska. Zadaniem tego badania jest określenie zmian zachodzących w poziomie danego zjawiska oraz kierunku , tempa i intensywności. Jednym z narzędzi badania dynamiki są wskaźniki dynamiki. Jeżeli zjawisko jest jednorodne lub właściwie zagregowane to obliczenie współczynników sprowadza się do dzielenia lub odejmowania dwóch wyrazów szeregu czasowego. Wskaźniki dynamiki mogą być wyznaczane dla dwóch wybranych okresów lub momentów lub dla całej ich sekwencji.

Jeżeli wielkość zjawiska w kolejno po sobie następujących momentach lub okresach odnosimy stale do pierwszego wybranego wyrazu szeregu to wskaźniki nazywamy jednopodstawowymi.

Jeżeli natomiast wielkość zjawiska w kolejno po sobie następujących okresach lub momentach odnosimy do wielkości zjawiska lub momentu poprzedzającego to wskaźniki nazywamy łańcuchowymi ( sekwencja zjawisk ). Jeżeli chodzi o konstrukcję wskaźników to wyróżniamy następujące:

1. Przyrosty absolutne
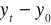
   - przyrost jednopodstawowy

- przyrost łańcuchowy

Przyrosty absolutne informują o ile jednostek zmieniło się ( wzrosło lub zmalało ) zjawisko w okresie lub momencie badanym względem okresu lub momentu poprzedniego lub podstawowego. Jeżeli wielkości wyrażamy w jednostkach to różnice też wyrażamy w tych samych jednostkach. Przyrosty absolutne są liczbami mianowanymi.

2. Przyrosty względne -
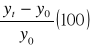
   - przyrost jednopodstawowy

-
- przyrost łańcuchowy

Uzyskujemy je przez dzielenie przyrostów absolutnych przez wielkość zjawiska w okresie lub momencie odniesienia.

Przyrosty względne informują o ile w wyrażeniu względnym (%) zmieniło się ( wzrosło lub zmalało ) zjawisko w drugim okresie lub momencie w stosunku do okresu lub momentu podstawowego lub poprzedniego. Jeżeli zjawisko wzrosło to przyrost wyraża się liczbą dodatnią, jeżeli zmalało to przyrost wyraża się liczbą ujemną.

Przykład:

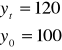
jednostek

Wzrost o 20 jednostek co stanowi 20% podstawy.

Indeksy dynamiki

Indeksy dynamiki uzyskujemy dzieląc wielkość zjawiska w danym okresie lub momencie przez wielkość zjawiska w okresie lub momencie podstawowym lub poprzednim.

- indeks jednopodstawowy

- indeks łańcuchowy.

Indeks dynamiki informuje ile razy w ujęciu względnym zjawisko w danym okresie lub momencie jest większe lub mniejsze w stosunku do okresu lub momentu podstawowego lub poprzedniego.

Przykład:

- stanowi 120 % zjawiska z poziomu 0.

Odjęcie od indeksu dynamiki liczby 1 lub 100% da odpowiedni przyrost względny.

Jeżeli zjawisko wzrasta to indeks dynamiki jest >1.

Jeżeli zjawisko spada to indeks dynamiki jest < 1.

Najczęściej stosowanymi indeksami dynamiki są indeksy dynamiki ujęte w procentach.

W Roczniku Statystycznym indeksy są uzupełniane indeksami dynamiki.

Indeks jednostkowy - 1995 = 100%

Indeks łańcuchowy - rok poprzedni = 100%

Indeksy agregatowe.

Agregatowe indeksy dynamiki

1. 
   
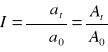
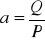
   (ilość / cena)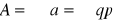

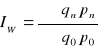
2. 
   
   (późniejszy okres / wcześniejsze odniesienie)

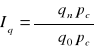
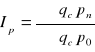
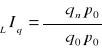
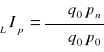
L - indeks Laspeyersa 0

P - indeks Paascha n

Tablica większa niż 2x2 nazywana jest tablicą kontyngencyjną

Jeżeli cech A i B są niezależne to zachodzi :

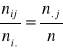
- liczebność teoretyczna

- cechy są niezależne

- czym większe różnice tym większa zależność

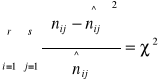
- kontyngencyjność kwadratowa

- cechy są zależne
- cechy są niezależne

( cechy są niezależne)

( cechy są zależne )

stopnie swobody

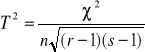
- współczynnik zbieżności (korelacji) Czupurowa

rxr - tablica kwadratowa

rxs - tablice niekwadratowe

Zadanie:

Pewien produkt można wytwarzać trzema metodami produkcyjnymi. Wysunięto hipotezę, że wadliwość produktów nie zależy od metody produkcji. Wylosowano niezależną próbę 276 sztuk wyrobu i otrzymano następujące wyniki badania jakości dla poszczególnych metod. Dla istotności
zweryfikować hipotezę o niezależności jakości od metody produkcji i policzyć współczynnik Czupurowa.

Jakość	Metoda produkcji I			Metoda produkcji II			Metoda produkcji III			Razem
Dobra	1,333		44,4	1,905		177,8	0,833		44,4
			40			80			60		180
		33,3		6,7	93,3		-13,3	53,3		6,7
	Zła	2,667		44,4	3,81		177,8	1,667		44,7
			10			60			20		90
		16,7		-6,7	46,7		13,3	26,6		6,7
	Razem
			50			140			80		270

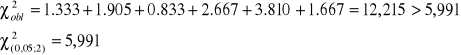
5,991

- należy do zbioru krytycznego
.

Wniosek: jakość zależy od metody produkcji. Hipotezę
odrzucamy.

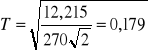
Zależność nie jest wysoka.

Analiza dynamiki (analiza szeregów czasowych)

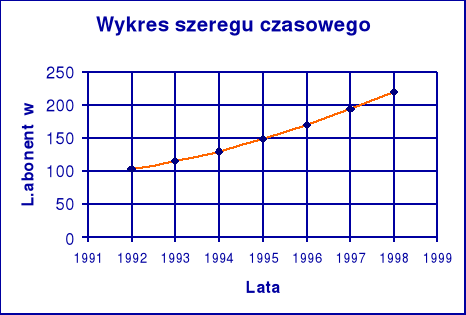
Liczba abonentów telefonii cyfrowej na tysiąc ludności kształtowała się następująco:

Lata	Liczba abonentów
1992	102,5	0	0	1
1993	114,7	12,2	1,119024	1,119024
1994	129,8	15,1	1,131648	1,266341
1995	148,4	18,6	1,143297	1,447805
1996	169,1	20,7	1,139488	1,649756
1997	193,1	24	1,141928	1,883902
1998	219,4	26,3	1,136199	2,140488
Suma	X	116,9	X	X

1. Jaki jest szereg czasowy (momentów) określa stan liczebny zbiorowości ( przeliczony na 1000 mieszkańców )

2. 
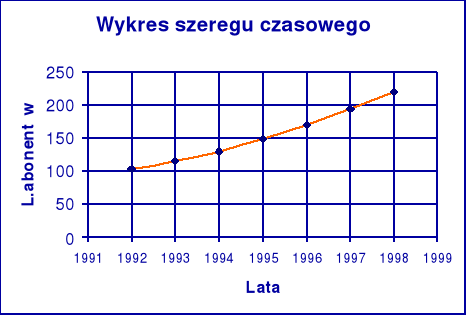
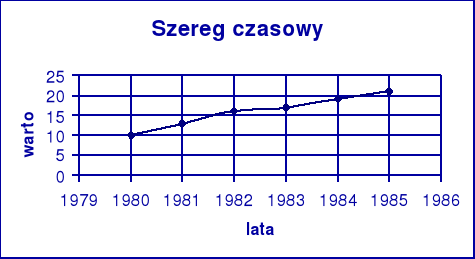
   Wykres szeregu czasowego.

3. Scharakteryzować dynamikę zjawiska za pomocą wskaźników indywidualnych

1. Przyrost absolutny łańcuchowy
   

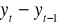
2. Indeksy łańcuchowe
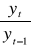
   (100)

3. Indeksy jednopodstawowe
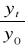
   (100)

Musimy zastosować średnią geometryczną

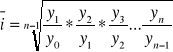
- średni indeks zmian

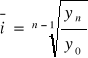
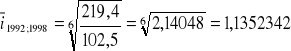
wzrost abonentów

Zadanie:

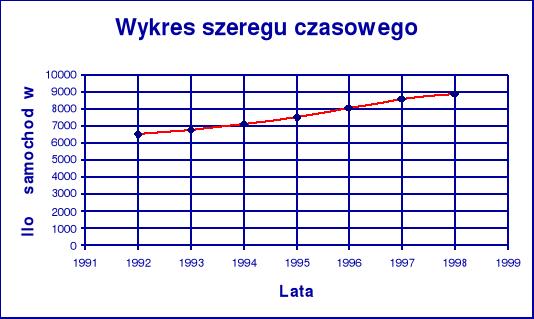
W latach 1992 - 1998 liczba samochodów zarejestrowanych w tysiącach sztuk była następująca:

Lata	Liczba samochodów w tys. szt.
1992	6505	0	0	1
1993	6771	266	1,040892	1,040892
1994	7153	382	1,056417	1,099616
1995	7517	364	1,050888	1,155573
1996	8054	537	1,071438	1,238125
1997	8533	479	1,059474	1,31176
1998	8891	358	1,041955	1,366795
Razem		2386	X	X

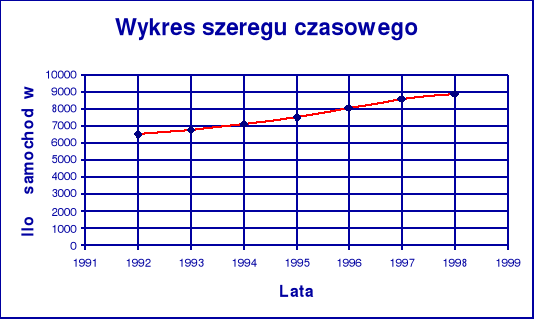
wzrost ilości zarejestrowanych samochodów

---