MODELE ZACHOWANIA SIĘ FIRMY NA RYNKU KONkUrenCYJNYM
Z teorii wyboru konsumenta wiemy, że kieruje się on kryterium maksymalizacji użyteczności przy swoich ograniczeniach budżetowych Zasadniczym motywem działania firmy jest maksymalizacja zysku bądź też minimalizacja kosztów. Zajmiemy się firmą, która działa w warunkach konkurencji doskonałej (czystej) tzn. spełniony jest układ następujących założeń:
na rynku jest dostateczna ilość firm, które wytwarzają ten sam produkt,
firma nie ma wpływu na ceny (jest cenobiorcą),
rynek jest chłonny tzn. firma nie ma problemu ze zbytem własnych produktów i z nabyciem potrzebnych czynników produkcji,
nie ma żadnych barier wejścia na rynek i wyjścia z rynku,
otoczenie rynkowe jednakowo oddziałuje na wszystkie firmy (przepisy prawne, dostęp do informacji itd.).
Pierwsze zadanie producenta (maksymalizacja zysku)
Dla prostoty rozważań zakładać będziemy, że analizowana przez nas firma wytwarza tylko jeden produkt, do którego produkcji zużywa n czynników produkcji. Proces produkcji tej firmy opisuje skalarna funkcja produkcji f, o której zakładamy, że spełnia wcześniejsze założenia (1-4). Celem działalności firmy jest maksymalizacja jej zysku.
Rozważać będziemy strategię przedsiębiorstwa, w której nie ma ograniczeń na czynniki produkcji. Matematycznie zadanie to możemy sformułować w postaci:
wyznaczyć maksymalny zysk przedsiębiorstwa
![]()
przy ograniczeniu ![]()
, gdzie p- to cena wytwarzanego przez firmę produktu, ![]()
jest wektorem cen czynników produkcji, ![]()
jest wektorem czynników produkcji, ![]()
jest przychodem firmy a ![]()
to koszty firmy.
Twierdzenie
Jeżeli są spełnione wcześniej uczynione założenia oraz warunek:
![]()
lub w postaci skalarnej
![]()
dla i=1,…,n
wówczas zadanie maksymalizacji zysku producenta ma dokładnie jedno dodatnie rozwiązanie ![]()
, które wyraża się przez rozwiązanie układu równań:
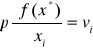
dla ![]()
Ilustracja jednowymiarowa.
Z uczynionych założeń wnosimy, że warunek konieczny istnienia maksimum jest tutaj również warunkiem dostatecznym istnienia rozwiązania optymalnego.
![]()
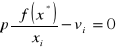
dla i=1,…,n
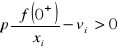
![]()
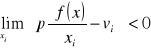
![]()
A to oznacza, że rozwiązanie optymalne ![]()
i jest jedyne.
Uwaga
Wyrażenie ![]()
nazywamy krańcową produkcyjnością i-tego czynnika produkcji w sensie wartościowym.
Z powyższego twierdzenia wynosimy, że krańcowa produkcyjność i-tego czynnika w sensie wartościowym jest równa cenie tego czynnika ![]()
dla produkcji optymalnej.
Def. (funkcja popytu na czynniki produkcji)
Niech dane będzie przedsiębiorstwo, które realizuje zadanie maksymalizacji swojego zysku przy danej cenie własnego produktu ![]()
i przy danym wektorze ![]()
środków produkcji.
Funkcję ![]()
taką, że ![]()
gdzie ![]()
jest optymalną wielkością czynników produkcji w zadaniu maksymalizacji zysku, nazywamy funkcją popytu na czynniki produkcji (tej firmy).
Uwaga
Funkcja popytu na czynniki produkcji opisuje zmiany wielkości czynników optymalnej produkcji firmy w zależności od ceny produktu i ceny czynników produkcji (analogiczna rola do funkcji popytu Marshalla w teorii konsumenta).
Twierdzenie
Jeśli są spełnione uczynione założenia to funkcja popytu na czynniki produkcji jest dodatnio jednorodna stopnia zero.
Def. (funkcja podaży)
Przy poprzednich założeniach funkcja ![]()
gdzie ![]()
nazywamy funkcją podaży firmy.
Uwaga
a) Funkcja podaży produktu opisuje jak zmienia się optymalna wielkość produkcji firmy w zależności od zmiany ceny produktu i zmiany cen czynników produkcji. Ma ona analogiczne własności jak funkcja popytu na czynniki produkcji.
b) Dodatnia jednorodność stopnia zero zarówno funkcji popytu na czynniki produkcji jak i funkcja podaży informuje nas, że wielkości te nie zależą od poziomu cen a tylko od ich struktury.
Def ( funkcja optymalnego zysku)
Przy poprzednich założeniach funkcję:
![]()
nazywamy funkcją optymalnego zysku zależną od cen produktu i środków produkcji.
Twierdzenie (własności funkcji optymalnego zysku)
Funkcja optymalnego zysku ma następujące własności:
jest rosnąca względem ceny produktu,
jest malejąca wzglądem cen czynników produkcji,
jest dodatnio jednorodna stopnia pierwszego.
Ćw.
Funkcja produkcji danego producenta jest funkcją typu Cobba-Douglasa postaci:
![]()
dla ![]()
gdzie K jest kapitałem a L siłą roboczą (pracą). Sformułować i rozwiązać zadanie maksymalizacji zysku tego producenta.
Drugie zadanie producenta (minimalizacja kosztów)
Załóżmy, że na danym rynku ukształtowały się ceny ![]()
(bo rozważamy model rynku konkurencyjnego). Załóżmy, że firma wytwarza jeden produkt w ilości y i jest zainteresowana minimalizacją kosztów tej wielkości produkcji.
Z matematycznego punktu widzenia zadanie to możemy zapisać w postaci:
![]()
.
Uwaga
Drugie zadanie przedsiębiorstwa jest zadaniem bliźniaczym do drugiego zadania konsumenta (minimalizacja wydatków przy zadanym poziomie użyteczności konsumenta).
Analogicznie jak w teorii wyboru konsumenta przy uczynionych założeniach o funkcji produkcji f mamy następujące twierdzenie o rozwiązaniu tego zadania.
Twierdzenie
Jeśli są spełnione podstawowe założenia o funkcji produkcji (![]()
, rosnąca, ściśle wklęsła (hesjan określony ujemnie), wówczas istnieje jedyny wektor ![]()
, który jest rozwiązaniem drugiego zadania producenta wtedy i tylko wtedy, gdy istnieje ![]()
taka, że para ![]()
spełnia układ równań:
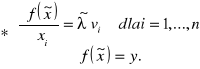
Uwaga
Układ równań (*) nosi nazwę układu warunków Lagranger'a dla ekstremum warunkowego jakim jest drugie zadanie producenta.
Ilustracja graficzna dla przypadku dwuwymiarowego
Z graficznego punktu widzenia zadanie to polega na wyznaczeniu takiego zestawu czynników produkcji ![]()
, aby prosta minimalnych kosztów osiągnęła izokwantę poziomu produkcji y (krzywa tego samego poziomu produkcji). Z uczynionych założeń o funkcji produkcji (wklęsłość) wnosimy, że izokwanty są wypukłe.
Uwaga
a) Z ostatniego twierdzenia wynika, że przedsiębiorstwo minimalizuje koszty wytwarzania ustalonej wielkości produkcji y, gdy angażuje taką ilość czynników produkcji, że krańcowa produkcyjność każdego z tych czynników produkcji jest proporcjonalna do jego ceny (vi jest ceną i-tego czynnika produkcji).
b) Z układu (*) widać również, że krańcowa stopa technicznej substytucji i-tego czynnika przez j-ty czynnik jest równa ilorazowi cen tych czynników, tzn.
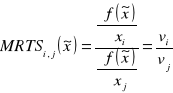
dla i, j=1,…,n.
Def. (funkcji warunkowego popytu na czynniki produkcji)
Funkcję ![]()
taką, że ![]()
nazywamy funkcją warunkowego popytu na czynniki produkcji.
Funkcja ta parze (v,y) przyporządkowuje najtańszą kombinację czynników produkcji na poziomie y przy wektorze cen czynników produkcji v ( jest to odpowiednik funkcji popytu Hicksa w teorii wyboru konsumenta).
Def. (funkcja kosztów produkcji)
Funkcję ![]()
, że parze ![]()
nazywamy funkcją (minimalnego) kosztu produkcji. Funkcja kosztów produkcji jest odpowiednikiem funkcji wydatków konsumenta.
Trzecie zadanie producenta
Modelujemy wydatki przedsiębiorstwa na rynku konkurencyjnym, a to oznacza, że do cen czynników produkcji przedsiębiorstwo musi dostosować poziom swojej produkcji. Stąd naturalną jest rzeczą, że najistotniejszym parametrem wyznaczającym koszty produkcji, na który ma wpływ firma jest jej poziom produkcji y, to pozwala patrzeć na koszty firmy jako na funkcję wielkości jej produkcji. Przedsiębiorstwo musi dostosować poziom swojej produkcji do zastanych cen na rynku. Stąd naturalną jest rzeczą, że najistotniejszym parametrem wyznaczającym zysk, na który ma wpływ firma jest jej poziom produkcji y. Takie podejście pozwala patrzeć na koszty firmy jako na funkcję tylko jej wielkości produkcji. Przy założeniu, że firma produkuje po kosztach minimalnych.
Przy takich założeniach możemy rozważać uproszczone zadanie maksymalizacji zysku tzn. wyznaczyć taki poziom produkcji ![]()
, który gwarantuje maksymalizację funkcji zysku firmy postaci
![]()
gdzie funkcja ![]()
jest minimalnym kosztem produkcji na poziomie y.
Twierdzenie
Przy założeniu, że funkcja kosztu c jest różniczkowalna i ściśle wypukła oraz spełnia warunek ![]()
wówczas funkcja zysku jest ściśle wklęsła i zadanie to ma dokładnie jedno optymalne rozwiązanie ![]()
, które spełnia warunek ![]()
Uwaga
Z ekonomicznego punktu widzenia warunek ![]()
oznacza, że koszt krańcowy optymalnej produkcji jest równy cenie produktu tzn. w przybliżeniu koszt wyprodukowania dodatkowej jednostki produktu przy danym poziomie produkcji jest równy cenie. Przedsiębiorstwu tak długo opłaca się zwiększać produkcję dopóki przychód krańcowy (przychód ze sprzedaży dodatkowo wyprodukowanej jednostki - równy jego cenie) jest większy od kosztu krańcowego (kosztu wytwarzania dodatkowej jednostki).
Obszar <y1,y2> to obszar opłacalnej produkcji.
Poziom produkcji yT jest poziomem o najniższym koszcie (tzw. optimum technologiczne). Jednak w modelu czystej konkurencji optimum technologiczne nie jest istotne a istotne jest optimum ekonomiczne (zrównanie kosztu krańcowego z ceną) odpowiada to poziomowi produkcji yE.
W modelu konkurencji doskonałej konsumenci zgłaszają popyt na dane dobra (krzywa popytu - zależność między ceną a ilością), a producenci zgłaszają swoją podaż danego dobra (krzywa podaży - zależność między ceną a ilością). W zdecydowanej większości przypadków krzywe te mają następującą postać (pomijamy poziomy nasycenia i możliwości technologiczne):
Rozwiązując powyższe równanie otrzymujemy cenę równowagi p*. Cena równowagi zapewnia optymalny wybór zarówno dla konsumentów jak i producentów.
y* - podaż i popyt w równowadze
Nadwyżka konsumenta odzwierciedla tę część dobrobytu społecznego, który pozostaje „w kieszeni” bogatszych konsumentów przy niższej cenie.
Nadwyżka producenta odzwierciedla tę część dobrobytu społecznego, który trafia do tych producentów, którzy produkują taniej niż wynikałoby to z ceny równowagi.
Ćw.
Funkcja produkcji danego producenta jest funkcją typu Cobba-Douglasa postaci:
![]()
gdzie K jest kapitałem a L siłą roboczą (pracą). Sformułować i rozwiązać drugie i trzecie zadanie producenta dla tej funkcji produkcji.
7
x
y
y=p f(x)
y=v x
x*
D
Cena p1 to popyt y1
Cena spada do p2, popyt rośnie do y2
y
p
p1
p2
y1
y2
Krzywa popytu D
Krzywa podaży S
y2
y1
p1
p2
p
y
Cena rośnie,
rośnie produkcja
S
f(x1, x2)=y izokwanta dla poziomu produkcji y
![]()
Wyszukiwarka
Podobne podstrony:
zachowanie się cieczy na gruncie
15. Teoria racjonalnego zachowania się konsumenta na rynku usług medycznych, licencjat(1)
15. Teoria racjonalnego zachowania się konsumenta na rynku usług medycznych(1)
Analiza zachowań nabywców na rynku konsoli popr (1)
6484, Turystyka i rekreacja wykłady, Zachowanie konsumentów na rynku usług turystycznych
Pytania na egzamin z BMZ, Studia UG, Psychologia, Semestr 1, Biologiczne mechanizmy zachowania się l
zachowania konsumentów na rynku turystycznym dr NIEMCZYK
Analiza zachowań nabywców na rynku konsoli
153627Promocja, Turystyka i rekreacja wykłady, Zachowanie konsumentów na rynku usług turystycznych
111032GPLAN MARKETINGOWY, Turystyka i rekreacja wykłady, Zachowanie konsumentów na rynku usług turys
133740praca do abrama2, Turystyka i rekreacja wykłady, Zachowanie konsumentów na rynku usług turysty
Plan strategiczno-marketingowy praca, Turystyka i rekreacja wykłady, Zachowanie konsumentów na rynku
GWSH - Teoria zachowania konsumentów, ZACHOWANIE, ZACHOWANIE KONSUMENTÓW NA RYNKU USŁUG TURYSTYCZNYC
Wykład 1 zachowanie konsumentów na rynku usług tur
Ankieta dotycząca zachowań konsumentów na rynku turystycznym
Wykład 3 zachowanie konsumentów na rynku usług tur GWSH
Zachowania nabywców na rynku E23SPHYWCLO5SMFA3FAQ7IJSK43LDBDW2QKMD3Y
więcej podobnych podstron