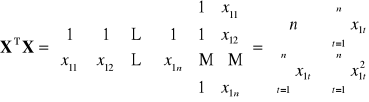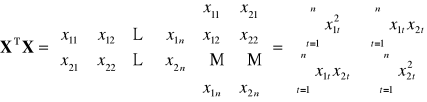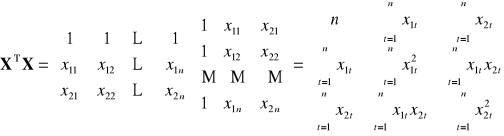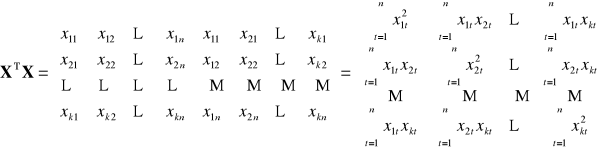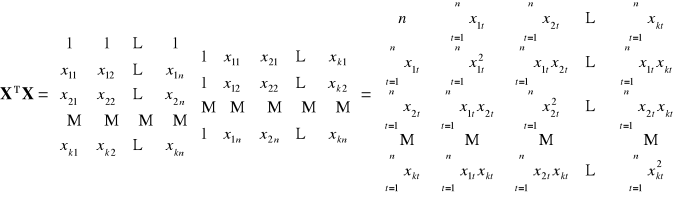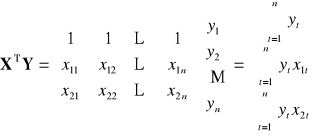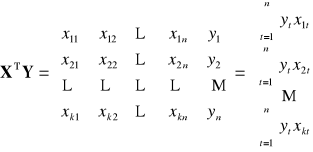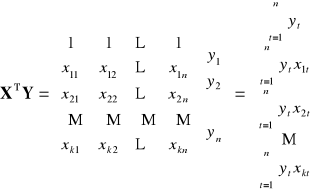I. MATEMATYKA
1. Potęgi o wykładnikach całkowitych.
Przez ![]()
, gdzie n jest liczba naturalną, rozumiemy iloczyn n czynników, z których każdy równa a się tzn. ![]()
; ![]()
.
n razy
Przyjmuje się, że każda liczba różna od zera poniesiona do potęgi zerowej równa się jeden, tzn.: ![]()
przy ![]()
.
Przez potęgę o wykładniku całkowitym ujemnym ![]()
, przy ![]()
, n - naturalnym, rozumiemy odwrotność ![]()
tzn. ![]()
.
Dla potęg o wykładnikach całkowitych przy założeniu, że![]()
, oraz![]()
, mamy następujące wzory:
(1.1.) ![]()
(1.4.) 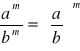
(1.2.) ![]()
(1.5.) ![]()
(1.3.) ![]()
2. Potęgi o wykładnikach wymiernych. Pierwiastki.
Niech a oznacza liczbę dodatnią, m i n - liczby naturalne; wówczas przez wyrażenie ![]()
(potęga o wykładniku wymiernym) rozumiemy pierwiastek arytmetyczny ![]()
. Dla ![]()
i ![]()
, ![]()
. Dla ![]()
oraz n naturalnym i nieparzystym otrzymujemy ![]()
. Zakłada się, że ![]()
.
(1.6.) ![]()
, dla ![]()
, ![]()
3. Funkcje wykładnicze.
Przez funkcję wykładniczą rozumiemy funkcję, która dowolnej liczbie rzeczywistej x przyporządkowuje liczbę ![]()
, ![]()
.
Najbardziej znaną funkcją wykładniczą jest funkcja ![]()
o podstawie ![]()
.
4. Funkcje logarytmiczne.
Niech a będzie liczbą dodatnia różną od 1, b zaś liczbą dodatnią. Przez logarytm b przy podstawie a, oznaczany symbolem ![]()
, rozumiemy taką liczbę c, która spełnia równość ![]()
.
Prawdziwe są następujące równości:
(1.7.) ![]()
(1.11.) ![]()
(1.8.) ![]()
, przy ![]()
, ![]()
i ![]()
(1.12.) ![]()
(1.9.) ![]()
(1.13.) ![]()
(1.10.) ![]()
METODA NAJMNIEJSZYCH KWADRATÓW - MNK
Założenia metody najmniejszych kwadratów
Liczebność próby n jest większa niż liczba szacowanych parametrów k, tj.
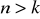
.Model musi być liniowy względem parametrów.
Pomiędzy wektorami obserwacji zmiennych objaśniających nie istnieje zależność liniowa. (jest to założenie o braku współliniowości). Rząd macierzy
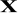
jest równy liczbie szacowanych parametrów.Zmienne objaśniające są nielosowe, ich wartości są traktowane jako wielkości stałe w powtarzających się próbach.
Wartości oczekiwane składników losowych są równe zeru, tzn.
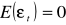
, dla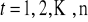
.Wariancje składników losowych
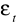
są stałe, tzn.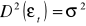
dla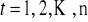
. Jest to tzw. homoskedastyczność.Składniki losowe
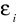
i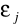
są od siebie niezależne, dla
,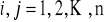
. Nie występuje autokorelacja składników losowych, tzn. współczynnik autokorelacji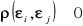
Każdy ze składników losowych
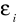
ma rozkład normalny.
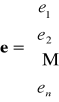
lub ![]()
- wektor reszt modelu, gdzie ![]()
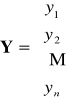
lub ![]()
- wektor obserwacji zmiennej objaśnianej
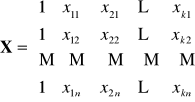
oraz 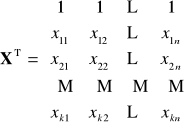
-
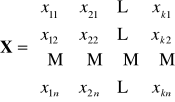
oraz 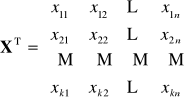
-
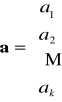
- 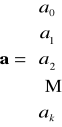
-
![]()
|
|
|
|
Dowolna (k-ta) ilość zmiennych objaśniających
|
Dowolna (k-ta) ilość zmiennych objaśniających
|
|
|
|
|
Dowolna (k-ta) ilość zmiennych objaśniających
|
Dowolna (k-ta) ilość zmiennych objaśniających
|
II. WERYFIKACJA STATYSTYCZNA MODELU EKONOMETRYCZNEGO
1. Wariancja składnika resztowego ![]()
(jako estymator wariancji składnika losowego) dana wzorem:
(2.1.) ![]()
, lub wzór macierzowy
(2.2.) ![]()
Warto zauważyć, że ![]()
; natomiast ![]()
, co znacznie ułatwi obliczenia.
2. Odchylenie standardowe reszt ![]()
(2.3.) ![]()
Wielkość ![]()
wskazuje na przeciętną różnicę między zaobserwowanymi wartościami zmiennej objaśnianej ![]()
i wartościami teoretycznymi ![]()
. Odchylenie standardowe reszt jest wielkością mianowaną; posiada takie samo miano jak zmienna objaśniana.
3. Macierz wariancji i kowariancji estymatorów parametrów
(2.4.) ![]()
Szczególne znaczenie maja elementy diagonalne tej macierzy (wariacje estymatorów parametrów). Pierwiastki z nich to błędy średnie szacunku parametrów. Natomiast poza główną przekątną znajdują się kowariancje estymatorów parametrów. A zatem:
(2.5.) ![]()
- wariancja estymatora parametru ![]()
(2.6.) ![]()
- kowariancja estymatorów ![]()
, ![]()
gdzie: ![]()
- element macierzy ![]()
jeśli ![]()
to wówczas ![]()
- będzie oznaczać element głównej przekątnej macierzy ![]()
Średni błąd estymatora
(2.7.) ![]()
, oznaczany często jako ![]()
Przedział ufności dla parametrów ![]()
(2.8.) ![]()
gdzie: ![]()
- wartość krytyczna dla zmiennej losowej o rozkładzie t-Studenta dla ![]()
stopni swobody, przy ustalonym z góry poziomie istotności ![]()
; np.: ![]()
; ![]()
, itp.
Interpretacja: z prawdopodobieństwem równym ![]()
, (np. 0,95) możemy twierdzić, że przedział określony wzorem (2.8.) pokryje faktyczną wartość szacowanego parametru ![]()
.
Miary dopasowania modelu do zmiennych empirycznych.
Ogólna suma kwadratów odchyleń wartości empirycznych zmiennej objaśnianej od wartości średniej, czyli całkowita zmienność zmiennej objaśnianej:
(2.9.) ![]()
gdzie:
![]()
- suma kwadratów odchyleń wartości teoretycznych zmiennej objaśnianej od wartości średniej, zmienność wyjaśniona (objaśniona) przez model.
![]()
- suma kwadratów reszt, czyli zmienność niewyjaśniona (objaśniona) przez model (zmienność resztowa).
Słownie wzór (2.9.) można przedstawić jako:
całkowita zmienność zmiennej objaśnianej |
= |
zmienność wyjaśniona |
+ |
zmienność niewyjaśniona |
Po podzieleniu wzoru (2.9.) obustronnie przez ![]()
, otrzymujemy:
(2.10.) 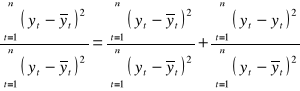
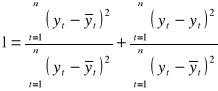
Oznaczając przez ![]()
zmienność wyjaśnioną przez model oraz przez ![]()
zmienność niewyjaśnioną przez model ostatecznie otrzymujemy
(2.11.) ![]()
4. Współczynnik determinacji ![]()
:
(2.12.) 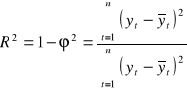
(2.13.) 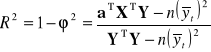
5. Współczynnik zbieżności ![]()
(2.14.) 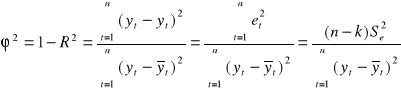
lub wzór macierzowy
(2.15.) 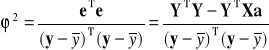
Interpretacja: zgodnie z przyjętymi oznaczeniami (2.9. - 2.11.) wiadomo, że zarówno współczynnik determinacji ![]()
jak i współczynnik zbieżności ![]()
przyjmują wartości z przedziału [0; 1]. Dopasowanie modelu do danych jest tym lepsze im współczynnik determinacji ![]()
jest bliski 1, oraz jeśli współczynnik zbieżności ![]()
jest bliski 0. Słabe dopasowanie modelu można stwierdzić po wartości współczynnika determinacji ![]()
bliskiego 0, oraz gdy współczynnik zbieżności ![]()
jest bliski 1. Zgodnie z tym współczynniki ![]()
i ![]()
są jednocześnie albo dobre, albo złe. Np. jeśli ![]()
to ![]()
, co oznacza, że model w 98% opisuje badane zjawisko, pozostałe 2% nie zostało objaśnione przez model - jest to zmienność odchyleń losowych.
Najczęstszymi przyczynami słabego dopasowania modelu są:
nieodpowiedni dobór zmiennych objaśniających,
niewłaściwa postać analityczna modelu.
(Warto powiedzieć, że w niektórych badaniach ekonometrycznych wartość ![]()
jest bardzo niska, co wynika z charakteru badanego zjawiska).
Innymi, często stosowanymi miernikami dopasowania modelu do danych empirycznych są:
6. Skorygowany współczynnik determinacji ![]()
:
(2.16.) ![]()
Jest to współczynnik determinacji ![]()
skorygowany stopniami swobody. Współczynnik ten pozwala porównywać dopasowanie równań różniących się ilością włączonych do nich zmiennych objaśniających.
7. Współczynnik korelacji wielorakiej ![]()
:
(2.17.) ![]()
Współczynnik korelacji wielorakiej ![]()
jest miarą siły związku liniowego zmiennej objaśnianej ![]()
ze zmiennymi objaśniającymi ![]()
.
Aby stwierdzić, czy dopasowanie modelu do danych empirycznych jest dostatecznie duże, można zweryfikować hipotezę o istotności współczynnika korelacji wielorakiej.
![]()
![]()
Sprawdzianem tej hipotezy jest następująca statystyka:
![]()
, gdzie: n - liczebność próby, k - liczba szacowanych parametrów.
Statystyka ta ma rozkład F Fishera-Snedecora o ![]()
oraz ![]()
stopniach swobody. Z tablic testu F dla zadanego poziomu istotności ![]()
odczytujemy wartość krytyczną ![]()
. Jeśli ![]()
to nie ma podstaw do odrzucenia hipotezy ![]()
, co oznacza, że współczynnik korelacji wielorakiej jest nieistotny. Jeśli ![]()
, to odrzucamy hipotezę ![]()
, co oznacza, że współczynnik ![]()
jest istotny.
8. Współczynnik zmienności losowej ![]()
, zwany inaczej współczynnikiem wyrazistości:
(2.18.) ![]()
Współczynnik ten informuje o tym, jaką część średniej wartości zmiennej objaśnianej stanowi jej odchylenie standardowe. W praktyce zależy nam, aby wartość ![]()
była możliwie bliska 0. dlatego też przyjmuje się w danym badaniu pewna wartość krytyczną ![]()
(np. ![]()
=0,1). Jeżeli ![]()
, to przyjmuje się, że model jest dopuszczalny.
Testowanie hipotez dotyczących istotności parametrów
9. Test t-Studenta o istotności parametrów strukturalnych modelu.
Za pomocą tego testu badamy istotność poszczególnych parametrów pojedynczo.
![]()
![]()
Sprawdzianem tej hipotezy jest test oparty na statystyce t-Studenta:
(2.19.) 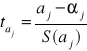
lub wykorzystując inne oznaczenie 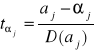
gdzie:
![]()
- ocena j-tego parametru,
![]()
- prawdziwa wartość parametru (zgodnie z hipotezą zerową ![]()
),
![]()
- błąd średni szacunku parametru ![]()
.
W związku z powyższym wzór (2.19.) przyjmuje ostatecznie postać:
(2.20.) 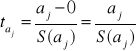
Po odczytaniu z tablic rozkładu t-Studenta, wartości krytycznej ![]()
, dla przyjętego poziomu sitotności ![]()
oraz ![]()
(gdzie k - oznacza liczbę szacowanych parametrów) stopni sowbody, sprawdzamy czy ![]()
. Jeśli tak to należy odrzucić hipotezę zerową ![]()
na korzyść hipotezy alternatywnej![]()
. A zatem parametr ![]()
istotnie różni się od zera. W przeciwnym wypadku, tzn. gdy ![]()
nie podstaw do odrzucenia hipotezy ![]()
, co oznacza, że parametr ![]()
jest nieistotny statystycznie.
Uwaga!!!
Przy zapisie oszacowanego modelu stosowane są trzy konwencje zapisu:
I ![]()
(1,82) (0,79) (0,11) - w nawiasach podano średnie błedy szacunku parametrów ![]()
Zgodnie ze wzorem (2.20.), otrzymujemy:
![]()
![]()
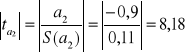
(lub -8,18)
dla ![]()
wszystkie relacje ![]()
są spełnione, zatem wszystkie parametry strukturalne są istotne.
II ![]()
(14,29) (6,08) (-8,18) - w nawiasach podano wartości testu t-Studenta dla poszczególnych parametrów
III ![]()
(14,29) (6,08) (8,18) - w nawiasach podano wartości bezwzględne testu t-Studenta dla poszczególnych parametrów
Należy zwrócić na to szczególną uwagę. Najpierw trzeba się zorientować, co oznaczają liczby w nawiasach a dopiero potem zastanowić się czy należy dzielić oszacowania parametrów przez ich średnie błędy szacunku (tak jak w I przypadku), czy też od razu przystąpić do interpretacji (tak jak w przypadku II i III). Wykonanie dzielenia z przypadku I i zastosowanie tej reguły w II (III) przypadku prowadzi do fałszywych wniosków: ![]()
![]()
![]()
co wskazuje, że wszystkie parametry są niestotne. Informacja o tym co oznaczają liczby w nawiasch musi być podana, inaczej nie można dokonać interpretacji, czy parametry strukturalne modelu są istotne czy też nie.
10. Test F Fishera-Snedecora o istotności parametrów strukturalnych modelu.
Test F jednocześnie testuje cały układ współczynników regresji (najczęściej bez wyrazu wolnego); inaczej jak w teście t-Studenta, gdzie testowano parametry osobno:
![]()
Hipoteza alternatywna![]()
jest taka, że co najmniej jedna z równości nie jest spełniona, Sprawdzianem hipotezy ![]()
jest:
(2.21.) 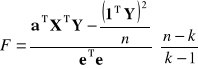
gdzie:
![]()
- jest n-elementowym wektorem „jedynek”, zatem ![]()
Podobnie jak w 7. statystyka ta ma rozkład F Fishera-Snedecora o ![]()
oraz ![]()
stopniach swobody. Z tablic testu F dla zadanego poziomu istotności ![]()
odczytujemy wartość krytyczną ![]()
. Jeśli ![]()
to nie ma podstaw do odrzucenia hipotezy ![]()
, co oznacza, że współczynniki regresji są nieistotne. Jeśli ![]()
, to odrzucamy hipotezę ![]()
, co oznacza, że współczynniki regresji są statystycznie istotne.
Warto powiedzieć, że w przypadku 7, 9, 10 oznaczenie wartości krytycznej jest dowolne, tzn. można dodać do litery oznaczającej odpowiedni test indeks dolny ![]()
(poziom istotności) lub e - oznaczający „empiryczny”, „*” lub inne oznaczenie, wyraźnie wskazując w opisie czego dotyczy dany symbol i w konsekwencji co oznacza podana wartość.
11. Test DW Durbina-Watsona o występowaniu autokorelacji reszt.
Badanie autokorelacji składników losowych sprowadza się do badania autokorelacji reszt. Do tego celu, służy test Durbina-Watsona DW.
Najpierw sprawdza się, jaki jest współczynnik autokorelacji reszt I rzędu, określony wzorem:
(2.22.) 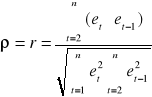
![]()
- litera alfabetu greckiego „ro”, lub łacińskie „r”
gdzie:
![]()
- reszty modelu
![]()
- reszty opóźnione o jeden okres
a następnie sprawdzamy testem DW następującą hipotezę ![]()
:
![]()
![]()
lub ![]()
(2.23.) 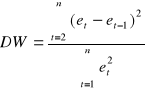
, często test DW oznacz się przez ![]()
Rozkład DW przyjmuje wartości od 0 do 4 i jest symetryczny. W związku z tym jest on ztablicowany od 0 do 2. Jeśli zatem wartość DW obliczona za pomocą wzoru (2.23.) jest większa od 2, np. 2,32 to należy dokonać prostego przekształcenia polegającego na odjęciu od 4 wartości DW.
(2.24.) ![]()
w naszym przykładzie: ![]()
Obliczoną wartość DW czy ![]()
porównujemy z dwoma wartościami krytycznymi:
![]()
L-Lower i ![]()
U-Upper
Interpretacja:
I. ![]()
w modelu występuje autokorelacja reszt
II ![]()
test DW nie daje odpowiedzi na pytanie czy w w modelu występuje autoko-
relacja reszt.
III ![]()
w modelu nie występuje autokorelacja reszt
I II III
![]()
![]()
![]()
ŹLE ??? DOBRZE
Opracowanie mgr Markos Jeropulos na podstawie:
Gajda J.B. - „Ekonometria praktyczna”, Absolwent Łódź, 2002
Jajuga K. (red.) - „Ekonometria. Metody i analiza problemów ekonomicznych”, Wydawnictwo Akademii Ekonomicznej we Wrocławiu, Wrocław, 2002.
Krzysztofiak M. (red.) - „Ekonometria”, PWE, Warszawa 1978.
Kukuła K. (red.) - „Wprowadzenie do ekonometrii w przykładach i zadaniach”, PWN, Warszawa 1999.
Łapińska-Sobczak N. (red.) - „Opisowe modele ekonometryczne”, Wydawnictwo Uniwersytetu Łódzkiego, Łódź, 2001.
Nowak E. - „Zarys metod ekonometrii”, PWN, Warszawa 2002.
9
macierz obserwacji
zmiennych objaśniających
![]()
z wyrazem wolnym ![]()
macierz obserwacji
zmiennych objaśniających
![]()
bez wyrazu wolnego
Wektor ocen parametrów
z wyrazem wolnym
Wektor ocen parametrów
bez wyrazu wolnego
Wyszukiwarka
Podobne podstrony:
Modele jednorównaniowe
elektrorafinacja miedzi wersja koncowa
konspekt wersja ostateczna, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki mate
Wersja końcowa
konspekt wersja nowa
Raport z wyszukiwania - wersja końcowa, Studia INiB, Projekty profesjonalne 1
lista lekow ANS CVS wersja końcowa, medycyna UMed Łódź, 3 rok, farmakologia, kolokwium 2
KURS MŁODSZY RATOWNIK 2007 wersja końcowa
modele jednorAXAXwnaniowe
transport kopalniany wersja koncowa
prezentacja chloroplasty moja wersja koncowa
Przemoc w mediach prezentacja wersja koncowa 2
sfg wersja koncowa
TESCO wersja koncowa
konspekt temat i koncowka rzeczownika, obocznosciZ
sprawko5 wersja końcowa
sprawko 1 wersja końcowa popr popr
KSIĘGI PROROCKIE (wersja końcowa), Teologia(3)
Sprawozdanie TRANS wersja końcowa
więcej podobnych podstron