POZIOMY ENERGETYCZNE ATOMU WODORU. STAŁA RYDBERGA
Opracowanie wyników.
Do sprawdzenia optymalnego ustawienia spektrometru użyłem rurki helowej. W poniższej tabelce zestawiałem dane tablicowe z danymi uzyskanymi w doświadczeniu. Dane te użyje do sprawdzenia krzywej cechowania osi x programu obsługi spektrometru, wykorzystując pomiar długości fali helu.
DŁUGOŚĆ FALI λ [nm] |
|
Wartość tablicowa |
Wartość zmierzona |
388,8 |
386,6 |
447,2 |
446,2 |
501,6 |
501,5 |
587,6 |
588,0 |
667,8 |
668,3 |
706,5 |
707,2 |
728,1 |
729,0 |
∆λ=3nm
Rysuję wykres zależności długości fali rzeczywistej od podawanej przez program. Metodą najmniejszych kwadratów poprowadziłem prostą przez punkty znajdujące się na wykresie. Pomiary długości fali mierzonej dla wodoru skoryguje według wzoru:
![]()
Tablicowa długość fali λ [nm] |
Czas ekspozycji [ms] |
Średnia długość fali λ [nm] |
λ po poprawce [nm] |
1/λ [1/nm] |
n |
1/n² |
|||
|
350 |
1000 |
2000 |
3000 |
|
|
|
|
|
434,05 |
- |
432,8 |
433,2 |
432,7 |
432,9 |
434,10 |
0,0023036 |
5 |
0,04 |
486,13 |
486,9 |
486,7 |
486,0 |
486,8 |
486,6 |
487,38 |
0,0020518 |
4 |
0,0625 |
456,28 |
658,4 |
658,2 |
658,3 |
658,3 |
658,3 |
657,74 |
0,0015204 |
3 |
0,1111 |
![]()
=2,9766
n-jest główną liczbą kwantową czyli powłoką, z której elektron przechodzi na drugą powłokę.
Obliczam błąd odwrotności długości fali, korzystając z prawa przenoszenia błędów:
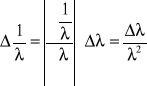
|
0,0000158 |
0,0000125 |
0,0000069 |
Rysuję wykres zależności odwrotności długości fali λ od odwrotności kwadratu n.
Stałą Rydberga wyznaczam ze wzoru:
![]()
gdzie R to stała Rydberga, którą mam wyznaczyć, natomiast n wynoszą: 5, 4, 3.
n |
R [1/m] |
5 |
10969666,91 |
4 |
10942895,65 |
3 |
10946585,39 |
Stała Rydberga wynosi (wartość średnia):
R=10953049,25
Obliczam niepewność otrzymanej wartości korzystając z metody przenoszenia błędów:
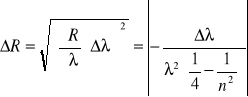
gdzie:
∆λ=3nm
n |
∆R [1/m] |
5 |
75810,16 |
4 |
67357,67 |
3 |
49928,22 |
Błąd wyznaczenia stałej Rydberga (wartość średnia) wynosi:
∆R=64365,35
Ostateczny wynik:
R=10953049,25 ± 64365,35 [1/m]
Uzyskany wynik nie różni się znacznie od rzeczywistego, który wynosi: R=10967757,6 [1/m],
więc będę go używał do dalszych obliczeń.
Energię jonizacji obliczę przekształcając wyrażenie:
![]()
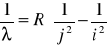
gdzie i, j są numerami powłok, pomiędzy którymi przechodzi elektron (z j na i). Wstawiając za j=1, i =∞ (gdyż energia jonizacji atomu wodoru odpowiada energii związanej z przeniesieniem elektronu z pierwszego poziomu energetycznego na zewnątrz atomu) oraz korzystając z zależności:
otrzymuję:
![]()
gdzie:
E - szukana energia jonizacji;
h - stała Planca -h=6,626![]()
![]()
;
c - prędkość światła -c= 299793 [km/s];
E=2,18![]()
[V] =13,59 [eV] (e=1,602![]()
[C])
Obliczam błąd wyznaczenia energii jonizacji (zależy on jedynie od błędu wyliczonej wcześniej stałej Rydberga, gdyż pozostałe zmienne są stałymi tablicowymi) korzystając ze wzoru:
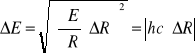
∆E=1,28![]()
[V] = 0,08 [eV]
Ostatecznie otrzymujemy:
E=13,59 ± 0,08 [eV]
Otrzymane wyniki nieznacznie odbiegają od wyników tablicowych, co świadczy o poprawnym przeprowadzeniu doświadczenia. Niedokładność mierzonych wielkości wynika jedynie z dokładności wykonywania pomiarów przez aparaturę, która wynosiła 3 nm. Przy wyznaczaniu odwrotności długości fali pozostawiłem wiele liczb znaczących ze względu na rząd wyznaczonego błędu, a więc dokładności otrzymanych po zaokrągleniu wyników. Jedynie błąd wyznaczenia stałej Rydberga jest niepokojąco duży. Jako przyczynę takiego stanu rzeczy uważam przeliczanie na metry pomiarów wykonanych w nanometrach (program dokonuje pewnych zaokrągleń).
![]()
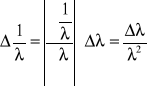
![]()
![]()
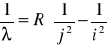
![]()
![]()
Wyszukiwarka
Podobne podstrony:
rys, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 11 Poziomy energetyc
Nr ćwiczenia 11, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 11 Pozio
Poziomy energetyczne atomu wodoru. Stała Rydberga, Elektrotechnika AGH, Semestr II letni 2012-2013,
poziomy energetyczne atomu wodoru, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Labo
Lepkość-sciaga, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
mostek Wheatstone'a(1), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
za, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
więcej podobnych podstron