ZWIĄZKI KOMPLEKSOWE
podstawy dla licealistów
Opracował: mgr Jarosław Kot
|
|
strona |
1. |
Znaczenie związków kompleksowych................................. |
......2 |
2. |
Budowa związków kompleksowych.................................... |
......3 |
3. |
Liczba koordynacyjna.......................................................... |
......4 |
4. |
Przestrzenna budowa kompleksów....................................... |
......4 |
5. |
Nazwy kompleksów............................................................. |
......5 |
6. |
Wzory kompleksów.............................................................. |
......5 |
7. |
Tworzenie kompleksów........................................................ |
......7 |
8. |
Kompleksy wielordzeniowe................................................. |
......7 |
9. |
Kompleksy chelatowe.......................................................... |
......8 |
10. |
Roztwory kompleksów......................................................... |
......8 |
11. |
Trwałość kompleksów.......................................................... |
......9 |
12. |
Doświadczenia...................................................................... |
....10 |
13. |
Zadania................................................................................. |
....12 |
14. |
Literatura.............................................................................. |
....13 |
1. Znaczenie związków kompleksowych.
„Związki koordynacyjne mają ogromne i stale wzrastające znaczenie w wielu dziedzinach technologii i techniki. Znajdują zastosowanie w analizie chemicznej, w procesach wymiany jonowej, w przemyśle syntezy chemii nieorganicznej i organicznej. Wykorzystanie różnego rodzaju atomów centralnych (praktycznie cała tablica Mendelejewa ze szczególnym uwzględnieniem metali d-elektronowych) i różnorodnych ligandów (w tym ogromna liczba ligandów organicznych) umożliwia otrzymywanie wręcz nieograniczonej liczby związków kompleksowych o różnorodnych i specyficznych właściwościach.
Związki koordynacyjne odgrywają istotną rolę w funkcjonowaniu organizmów żywych, jak np. barwniki oddechowe (np. hemoglobina, mioglobina) jako układy przenoszące elektrony (cytochromy), układy biorące udział w fotosyntezie (chlorofil), jako metalo-enzymy pośredniczące w metabolizmie białek (kompleksy metali z peptydami i kwasami nukleinowymi).”
dr Maria A. Kanas, Uniwersytet Jagielloński
„Okazuje się jednak, że związków kompleksowych jest o wiele więcej niż pozostałych związków nieorganicznych. Duża liczba kompleksów wynika stąd, że liczne metale mogą tworzyć wiązania koordynacyjne, a różnych ligandów też jest wiele. (...)
Wśród kompleksów znajdują się związki o niezwykłych właściwościach chemicznych i biologicznych i o różnych zastosowaniach. Dlatego chemia związków kompleksowych jest najszybciej rozwijającym się działem chemii. Przyroda też znalazła zastosowania dla tych związków. Kompleksem, na który najczęściej patrzymy jest chlorofil, zielony barwnik liści. Cząsteczka chlorofilu zawiera kation Mg(II), połączony wiązaniami koordynacyjnymi z czterema atomami azotu, które należą do bardzo dużej cząsteczki organicznej.”
prof. dr hab. Przemysław Mastalerz
W programie szkolnym związki kompleksowe pojawiają się przy okazji realizacji różnych zagadnień. Na przykład:
1. Amfoteryczne właściwości wodorotlenków i tlenków niektórych metali, np.:
Al(OH)3 + KOH → K[Al(OH)4] tetrahydroksoglinian(III) potasu
K[Al(OH)4] → K+ + [Al(OH)4]− anion tetrahydroksoglinioanowy(III)
K[Al(OH)4] ![]()
K[Al(O)2] + 2 H2O dioksoglinian(III) potasu
(tradycyjnie: metaglinian potasu KAlO2)
K[Al(O)2] → K+ + [Al(O)2]− anion dioksoglinianowy(III)
2. Odczynnik Tollensa - amoniakalny roztwór wodorotlenku srebra:
AgOH + 2 NH3 → [Ag(NH3)2]OH wodorotlenek diaminasrebra(I)
[Ag(NH3)2]OH → [Ag(NH3)2]+ + OH− kation diaminasrebra(I)
3. Procesy fotograficzne - utrwalanie materiałów światłoczułych:
AgBr (klisza) + 2 Na2S2O3 (utrwalacz) → Na3[Ag(S2O3)2] + NaBr
ditiosiarczanosrebrzan(I) sodu
Na3[Ag(S2O3)2] → 3 Na+ + [Ag(S2O3)2]3- anion ditiosiarczanosrebrzanowy(I)
4. Rozpuszczanie złota w wodzie królewskiej (mieszanina 1 cz. HNO3 + 3 cz. HCl)
tworzy się kompleks: H[AuCl4] kwas tetrachlorozłotowy(III)
H[AuCl4] → H+ + [AuCl4]− anion tetrachlorozłotowy(III)
5. Wykrywanie alkoholu wielowodorotlenowego:
H
CH2 -OH CH2 -O O −H
+ Cu(OH)2 → Cu dihydroksoglikolomiedź(II)
CH2 -OH CH2 -O O −H
H
lub raczej:
CH2 -OH CH2-O O-CH2
2 + CuSO4 + 2 NaOH → Na2 Cu + H2SO4 + 2 H2O
CH2 -OH CH2-O O-CH2
diglikolomiedzian(II) sodu
(według: dr M. A. Kanas, UJ)
2. Budowa związków kompleksowych.
Określenie: „kompleks” odnosi się do cząsteczek lub jonów, w których z atomem >A< związane są inne atomy >B< lub grupy atomów >C< w liczbie (zwykle) przewyższającej wartościowość atomu >A<.
Atom >A< nazywany jest „rdzeniem” lub „atomem centralnym”.
Atomy >B< lub grupy >C< nazywane są „ligandami”.
Cały zespół jednego lub kilku atomów centralnych i związanych z nimi ligandów nazywa się „jednostką koordynacyjną” lub „kompleksem”.
Kompleks może być:
1) kationem
np.: [Cr(H2O)6]3+ kation h e k s a a k w a c h r o m u (III)
[Al(OH)(H2O)5]2+ kation p e n t a a k w a h y d r o k s o g l i n u (III)
2) anionem
np.: [Fe(CN)6]3- anion h e k s a c y j a n o ż e l a z i a n o w y (III)
(tradycyjnie nazywany: anion żelazocyjankowy)
[Fe(CN)6]4- anion h e k s a c y j a n o ż e l a z i a n o w y (II)
(tradycyjnie nazywany: anion żelazicyjankowy)
3) obojętną cząsteczką
np.: [Co(NO2)3(NH3)3] t r i a m i n a t r i n i t r o k o b a l t (III)
[Fe(CO)5] p e n t a k a r b o n y l ż e l a z o (0)
3. Liczba koordynacyjna.
Każdy atom centralny ma charakterystyczną „liczbę koordynacji” („liczbę koordynacyjną”) czyli tzw. „ligandowość”, która jest liczbą atomów bezpośrednio z nim związanych.
W najczęściej spotykanych kompleksach liczba koordynacyjna (LK) jest następująca:
jeżeli centralny jest atom metalu jednowartościowego, to zwykle LK = 2 np. [Ag(CN)2]-
jeżeli centralny jest atom metalu dwuwartościowego, to zwykle LK = 4 np. [Cu(NH3)4]2+
jeżeli centralny jest atom metalu trójwartościowego, to zwykle LK = 6 np. [Al(H2O)6]3+
4. Przestrzenna budowa kompleksów.
W przypadku najprostszych kompleksów:
jeżeli LK = 2, to struktura przyjmuje kształt liniowy:
L O L
jeżeli LK = 4, to kompleks przyjmuje kształt płaskiego kwadratu lub czworościanu:
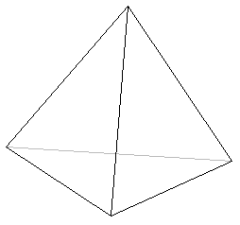
L L
lub
L L
jeżeli LK = 6, to kształt bipiramidy tetragonalnej czyli ośmiościanu:
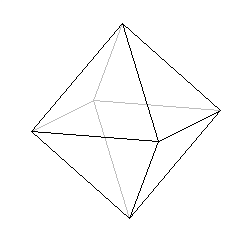
5. Wzory kompleksów.
We wzorach kompleksów umieszcza się:
jako pierwszy symbol pierwiastka atomu centralnego,
w drugiej kolejności wymienia się (symbolami lub wzorami) jonowe ligandy,
następnie ligandy neutralne.
Wzór całego kompleksu zamyka się w nawiasy kwadratowe.
Jeżeli w skład kompleksu wchodzi większa ilość ligandów i to w różnych klasach (kationowe, anionowe, obojętne), to kolejność w każdej klasie ligandów powinna być alfabetyczna wg. symboli pierwiastków, których atomy związane są bezpośrednio z atomem centralnym.
Przykłady wzorów kompleksów:
[CoCl(NH3)5]2+ atom centralny: Co (dokładnie: Co3+);
ligand jonowy: Cl− ;
ligand obojętny: NH3
[Fe(CN)5CO]2− atom centralny: Fe (dokładnie: Fe3+);
ligand jonowy: CN− ;
ligand obojętny: CO
[Co(CN)(CO)2 (NO)] − atom centralny: Co (na zerowym stopniu utlenienia);
ligand jonowy: CN− ;
ligandy obojętne: CO i NO (alfabetycznie: C przed N)
6. Nazwy kompleksów.
W nazwach kompleksów:
nazwę pierwiastka stanowiącego atom centralny umieszcza się za nazwami ligandów wymienionych alfabetycznie;
stosuje się liczebniki: di, tri, tetra, penta, heksa itd. jeżeli ligand występuje odpowiednio dwu-, trzy-, cztero-, pięcio- lub sześciokrotnie w danym kompleksie;
nazwy ligandów tworzy się następująco:
a) cząsteczki obojętne nazywa się następująco:
H2O akwa NH3 amina
CO karbonyl NO nitrozyl
b) nazwę liganda anionowego tworzy się dodając na końcu literę „o”, do nazwy soli
zawierającej taki anion:
![]()
siarczano („siarczan” + „o”)
S2O32- tiosiarczano („tiosiarczan” + „o”)
![]()
wodorosiarczano („wodorosiarczan” + „o”)
C2O42− szczawiano („szczawian” + „o”)
C4H6O42− winiano („winian” + „o”)
podobnie:
C6H5− fenylo („fenyl” + „o”)
stosuje się także nazwy:
OH− hydrokso Cl− chloro
CN− cyjano O2− okso
SCN− tiocyjaniano S2− tio
(tradycyjnie: rodano) H− hydrydo
NO2− nitro
(azotyno, azotano(III))
c) ligandy kationowe występują niezmiernie rzadko, w nietypowych przypadkach
Przykłady nazw kompleksów:
kation pentaaminachlorokobaltu(III)
w nazwie tej:
liczebnik „penta”,
kolejność nazw ligandów alfabetyczna: „amina” przed „chloro”,
atom centralny: kobalt(III) tzn. Co3+,
końcówka nazwy w dopełniaczu według ogólniejszej reguły budowania nazw kationów (kation czego?);
anion pentacyjanokarbonylożelazianowy(III)
w nazwie tej:
liczebnik „penta”,
kolejność alfabetyczna nazw ligandów: „cyjano” przed „karbonyl”(łącznik gramatyczny „o”),
atom centralny: żelazo(III) tzn. Fe3+
końcówka „-owy” według ogólniejszej reguły budowania nazw anionów
(anion jaki? np.. „azot” - „azotanowy”, więc „żelazo” - „żelazianowy”)
anion cyjanodikarbonylonitrozylokobaltanowy(0)
w nazwie tej:
.......................... (uzupełnij samodzielnie)
7. Tworzenie kompleksów.
Kompleksy powstają ze związków prostych, w wyniku przyłączenia jonów lub cząsteczek obecnych w środowisku reakcji, do atomów (metali) w innym związku. Połączenie następuje na zasadzie tworzenia wiązań koordynacyjnych (tj. donorowo-akceptorowych), dzięki obecności wolnych par elektronowych w wiążącym atomie liganda - ten atom liganda jest donorem, a atom centralny (metal), w pierwotnym związku prostym jest akceptorem pary elektronowej tworzącej nowe wiązanie.
Tendencję do tworzenia kompleksów wykazują głównie metale grup pobocznych tj. bloku d.
Przykłady:
chrom |
(Cr) |
[Cr(NH3)6]3+ |
[Cr(OH)4]- |
[Cr(OH)6]3- |
mangan |
(Mn) |
[Mn(CN)6]3- |
[Mn(CN)6]4- |
[Mn(CN)6]5- |
żelazo |
(Fe) |
[Fe(CN)6]3- |
[Fe(CN)6]4- |
[FeF6]3+ |
kobalt |
(Co) |
[Co(NH3)6]3+ |
[Co(NH3)4(H2O)2]3+ |
[Co(NO2)4(NH3)]- |
nikiel |
(Ni) |
[Ni(NH3)4]2+ |
[Ni(CO)4] |
[Ni(H2O)6]2+ |
miedź |
(Cu) |
[Cu(NH3)4]2+ |
[Cu(CN)2 ]- |
[CuCl2(H2O)2] |
srebro |
(Ag) |
[Ag(NH3)2]+ |
[Ag(CN)2]- |
[Ag(S2O3)2]2- |
złoto |
(Au) |
[Au(CN)4]- |
[AuCl4]- |
|
cynk |
(Zn) |
[Zn(OH)4]- |
[Zn(NH3)4]2+ |
|
kadm |
(Cd) |
[CdCl6]4- |
|
|
rtęć |
(Hg) |
[HgCl4]2- |
|
|
platyna |
(Pt) |
[PtCl6]2- |
[PtCl3(NH3)3] |
|
i inne.
Kompleksy tworzą także niektóre metale grup głównych (bloku p lub także s):
glin |
(Al) |
[Al(OH)4]- |
[Al(OH)6]3- |
[Al(OH)2(H2O)4]+ |
beryl |
(Be) |
[Be(OH)4]2- |
|
|
cyna |
(Sn) |
[Sn(OH)3]- |
|
|
ołów |
(Pb) |
[Pb(OH)3]- |
|
|
arsen |
(As) |
[As(OH)4]- |
|
|
i inne.
8. Kompleksy wielordzeniowe.
Niektóre kompleksy zawierają kilka atomów centralnych.
Są to tak zwane „związki wielordzeniowe”.
Przykłady:
[(NH3)5Co(OH)Co(NH3)5]5+ kation μ-hydroso-bis[pentaaminakobaltu(III)]
[(CO)3Fe(CO)3Fe(CO)3] tri-μ-karbonyl-bis(trikarbonylżelazo)
i wiele innych, o dużo bardziej złożonej strukturze.
9. Kompleksy chelatowe.
Niektóre cząsteczki, zawierające więcej niż jedną, wolną parę elektronów, mogą wiązać się z atomem centralnym więcej niż jednym wiązaniem koordynacyjnym. Takie ligandy nazywane są „chelatowymi” lub „kleszczowymi”, a związki takie nazywa się „chelatami”, „związkami chelatowymi” lub „związkami kleszczowymi”.
Na przykład EDTA czyli kwas etylenodiaminatetraoctowy (skrót od nazwy angielskiej), nazwywany także „kwasem wersenowym”. Związek ten (oraz jego sole - „werseniany”) znajduje bardzo istotne zastosowanie w analityce chemicznej. Strukturę tej substancji można przedstawić następująco:
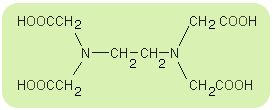
Związek ten tworzy chelatowe struktury kompleksowe jako ligand:
- sześciokleszczowy: 2 x para elektronów przy atomie azotu oraz
4 x para elektronów przy atomie tlenu z grupy -OH,
- dwukleszczowy: tylko 2 x para elektronów przy atomie azotu.
10. Roztwory kompleksów.
Wiele kompleksów o charakterze soli dobrze rozpuszcza się w wodzie (często lepiej niż proste sole, z których kompleks powstaje). W roztworze wodnym związki takie dysocjują na jony kompleksowe. Takie, złożone jony zwykle są bardzo trwałe.
Roztwory związków kompleksowych, tj. zawierające jony kompleksowe, mają często wyraźną, charakterystyczną barwę.
Przykłady:
[Co(NH3)6]Cl3 ![]()
[Co(NH3)6]3+ + 3 Cl- roztwór o barwie żółtej
[CoCl(NH3)5]Cl2 ![]()
[CoCl(NH3)5]2+ + 2 Cl- roztwór o barwie purpurowoczerwonej
[Cu(H2O)4]Cl2 ![]()
[Cu(H2O)4]2+ + Cl- roztwór o barwie niebieskiej
11. Trwałość kompleksów.
Struktury kompleksowe tj. związki lub jony w roztworach wodnych na ogół dysocjują tylko w nieznacznym stopniu.
Na przykład proces:
[Ag(CN)2]- ⇄ Ag+ + CN-
przebiega tylko ze znikomo małą wydajnością co oznacza, że praktycznie nie ma w roztworze jonów Ag+ i CN-.
Reakcję tworzenia kompleksu można przedstawić schematycznie:
M + n L ⇄ MLn
M - atom centralny (metal) L - ligand MLn - kompleks
Jest to proces równowagowy, podlega prawu działania mas i stąd stała równowagi reakcji tworzenia kompleksu, nazywana „stałą trwałości”:
K1 = β = ![]()
Dla reakcji odwrotnej tj. rozpadu (dysocjacji) kompleksu:
MLn ⇄ M + n L
definiuje się „stałą nietrwałości”:
K2 = ![]()
= 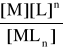
Stałe te charakteryzują każdy kompleks. Na przykład im wartość stałej nietrwałości jest mniejsza, tym trwalszy jest kompleks.
W praktyce podaje się wartość stałej nietrwałości kompleksu w formie:
pK2 = − log10(K2) = − log10(![]()
)
im większa jest wartość pK2, tym trwalszy jest kompleks.
W trakcie tworzenia się kompleksów następuje często podstawianie jednych ligandów innymi tj. o mniejszej stałej nietrwałości. Tworzą się w ten sposób kompleksy trwalsze.
Przykład:
[Ag(NH3)2]+ K2 = ![]()
= 9,3⋅10-8 pK2 = 7,03
[Ag(S2O3)2]3- K2 = ![]()
= 3,5⋅10-14 pK2 = 13,46
oznacza to, że po wprowadzeniu jonów tiosiarczanowych do amoniakalnego roztworu jonów srebra utworzy się tiosiarczanokompleks srebra.
12. Doświadczenia.
(1)
Do bezbarwnego roztworu azotanu(V) srebra dodawać małymi porcjami bezbarwny roztwór zawierający jony chlorkowe (np. NaCl).
Wytrąca się biały, kłaczkowaty osad chlorku srebra.
Następnie dodawać stężony, wodny roztwór amoniaku.
Osad całkowicie się rozpuszcza. Powstaje bezbarwny, klarowny roztwór w wyniku tworzenia się kompleksu [Ag(NH3)2]+.
Podobne doświadczenie można wykonać dodając na wstępie roztwór NaOH i wytrącając brązowy osad wodorotlenku srebra, a następnie rozpuszczając ten osad w amoniaku.
AgNO3 + NaCl → AgCl↓ + NaNO3
Ag+ + Cl- → AgCl↓
AgCl + 2 NH3 → [Ag(NH3)2]+ + Cl-
Reakcje takie mają znaczenie analityczne przy rozpoznawaniu osadów związków srebra.
(2)
Do niebieskiego roztworu soli miedzi(II) (np. CuCl2) dodawać małymi porcjami stężony, wodny roztwór amoniaku.
Początkowo wytrąca się żelowaty, niebieski (lub niebieskozielony) osad wodorotlenku miedzi(II).
Wobec nadmiaru amoniaku osad rozpuszcza się i powstaje ciemnoniebieski roztwór.
Niebieska barwa początkowego roztworu pochodzi od kompleksowych akwajonów [Cu(H2O)4]2+. Charakterystyczna, ciemnoniebieska barwa końcowego roztworu świadczy o obecności aminajonów [Cu(NH3)4]2+.
Cu2+ + 2 OH− → Cu(OH)2 ↓
Cu(OH)2 + 4 NH3 → [Cu(NH3)4]2+ + 2 OH−
Reakcja taka ma znaczenie analityczne przy wykrywaniu obecności nawet nieznacznych ilości jonów miedzi(II) w roztworze. Aminakompleks tworzy się bardzo łatwo, reakcja ta jest bardzo czuła, a ciemnoniebieska barwa jest bardzo wyraźna nawet przy niewielkich ilościach kompleksu.
(3)
Do zielonego roztworu soli niklu(II) (np. NiSO4) dodawać małymi porcjami stężony, wodny roztwór amoniaku.
Początkowo wytrąca się żelowaty, bladozielony osad wodorotlenku niklu(II).
Wobec stopniowo rosnącego nadmiaru amoniaku osad rozpuszcza się i powstaje roztwór o barwie najpierw niebieskiej, a potem niebieskofioletowej.
Zielona barwa początkowego roztworu pochodzi od kompleksowych akwajonów [Ni(H2O)6]2+. Stopniowo następuje wymiana cząsteczek wody w strukturze kompleksu na cząsteczki amoniaku. Towarzyszy temu zmiana barwy roztworu.
Ni2+ + 2 OH− → Ni(OH)2 ↓
Ni(OH)2 + m NH3 + n H2O → [Ni(NH3)m(H2O)n]2+ + 2 OH−
[Ni(NH3)m(H2O)n]2+ + n NH3 → [Ni(NH3)6]2+ + n H2O
gdzie, w kolejnych etapach:
m = 1, 2, 3, 4, 5 n = 5, 4, 3, 2, 1, 0
(4)
Do zielononiebieskiego (morskiego) roztworu soli chromu(III) (np. Cr2(SO4)3 ) dodawać powoli, małymi porcjami stężony, wodny roztwór amoniaku.
Początkowo wytrąca się zielonoszary, żelowaty osad wodorotlenku chromu(III).
Wobec nadmiaru amoniaku osad rozpuszcza się i powstaje zielony roztwór, który następnie zmienia barwę na kolor żółty.
Następnie dodawać powoli, małymi porcjami roztwór zawierający jony chlorkowe (np. NaCl) w umiarkowanym stężeniu.
Barwa roztworu zmienia się na kolor purpurowy, następnie na zielony, potem na fioletowy i wreszcie na pomarańczowoczerwony.
Zielononiebieska (morska) barwa początkowego roztworu pochodzi od akwajonów [Cr(H2O)6]3+.
Po rozpuszczeniu osadu w nadmiarze amoniaku powstają aminajony [Cr(NH3)6]3+, a przejściowa, widoczna przez chwilę zielona barwa roztworu pochodzi od hydroksojonów [Cr(OH)6]3-.
Dalej, w trakcie stopniowo rosnącego stężenia jonów chlorkowych następuje stopniowa wymiana cząsteczek amoniaku, w strukturze kompleksu, na jony Cl-.
Tworzą się kolejno kompleksowe struktury:
[CrCl(NH3)5]2+, [CrCl2(NH3)4]+, [CrCl3(NH3)3], [CrCl4(NH3)2]-
czemu towarzyszy odpowiednia zmiana barwy roztworu.
(5)
Do żółtego roztworu soli żelaza(III) (np. FeCl3) dodawać małymi porcjami niezbyt stężony roztwór rodanku czyli tiocyjanianu (np. KSCN).
W miarę rosnącego stężenia jonów rodanowych (tiocyjanianowych) SCN- pojawia się czerwone zabarwienie.
Żółte zabarwienie początkowego roztworu pochodzi od akwajonów [Fe(H2O)6]3+.
Ciemniejące, czerwone zabarwienie pojawia się w miarę tworzenia się kompleksów z udziałem liganda rodanowego (tiocyjanianowego), podczas stopniowej wymiany cząsteczek wody na aniony rodankowe (tiocyjanianowe).
Powstaje struktura kompleksowa o zmiennym składzie:
[Fe(SCN)m(H2O)n]x gdzie w kolejnych etapach:
m = 1, 2, 3, 4, 5, 6
n = 5, 4, 3, 2, 1, 0
a ładunek zmienia się odpowiednio: x = +2, +1, 0, -2, -3
Reakcja ta ma znaczenie analityczne. Stosowana jest do oznaczania zawartości jonów żelaza(III) w roztworze. Rodankowe kompleksy żelaza(III) tworzą się bardzo łatwo, reakcja jest bardzo czuła, a barwa roztworu jest bardzo wyraźna.
13. Zadania.
Sformułuj nazwy kompleksów: anionowych, kationowych, obojętnych, których wzory podano w niniejszym opracowaniu.
Zapisz wzory i podaj nazwy soli potasowych zawierających aniony kompleksowe oraz wodorotlenków zawierających kompleksowe kationy wykorzystując przykłady jonowych kompleksów podanych w niniejszym opracowaniu.
Napisz wzory kompleksów, których wzory podano w niniejszym opracowaniu.
Napisz równania kolejnych reakcji przeprowadzonych w doświadczeniu (4) i w (5).
Określ stopnie utlenienia pierwiastków w podanych kompleksach.
Zapisz równanie reakcji tworzenia kompleksu (kompleksowania), którego stała trwałości opisana jest zależnością:
β = 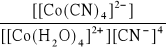
Zapisz wyrażenie opisujące stałą nietrwałości (

) kompleksu powstającego w reakcji:
[Cu(H2O)4]2+ + 2 Br− ⇄ [CuBr2(H2O)2]
14. Literatura.
[1] „Chemia ogólna i nieorganiczna. Podręcznik 1. Liceum (...)” B. Kałuża i inni,
Żak WE Zofii Dobkowskiej, W-wa 2003, Wyd. I, str. 81-82
[2] „Chemia. Podręcznik i zbiór zadań w jednym. Liceum(...)” R. Hassa i inni,
Wyd. M. Rożak, Gdańsk 2002, Wyd. I, rozdz: IV.5 „Związki kompleksowe”
[3] „Chemia dla szkół średnich w testach. Część 2.” A. Persona i inni, WSiP, W-wa 1998,
Wyd. I, rozdz: 16.1 „Związki kompleksowe (zespolone, koordynacyjne)”.
[4] „Chemia. Wybór testów z egzaminów wstępnych na akademie medyczne i kierunki
przyrodnicze. Tom 1.Chemia ogólna.” A. Persona, MEDYK, W-wa 2000, Wyd. IV,
rozdz: 21 „Związki kompleksowe”.
[5] „Szkolny poradnik chemiczny” Z. Dobkowska, K. M. Pazdro, WSiP, W-wa 1990,
Wyd. II, str. 60 „Struktura kompleksów”, 94 „Tworzenie związków kompleksowych”,
324 „Związki kompleksowe”.
[6] „Nowe nazewnictwo w chemii - związków nieorganicznych i organicznych” W. Śliwa i
inni, WSiP, W-wa 1994, Wyd. I, rozdz: „Związki koordynacyjne”.
[7] „Nomenklatura związków nieorganicznych” PTChem, OSSOLINEUM Wyd. PAN, W-w,
W-wa, K-ów, Gdańsk, Łódź, 1988, Wyd. I, rozdz: 7 „Związki koordynacyjne”.
[8] „Tablice chemiczne” W. Mizerski, Wyd. ADAMANTAN, W-wa 1997, Wyd. II, rozdz:
„Nazewnictwo chemiczne” str. 308 - 311 „Związki koordynacyjne”.
[9] „Tablice chemiczne” J. Sawicka i inni, Wyd. PODKOWA, Gdańsk 2001, Wyd. I, rozdz:
„Sole. Związki kompleksowe”.
[10] „Związki kompleksowe w programach szkół średnich” M. A. Kanas, Czasopismo
„Niedziałki”, Fundacja „PRO CHEMIA” Wydz. Chemii UJ, Nr 2/98(25), K-ów.
[11] „Zadania i ćwiczenia z chemii ogólnej.” N. Glinka, PWN, W-wa 1973, Wyd. 11,
rozdz: XIII „Związki kompleksowe”.
[12] „Elementarna chemia nieorganiczna” P. Mastalerz, Wyd. Chemiczne D. Mastalerz,
W-w 1997, Wyd. I, rozdz: 6.4 „Najważniejsze pierwiastki z bloku d. Kompleksowe
związki chromu.” str. 231 - 234.
[13] „Chemia ogólna i nieorganiczna” A. Bielański, PWN, W-wa 1977, Wyd. V,
rozdz: 10 „Związki kompleksowe”.
[14] „Chemia” L. Pauling, P. Pauling, PWN, W-wa 1983, Wyd. I, rozdz: 16 „Kompleksy
nieorganiczne i związki koordynacyjne”.
[15] „Chemia analityczna” J. Dobrowolski, Państ. Zakł. Wyd. Lekar., W-wa 1976, Wyd IV.
rozdz: 1.4 „Związki kompleksowe”.
[16] „Chemia analityczna z elementami analizy instrumentalnej.” T. Lipiec, Z. Szmal, Państ.
Zakł. Wyd. Lekar., W-wa 1976, Wyd. IV, rozdz: 2.3 „Związki kompleksowe”.
1
8.1. Roztwory zawierające związki kompleksowe. Stała trwałości
kompleksu.
W praktyce chemicznej oprocz kwasow, zasad i soli prostych często mamy do czynienia ze
związkami złoŜonymi. Najprostsza definicja związku kompleksowego mowi o związku w
ktorym z atomem centralnym (ktorym jest zwykle jon lub atom metalu) związane są ligandy
w liczbie przekraczającej klasyczną wartościowość. Przykładowo: stały jodek rtęci(II) dodany
do roztworu jodku potasu roztwarza się w nim i tworzy się rozpuszczalny w wodzie
tetrajodortęcian(II) potasu:
HgI2(s) + 2KI(aq) = K2HgI4(aq)
Podobnie AgCl moŜna przeprowadzić do roztworu uŜywając amoniaku:
AgCl(s) + 2 NH3(aq) = Ag(NH3)2Cl(aq)
Powstałe związki w wyniku dysocjacji elektrolitycznej nie ulegają rozpadowi na jony proste,
lecz na jony kompleksowe, np.:
K2HgI4(aq) => 2 K+(aq) + HgI4
2-(aq)
Ag(NH3)2Cl(aq) => Ag(NH3)2
+ (aq) + Cl-(aq)
Jony HgI4
2- są na tyle trwałe, Ŝe prostymi metodami nie stwierdzimy obecności jonow Hg2+ i
I- (właściwie jonow uwodnionych Hg2+(aq) i I-(aq)). Jako proces kompleksowania będziemy
uwaŜać reakcję przebiegającą między jonami prostymi z utworzeniem jonu kompleksowego:
Hg2+ + 4 I- <=> HgI4
2-
i załoŜymy, Ŝe jony potasu nie biorą udziału w reakcji. Pojawiają się tutaj pytania. Jak
nazywać powstające związki kompleksowe (nomenklatura)? Czy moŜna przewidzieć, ile
ligandow danego rodzaju będzie się wiązało z atomem danego metalu? Z czego wynika
trwałość tych związkow? Czy reakcja tworzenia kompleksu zachodzi do końca, czy teŜ
częściowo i otrzymujemy stan rownowagi między produktami i substratami? W obecnym
opracowaniu zajmiemy się szczegołowo tylko tym ostatnim zagadnieniem.
Większość reakcji kompleksowania zachodzi w sposob rownowagowy, do osiągnięcia stanu,
w ktorym szybkość powstawania substratow rowna się szybkości tworzenia produktow.
PoniewaŜ dochodzenie do rownowagi jest procesem wymagającym czasu, w chemii
związkow kompleksowych oprocz pojęcia: związek trwały/ nietrwały (stabilny/niestabilny)
mamy do czynienia z rozgraniczeniem pod względem szybkości tworzenia i rozpadu. Tak
więc związki, ktore ulegają bardzo wolno rozkładowi (choć mogą być energetycznie mało
stabilne) nazywamy kompleksami inertnymi, natomiast związki ulegające szybkim procesom
tworzenia i rozpadu nazywamy labilnymi (mogą być termodynamicznie trwałe, tzn. mieć duŜe
stałe trwałości).
Stan rownowagi tworzenia związku kompleksowego ilościowo oddaje stała trwałości, ktora
zwyczajowo najczęściej oznaczana jest grecką literą (beta). Tak więc dla procesu tworzenia
związku o wzorze ogolnym MLn (M- metal, L-ligand, n-liczba ligandow) mamy następujący
wzor na termodynamiczną stałą rownowagi:
M + nL = MLn
n
M L
n
n ML
n
M L
T ML
M L f f
ML f
a a
a
n n
[ ][ ]
[ ]
Wartość tego ilorazu jest stała dla danej temperatury i dla danej reakcji. Dla siły jonowej
roztworu I= . (Cizi
2) rownej zero i dla bardzo rozcieńczonych roztworow wspołczynniki
aktywności rownają się jeden i wowczas moŜna stałą termodynamiczną zastąpić stałą
stęŜeniową. W innych przypadkach stała stęŜeniowa przyjmuje stałą wartość w danej
temperaturze pod warunkiem stałości siły jonowej roztworu
2
n
n
M L
ML
[ ][ ]
[ ] (I=const)
Aby przeliczyć termodynamiczne stałe trwałości (a takie stałe są najczęściej umieszczane w
tablicach) na stałe stęŜeniowe (warunkowe, dla określonej siły jonowej) naleŜy uŜyć
wspołczynnikow aktywności.
T = [MLn]fMLn /([M]fM [L]n fL
n) = fMLn fM -1fL
-n [MLn]/([M][L]n)
Tak więc:
= T fMLn
-1fM fL
n
NaleŜy dodać, Ŝe największa zmiana wspołczynnikow aktywności następuje przy przejściu od
stęŜeń bliskich zeru do stęŜeń umiarkowanych, powiedzmy 0,05. Dalsza zmiana
wspołczynnikow aktywności w zakresie I=0,05 do I=0,3 jest zwykle mniejsza.
Dla naszych celow będziemy uŜywać następującego uproszczenia. Stałych
termodynamicznych będziemy uŜywać dla roztworow trudnorozpuszczalnych osadow w
wodzie, a stałych warunkowych wynikających z interpolacji danych z tabeli dla siły jonowej
wynikającej z warunkow zadania. W przypadkach, gdy końcowa siła jonowa jest trudna do
przewidzenia, przyjmować będziemy stałą dla I=0,1M.
Jeśli rozwaŜamy proces dysocjacji tego samego kompleksu na składniki, zamiast stałą
trwałości moŜna posługiwać się stałą nietrwałości, ktora jest odwrotnością stałej trwałości.
MLn = M + n L
[ ]
1 [ ][ ]
n
n
ML
M L
K
Bilans metalu w roztworze, w ktorym wspołistnieją jony metalu oraz kilka kompleksow ML1 ,
ML2 , MLn itp. moŜna opisać rownaniem (przyjmując 0=1):
CM = [M] + [ML] + [ML2] + [ML3] + ... = i
i
i [M] [L]
Przykład.
Obliczyć stęŜenia jonow Ag+ oraz SCN- obecne w 0,05M roztworze K[Ag(SCN)2].
Rozwiązanie.
Po pierwsze z tabeli stałych trwałości musimy wybrać stałą odpowiednią do występującej siły
jonowej. Musimy ją obliczyć. Siła jonowa będzie wynikała przede wszystkim z dysocjacji
związku według rownania K[Ag(SCN)2] → K+ + Ag(SCN)2
-. PoniewaŜ jest to elektrolit 1-1
siła jonowa rowna się stęŜeniu kompleksu I=c=0,05. Odczytujemy log = 8,76, czyli
=108,76= 5,754・108.
Teraz moŜemy zająć się dysocjacją komplekowego anionu na składniki:
Ag(SCN)2
- <=> Ag+ + 2 SCN-
start 0,05 0 0
rown. 0,05-x x 2x
Wstawiamy te wartości do wzoru na stałą trwałości kompleksu
2 2 3
2
4
0,05
(2 )
0,05
[ ][ ]
[ ( ) ]
x x x
x
Ag SCN
Ag SCN ≈
−
−
−
Po prostym przekształceniu mamy:
3
4
0,05
x = 2,79・10-4.
3
Otrzymana wartość x potwierdza słuszność naszego załoŜenia, Ŝe 0,05 - x ≈ 0,05.
Zgodnie z schematem podanym poniŜej rownania reakcji mamy więc
[Ag+] = x = 2,79・10-4 M; [SCN-] = 2x = 5,58・10-4 M.
8.2. Równowagi w układach zawierających związki trudnorozpuszczalne.
Iloczyn rozpuszczalności. Wpływ składu roztworu na rozpuszczalność
osadów.
Zjawisko rozpuszczania substancji stałych w wodzie (oraz innych cieczach) ma duŜe
znaczenie praktyczne. Początkowo, po dodaniu ciała stałego do wody i wymieszaniu
otrzymujemy roztwór nienasycony, tzn. taki w ktorym moŜna nadal rozpuścić substancję.
Inaczej sprawę ujmując roztwor nienasycony to taki, w ktorym nie ma rownowagi pomiędzy
ciałem stałym a cieczą, gdyŜ substancja moŜe się rozpuścić zwiększając stęŜenie w fazie
ciekłej. Stosując argumentację z poprzedniego podrozdziału powiemy, Ŝe szybkość
rozpuszczania jest większa niŜ szybkość krystalizowania substancji z roztworu. Kontynuując
dodawanie substancji do roztworu i mieszanie, dochodzimy do takiego układu, w ktorym
stęŜenie osiąga swoją maksymalną wartość (ktorej juŜ w danej temperaturze nie daje się
przekroczyć). Taki roztwor nazywamy roztworem nasyconym. Jest to stan, w ktorym faza
stała i ciekła znajdują się w rownowadze.
W przypadku substancji obojętnych elektrycznie - niejonowych - zwykle wystarcza nam
poznanie zaleŜności stęŜenia roztworu nasyconego od temperatury. Dla osadow substancji
nieorganicznych będących solami, zwykle na rozpuszczalność, oprocz temperatury, silnie
wpływa rownieŜ skład roztworu. Ma to znaczenie zwłaszcza, gdy interesujemy się
rozpuszczalnością nie tylko w czystej wodzie ale i w roztworach innych soli lub w roztworach
kwasow czy zasad.
Stałą rownowagi, ktora ustala się pomiędzy trudno rozpuszczalną solą a jej nasyconym
roztworem, nazywa się iloczynem rozpuszczalności. Zwykle zakłada się, Ŝe sole w
roztworach wodnych są całkowicie zdysocjowane na jony a jony te są w postaci uwodnionej
(zhydratowanej), co niekiedy zaznaczamy podając w nawiasie wskaźnik aq - aqueous).
Przykładowo dla procesu rozpuszczania Ag2SO4 w wodzie mamy rownowagę
Ag2SO4(s) <=> 2 Ag+(aq) + SO4
2-(aq)
Stąd wyraŜenie na stałą rownowagi (pomijamy fazę stałą oraz oznaczenia roztworu aq)
K= [Ag+]2 [SO4
2-]
Iloczyn rozpuszczalności jest to iloczyn stęŜeń molowych jonow, podniesionych do potęg,
będących wspołczynnikami stechiometrycznymi w rownaniu dysocjacji danej soli.
Wartość tego iloczynu jest stała w warunkach stałej temperatury i jest charakterystyczna dla
danej substancji i rozpuszczalnika. Zwroćmy uwagę na to, Ŝe stęŜenia molowe jonow w
powyŜszym wzorze dotyczą roztworu nasyconego - inaczej nie moŜna mowić o rownowadze
a tym samym nie ma sensu prowadzenie tego typu obliczeń.
WyraŜenie na termodynamiczną stałą rownowagi zawiera aktywności substancji zamiast
stęŜeń. Aktywność substancji dana jest jako iloczyn stęŜenia i wspołczynnika aktywności.
Dla reakcji rozpuszczania osadu o składzie AmBn danej ogolnym rownaniem:
AmBn(s) = m An+ + n Bm-
wyraŜenie na termodynamiczną stałą rownowagi Ka będzie miało postać:
Ka = aA
m ・ aB
n = [A]m ・ [B]n ・ fA
m ・ fB
n
gdzie:
aA aktywność jonu A, aA = [A]fA,
4
fA wspołczynnik aktywności jonu A (w zapisie pominięto ładunki jonow).
Wspołczynniki aktywności moŜna wyrazić jako funkcję siły jonowej I, zaleŜnej od stęŜeń i
ładunku wszystkich jonow obecnych w roztworze I= . (Cizi
2).
Stosowanie stałych stęŜeniowych zamiast stałych termodynamicznych ma sens dla silnie
rozcieńczonych roztworow, gdy wspołczynniki aktywności są bliskie jedynce i aktywności
moŜna zastąpić stęŜeniami. Wowczas K =Ka. Inny sposob na ominięcie tego problemu polega
na dodaniu duŜego nadmiaru elektrolitu podstawowego. (np. 0,1M roztwor NaClO4 jako tzw.
elektrolit podstawowy). JeŜeli stęŜenia innych substancji w roztworze są znacznie mniejsze,
to moŜna załoŜyć, Ŝe całkowita siła jonowa roztworu pozostaje stała i nie zmienia się na
skutek przebiegu badanej reakcji. Stałość siły jonowej zapewnia stałość wspołczynnikow
aktywności. Stałą, będącą iloczynem stałej termodynamicznej i wspołczynnikow aktywności,
nazywamy stałą warunkową K dla określonej wartości siły jonowej I.
K = Ka ・ fA
-m ・ fB
-n, (I= const)
Posługiwanie się taką stałą jest bardziej praktyczne, bo wszystkie niewiadome są w postaci
stęŜeń a nie aktywności. Aby moŜna było prowadzić obliczenia naleŜy z tablic odczytać
wartość iloczynu rozpuszczalności, bądź innej stałej fizykochemicznej, dla wstępnie
oszacowanej całkowitej siły jonowej roztworu.
Wyznaczanie iloczynu rozpuszczalności moŜe być trudne eksperymentalnie, gdyŜ z jednej
strony uzyskanie roztworu nasyconego z soli i wody moŜe być bardzo długotrwałe.
Otrzymywanie roztworu nasyconego poprzez sporządzenie stęŜonego roztworu w wyŜszej
temperaturze i ochładzanie z kolei moŜe prowadzić do dość trwałych roztworow
przesyconych. Dzieje się tak, poniewaŜ wytworzenie nowych kryształow fazy stałej wymaga
przejścia przez etap tworzenia zarodkow. Zbyt małe fragmenty nowej fazy są niestabilne
dopoki nie osiągną pewnej granicznej wielkości - wielkości zarodka, ktory juŜ jest zdolny do
samorzutnego wzrostu. W opisanych obliczeniach pomijamy te trudności natury technicznej
czy dotyczące szybkości dochodzenia do rownowagi i zajmujemy się obliczeniami stęŜeń
występujących w układach, w ktorych występuje rownowaga między osadem a roztworem
nasyconym.
ZaleŜność między rozpuszczalnością a iloczynem rozpuszczalności.
Iloczyn rozpuszczalności jest miarą rozpuszczania danego elektrolitu w wodzie. Mniejsza
wartość oznacza, Ŝe mniejsze są stęŜenia odpowiednich jonow w roztworze nasyconym.
Porownywanie bezpośrednie iloczynu rozpuszczalności dla kilku elektrolitow ma sens jedynie
w przypadku soli o jednakowej stechiometrii, tzn. mających analogiczny wzor chemiczny.
Tak więc, na podstawie znajomości iloczynow rozpuszczalności PbCl2 i PbI2 wynoszących
1,7・10-5 i 9,8・10-9 moŜemy wyciągnąć wniosek, Ŝe PbCl2 jest lepiej rozpuszczalny w wodzie.
Porownanie iloczynow rozpuszczalności AgCl i Ag2CrO4 rownych 1,77・10-10 i 1,12・10-12
mogłoby sugerować, Ŝe stęŜenie molowe nasyconego roztworu chromianu srebra jest
mniejsze, co nie jest zgodne z prawdą.
Aby iloczyn rozpuszczalności przeliczyć na rozpuszczalność wystarczy zastosować jego wzor
definicyjny, wynikający z rownania na dysocjację. Podobnie, na podstawie znajomości
stęŜenia molowego roztworu nasyconego z łatwością wyznaczymy iloczyn rozpuszczalności.
Przykład
Rozpuszczalność CaF2 w wodzie wynosi 2,0・10-4 mol/dm3. Oblicz iloczyn rozpuszczalności.
CaF2(s) <=> Ca2+ + 2 F-
IR(CaF2) = [Ca2+][F-]2
5
[Ca2+] = C
[F-]= 2・C
Stąd: IR(CaF2) = C (2・C)2 = 4 C3
Po podstawieniu wartości liczbowych otrzymujemy 3,2・10-11.
Odpowiedź: Iloczyn jonowy CaF2 wynosi 3,2・10-11. PoniewaŜ stęŜenia są małe jest on
praktycznie rowny stałej termodynamicznej, wynoszącej K(CaF2)=3,45・10-11.
Przykład
Iloczyn jonowy (dla I=0,01) CaSO4 wynosi 7,4・10-5 (termodynamiczny 3,14・10-5). Oblicz:
a) rozpuszczalność CaSO4 w wodzie (czyli stęŜenie roztworu nasyconego tego związku)
b) ile mg CaSO4 zawarte jest w 200 cm3 tego roztworu.
a) CaSO4(s) <=> Ca2+ + SO4
2-
IR(CaSO4) = [Ca2+][SO4
2-]
[Ca2+] = C, [SO4
2-] = C
IR(CaSO4) = C2
C I R
C = 0,0086 M
b) masa substancji - liczba moli razy masa molowa - m= nM= CVM
m = 0,0086 mol/dm3・0,200 dm3・136 g/mol = 0,234 g = 234 mg.
Odpowiedź: rozpuszczalność CaSO4 w wodzie wynosi 0,0086 M, a w 200 cm3 nasyconego
roztworu znajduje się 234 mg tej substancji.
Kryterium nasycenia roztworu elektrolitu
Roztwor substancji niejonowej w wodzie, ktory zawiera więcej substancji niŜ roztwor
nasycony (tzw. roztwor przesycony) dochodzi do rownowagi poprzez wydzielenie kryształow
ciała stałego, co powoduje zmniejszenie stęŜenia. JeŜeli stęŜenie jest mniejsze niŜ w
roztworze nasyconym a nie ma kryształow, ktore moŜna by rozpuścić, aby zwiększyć to
stęŜenie, to roztwor pozostaje nienasycony i nie ma tu rownowagi między fazą stałą a
roztworem.
Wiemy, Ŝe w stanie rownowagi iloczyn jonowy rowna się iloczynowi stęŜeń (podniesionych
do odpowiednich potęg) obecnych w roztworze nasyconym. Wartość iloczynu utworzonego
ze stęŜeń odpowiednich jonow moŜna wykorzystać do przewidywania, czy roztwor jest
nienasycony, czy nasycony. JeŜeli wartość tego iloczynu będzie większa od iloczynu
rozpuszczalności, to układ, aby dojść do rownowagi, musi zmniejszyć stęŜenia. Odbywa się
to poprzez utworzenie fazy stałej, wytrącenie osadu i usunięcie części jonow z roztworu. Z
kolei wartość iloczynu stęŜeń jonow mniejsza od iloczynu rozpuszczalności oznacza, Ŝe
mamy do czynienia z roztworem nienasyconym. W tym przypadku, aby dojść do stęŜeń
rownowagowych konieczne byłoby zwiększenie stęŜeń jonow np. przez rozpuszczenie dalszej
porcji ciała stałego.
Warunkiem aby osad mogł się wytrącić, jest aby iloczyn ze stęŜeń jonow elektrolitu w
roztworze, podniesionych do odpowiednich potęg, przekroczył wartość iloczynu
rozpuszczalności.
W przypadku substancji jonowej moŜemy mieć do czynienia z roztworem, w ktorym stęŜenia
jonow nie są w proporcji stechiometrycznej, lecz w proporcji wynikającej z ilości składnikow
dostarczonych przez eksperymentatora. W tej sytuacji, aby stwierdzić czy osad powstanie,
musimy zastosować kryterium podane powyŜej.
Bardzo waŜne jest, aby zwrocić uwagę na wzajemne rozcieńczenie roztworow. Oznacza to, Ŝe
stęŜenie reagentow (np. fosforanu sodu oraz chlorku wapnia w przykładzie poniŜej)
6
zmniejszy się po ich zmieszaniu w stosunku do stęŜeń początkowych. Jest to zrozumiałe,
poniewaŜ ta sama liczba moli substancji znajduje się w roztworze o większej objętości. Dla
celow praktycznych często moŜna załoŜyć, Ŝe objętość roztworu po zmieszaniu rowna się
sumie objętości roztworow wyjściowych, co oznacza zaniedbanie kontrakcji lub ekspansji
roztworow. Efekt ten jest zwykle mały, szczegolnie gdy mamy do czynienia z roztworami
rozcieńczonymi.
Przykład
Do 50 cm3 0,02 M roztworu CaCl2 dodano 150 cm3 0,1 M roztworu Na3PO4 i rozcieńczono
wodą do objętości 500 cm3. Obliczyć czy w tych warunkach wytrąci się osad Ca3(PO4)2.
IR(Ca3(PO4)2) = 4,0・10-30 (dla I=0,1). Zaniedbać wpływ siły jonowej.
Po pierwsze uwzględniamy wzajemne rozcieńczenie i liczymy bilansowe stęŜenia obu soli,
wykorzystując wzor C1V1 = C2V2:
C(CaCl2) = 0,02 M* 50 cm3 / 500 cm3 = 0,002 M
C(Na3PO4) = 0,1 M * 150 cm3 / 500 cm3 = 0,03 M
Z powodu sformułowania „dopełniono wodą do objętości 500 cm3” zjawisko kontrakcji nie
ma znaczenia, gdyŜ objętość końcowa jest podana dokładnie i nie musi być obliczana.
Napiszmy rownanie dysocjacji fosforanu wapnia i wynikający z niego wzor na iloczyn
rozpuszczalności.
Ca3(PO4)2 (s) = 3Ca2+ + 2 PO4
3-
IR(Ca3(PO4)2) = [Ca2+]3 [PO4
3-]2
Teraz liczymy iloczyn stęŜeń jonow wg wzoru danego przez iloczyn rozpuszczalności
[Ca2+] = C(CaCl2), [PO4
3-] = C(Na3PO4)
[Ca2+]3 [PO4
3-]2 = (0,002)3 (0,03)2 = 7,2・10-12
PoniewaŜ 7,2・10-12 > IR dochodzimy do wniosku, Ŝe osad się wytrąci. Spowoduje to
(jednoczesne) zmniejszenie stęŜeń jonow wapnia i jonow PO4
3- aŜ do uzyskania rownowagi,
czyli do uzyskania wartości zdefiniowanej przez iloczyn rozpuszczalności.
Uwaga: Wytrąceniu Ca3(PO4)2 towarzyszy powstanie NaCl, ktory pozostaje w roztworze i
wnosi swoj wkład do siły jonowej roztworu, oprocz obecności reagentow nadmiarowych. W
kaŜdym razie siła jonowa I w stanie rownowagi jest roŜna od zera. Mniejszy błąd popełniamy
uŜywając IR(Ca3(PO4)2) dla I=0,1 niŜ termodynamicznego iloczynu rozpuszczalności.
Pominiemy komplikacje związane z precyzyjnym uwzględnianiem faktycznej siły jonowej w
roztworze po wytrąceniu osadu.
Przykład
Do 100 cm3 roztworu zawierającego 0,001M AgNO3 dodano 10 cm3 nasyconego roztworu
PbBr2. Obliczyć, czy wytrąci się osad AgBr.
Wpływ siły jonowej zaniedbamy, gdyŜ stęŜenia są niewielkie i uŜyjemy stałych
termodynamicznych (dla I=0).
W pierwszym kroku liczymy stęŜenia występujące w nasyconym roztworze PbBr2.
PbBr2(s) = Pb2+ + 2Br-
IR(PbBr2) = [Pb2+][Br-]2
IR = C (2C)2 = 4 C3
C= 3
4
R I
= 3
6
4
6,6 10⋅ −
= 0,0118 M
czyli [Br-]nas. = 2C = 0,0236 M.
7
Teraz moŜemy policzyć bilansowe stęŜenia Ag+ i Br- wynikające z rozcieńczenia roztworow.
Stosujemy dwukrotnie wzor C1V1 = C2V2, zakładamy Ŝe (zaniedbujemy kontrakcję) objętość
końcowa roztworu będzie rownała się sumie objętości składnikow, czyli 110 cm3.
[Br-] = 0,0236M ・ 10 cm3/110 cm3 = 0,00215 M
[Ag+] = 0,001 M ・ 100 cm3/110 cm3 = 9,09・10-4 M.
Tworzymy iloczyn analogiczny do iloczynu rozpuszczalności AgBr
[Ag+] [Br-]= 2,15・10-3 ・9,09・10-4 = 1,953・10-6 > IR(AgBr) = 5,35・10-13
Jest to wartość większa od iloczynu rozpuszczalności AgBr, więc osad się wytrąci.
W ścisłym ujęciu powinniśmy się posłuŜyć warunkową stałą rownowagi wyznaczoną dla siły
jonowej wynikającej ze składu roztworu nad osadem. JeŜeli zastosowano nadmiar reagenta,
nie moŜna uznać siły jonowej za bliską zeru. Stosowanie do tych warunkow
termodynamicznego iloczynu rozpuszczalności (czyli słusznego dla I=0) moŜe prowadzić do
znacznych odstępstw teorii od praktyki, nawet rzędu kilkunastu - kilkudziesięciu procent. Z
tego powodu wyniki uzyskane na podstawie stałych termodynamicznych i stęŜeń molowych
naleŜy traktować jako pierwsze, zgrubne oszacowanie. Problem ten będzie zilustrowany
przykładami w dalszej części opisu.
Wpływ składu roztworu na rozpuszczalność elektrolitow.
Powodem, dla ktorego stosujemy iloczyn rozpuszczalności a nie po prostu stęŜenie roztworu
nasyconego jest przede wszystkim moŜliwość obliczania rozpuszczalności w roztworach soli
a nie tylko w czystej wodzie. W przypadku, gdy roztwor zawiera jon wspolny z jonem
wytrącanego elektrolitu rozpuszczalność ulega zmniejszeniu. Wynika to z definicji iloczynu
rozpuszczalności. Zwiększenie stęŜenia jednego z jonow musi spowodować zmniejszenie
stęŜenia drugiego z jonow - inaczej iloczyn rozpuszczalności nie byłby stały. Zjawisko to
nazywamy efektem wspolnego jonu. W praktyce doświadczalnej często zdarza się, Ŝe na
efekt wspolnego jonu nakłada się zjawisko tworzenia związkow kompleksowych, zwłaszcza
dla duŜych stęŜeń elektrolitow o takim samym anionie. Wowczas rozpuszczalność osadu
ponownie zaczyna wzrastać. Wrocimy jeszcze do tego zagadnienia przy omawianiu wpływu
kompleksowania na rozpuszczalność osadow.
JeŜeli roztwor, w ktorym rozpuszczamy osad, nie zawiera jonow wspolnych z trudno
rozpuszczalnym elektrolitem, to wpływ stęŜenia tego roztworu jest mniejszy i objawia się
zwykle zwiększeniem rozpuszczalności. Wpływ ten wynika ze zmiany siły jonowej roztworu,
co ma wpływ na wspołczynniki aktywności a tym samym na warunkową, stęŜeniową stałą
rownowagi (K = Ka ・ fA
-m ・ fB
-n). PoniewaŜ ze wzrostem siły jonowej te wspołczynniki ulegają
zwykle obniŜeniu, powoduje to wzrost stałej stęŜeniowej, czyli iloczynu rozpuszczalności.
Określamy to zjawisko jako efekt obcego jonu.
Efekt wspólnego jonu
Przykład
Obliczyć, ile razy rozpuszczalność SrSO4 jest mniejsza w 0,01 M roztworze K2SO4 niŜ w
czystej wodzie. Iloczyn rozpuszczalności siarczanu strontu (dla I=0) wynosi 3,44・10-7.
Rozpuszczalność w czystej wodzie wynosi:
IR(SrSO4) = [Sr2+][SO4
2-], [Sr2+] = [SO4
2-] = C0
8
czyli ( ) 0 4 C I SrSO R = 5,86・10-4 M.
W wyniku rozpuszczania SrSO4 w roztworze K2SO4 mamy dwa źrodła jonow siarczanowych:
roztwor K2SO4 i rozpuszczony osad.
JeŜeli napiszemy odpowiednie rownanie rozpuszczania osadu to bez trudu zauwaŜymy, Ŝe po
zajściu postępu reakcji x, stęŜenia [Sr2+] ≠ [SO4
2-]
SrSO4 (s) = Sr2+ + SO4
2-
start 0 0,01
r-ga x 0,01+x
Mamy więc IR(SrSO4) = x(0,01+x). Uzyskujemy więc rownanie kwadratowe do rozwiązania.
Tutaj jednak, poniewaŜ rozpuszczalność osadu jest niewielka, moŜna załoŜyć, Ŝe 0,01+x
≅0,01 i IR(SrSO4) = x・0,01 i uprościć obliczenia do zwykłego dzielenia dwoch liczb.
x = IR/0,01 = 3,44・10-5 M.
PoniewaŜ x=[Sr2+], jest to jednocześnie rozpuszczalność naszego osadu w roztworze K2SO4.
Tak więc rozpuszczalność SrSO4 w czystej wodzie jest C0/x = 17 razy większa niŜ w 0,01 M
roztworze K2SO4.
W dokładniejszych obliczeniach lepiej wziąć stałą termodynamiczną dla obliczenia
rozpuszczalności w wodzie, ale stałą warunkową (dla I=3c= 0,03) dla obliczania
rozpuszczalności w roztworze K2SO4. W tablicach mamy wartość dla I=0,0 oraz 0,05 i po
interpolacji otrzymujemy: pK(0,03) = pK(0) + 0,03/0,05*(pK(0,05)- pK(0)) = 6,048 stąd
K(0,03) = 10-6.048 = 8,945・10-7. Po jej zastosowaniu otrzymujemy x=8,945・10-5 M, czyli 6,55
krotne zmniejszenie rozpuszczalności. Jest to skutek nakładania się efektow wspolnego i
obcego jonu. Jak widać wpływ siły jonowej na wyniki jest znaczny.
Zjawisko zmniejszenia rozpuszczalności w roztworze soli zawierającej jon wspolny z osadem
jest wykorzystywane w chemii analitycznej przy przemywaniu osadow. Przykładowo w
przypadku ilościowego oznaczania strontu, aby uniknąć nadmiernego rozpuszczania, osad
SrSO4 zamiast wodą lepiej jest przemywać np. rozcieńczonym roztworem siarczanu amonu.
Przykład
Do 50 cm3 0,1M roztworu AgNO3 dodano 50 cm3 0,5 M roztworu Na2SO4. Obliczyć, ile
miligramow jonow Ag+ pozostanie w roztworze.
Iloczyn rozpuszczalności Ag2SO4 (dla I=0) wynosi 1,2・10-5.
Napiszmy rownanie reakcji powstawania Ag2SO4 i dokonajmy bilansu liczby moli przed
reakcją i po reakcji.
2 AgNO3 + Na2SO4 = Ag2SO4 + 2 NaNO3
start 5・10-3 25・10-3 0 0
r-ga 5・10-3 -2x 25・10-3 -x x 2x
Obliczmy maksymalny postęp reakcji, zuŜywający całość AgNO3 lub całość Na2SO4 wg
wzoru C= C0 + x:
dla AgNO3 : 0 = 5・10-3 - 2x, stąd xmax= 2,5・10-3
dla Na2SO4: 0 = 25・10-3 -x, xmax2= 25・10-3
Jak widać mamy nadmiar siarczanu sodu, gdyŜ dla tego reagenta maksymalny postęp reakcji
mogłby wynosić 10 razy więcej.
ZałoŜmy, Ŝe reakcja zaszła praktycznie do końca i [Ag+] ≅ 0. MoŜemy wowczas obliczyć
stęŜenie nadmiarowego siarczanu sodu biorąc x≅2,5・10-3 i uwzględniając n=n0 +x:
[SO4
2-] = n/V = (25・10-3 -2,5・10-3) mol/0,1 dm3 = 22,5・10-3/0,1 M = 0,225 M
StęŜenie pozostałego Ag+ obliczymy z iloczynu rozpuszczalności (nie moŜe być dokładnie
zero, bo iloczyn rozpuszczalności ma niezerową wartość)
IR= [Ag+]2[SO4
2-]
9
czyli [Ag+] =
[ ] 2
4
− SO
I R = 0,00730 M.
Masę jonow srebra obliczymy jak zwykle ze wzoru m= CVM
mAg = 0,008433・0,1・108= 0,0789 g, czyli 78,9 mg.
Podobnie jak poprzednio, zadanie to moŜna rozwiązać dokładniej, uwzględniając zaleŜność
stałej rozpuszczalności od siły jonowej, wrocimy do tego problemu za chwilę.
Efekt obcego jonu.
Nasz sposob obliczania rozpuszczalności osadow w roztworach innych soli (bez jonow
wspolnych z osadem) będzie polegał na obliczeniu siły jonowej roztworu, następnie
odczytaniu z tablic warunkowej stęŜeniowej, względnie ich interpolację. Otrzymujemy
wowczas stałą stęŜeniową, ktorą moŜna stosować dla danej siły jonowej i prowadzić
obliczenia tak jak poprzednio przy uŜyciu stałej termodynamicznej (dla I=0). Tabelaryzacja
zastępuje inną procedurę polegającą na obliczeniu wspołczynnikow aktywności oraz
obliczeniu warunkowej stęŜeniowej stałej rownowagi poprzez dołączenie wspołczynnikow
aktywności do stałej termodynamicznej.
Przykład - elektrolit 1-1
Obliczyć rozpuszczalność AgCl w wodzie i w 0,1 M roztworze K2SO4.
Iloczyn rozpuszczalności AgCl wynosi 1,77・10-10.
Rozpuszczalność w wodzie: C=[Ag+] = R I = 1,33・10-5.
Rozpuszczalność w roztworze K2SO4. [K+]= 2C, [SO4
2-] = C.
Siła jonowa roztworu I = . (Cizi
2) = . (2・C・12 + C・22 ) = . 6C = 3C = 0,3M
Z tablic mamy KSo(I=0,2)= 3,5・10-10 i KSo(I=0,5) = 4,54・10-10.
Z interpolacji uzyskujemy pKSo(I=0,3)= 9,418 czyli KSo= 10-9,418 =3,82・10-10.
KSo(I=0,3) = 3,82・10-10 stąd skorygowana rozpuszczalność wyniesie:
So(I=0,3) = 10 3,82 10⋅ − = 1,95・10-5 M.
Jak widać, roŜnica jest znaczna i wynosi około 47%.
Przykład - elektrolit 1- 2
Obliczyć rozpuszczalność CaF2 w wodzie i 0,05 M roztworze KNO3.
Termodynamiczny iloczyn rozpuszczalności CaF2 wynosi 3,45・10-11.
Rozpuszczalność w wodzie. [Ca2+]=C, [F-]= 2C,
IR(CaSO4) = [Ca2+][F-]2 = 4C3, stąd C = 3
4
R I
C= 3 11 3,45 10 / 4 ⋅ − = 2,05・10-4 M.
Rozpuszczalność w roztworze KNO3.
Siła jonowa I=1/2 (0,05・12 + 0,05・12) = 0,05.
Warunkowa stała rownowagi wymaga podzielenia stałej termodynamicznej przez trzecią
potęgę średniego molowego wspołczynnika aktywności, gdyŜ stęŜenie teŜ występuje w 3
potędze. KSo(I=0,05) = KSo(I=0) f-3. Wartość tę mamy juŜ policzoną i umieszczoną w tabeli.
10
Z tabeli dla I=0,05 odczytujemy wartość warunkowej stałej rownowagi: 1,11・10-10 i liczymy
stęŜenie CaF2 w 0,1M roztworze KNO3: So =3
10
4
1,11 10⋅ − = 3,03・10-4 M.
RoŜnica jest znaczna i wynosi 48%.
Przykład - rozpuszczalność Ag2SO4 ponownie
Wracamy do poprzedniego zadania z tą roŜnicą, Ŝe uwzględnimy wspołczynniki aktywności i
uŜyjemy warunkowej, stęŜeniowej stałej rownowagi.
Przypomnijmy treść:
Do 50 cm3 0,1M roztworu AgNO3 dodano 50 cm3 0,5 M roztworu Na2SO4. Obliczyć, ile
miligramow jonow Ag+ pozostanie w roztworze.
Iloczyn rozpuszczalności (termodynamiczny, dla I=0) Ag2SO4 wynosi 1,2・10-5.
Poprzednio obliczyliśmy, Ŝe po zajściu reakcji pozostaje 0,225M nieprzereagowanego
Na2SO4 a w wyniku reakcji jednocześnie z wytworzeniem osadu powstaje 2x= 5・10-3 mola
NaNO3, co daje stęŜenie CNaNO3=5・10-3/0,1 = 0,05 M.
Obliczamy siłę jonową wynikającą z obecności Na+, SO4
2-, oraz NO3
-.
I = . ((0,225*2+0,05)・12 + 0,225・(-2)2 + 0,05・(-1)2) = . (0,5+0,9+0.05) = 0,725M
NaleŜy więc uŜyć warunkową stałą rownowagi dla I=0,725.
Z braku lepszych danych zastosujemy wartość z tablic dla I=0,5. KSo(I=0,5) = 1,89・10-4
Rozpuszczalność [Ag+] =
[ ] 2
4
− SO
KSo = 0,029 M.
Przypomnijmy poprzedni wynik: 0,00730 M.
Obecny wynik jest około 3,97 raza większy niŜ poprzednio. Jeszcze ilość miligramow srebra:
mAg = CVM = 0,029・0,1・108 = 0,313 g czyli 313 mg (wobec 78,9 mg otrzymanych
poprzednio).
PowyŜszy przykład wyraźnie wskazuje na konieczność stosowania warunkowych stałych
stęŜeniowych w praktycznych obliczeniach. Obliczenia prowadzone bez ich uwzględnienia
mają bardzo ograniczone zastosowanie pokazując jedynie trendy zmienności poszczegolnych
rozpuszczalności.
NaleŜy sobie jednak zdawać sprawę, Ŝe nawet obliczenia prowadzone z uwzględnieniem
wpływu siły jonowej sposobami przedstawionym powyŜej nie są pozbawione błędu, gdyŜ dla
duŜych wartości I wspołczynniki aktywności są uzaleŜnione od składu chemicznego
elektrolitu a nie tylko od samej wartości siły jonowej (inne dla NaClO4, inne dla KNO3 itd.).
Wytrącanie z mieszaniny, strącanie frakcyjne.
W przypadku prowadzenia wytrącania z roztworow o bardziej złoŜonym składzie obliczenia
prowadzimy według podanych powyŜej schematow, traktując kaŜdą z rownowag jako
niezaleŜną od innych. Ze względow praktycznych istotne są obliczenia słuŜące
zaprojektowaniu ilościowego wytrącenia pewnego z jonow oraz przewidywanie
selektywności wytrącania pewnych składnikow z mieszaniny. Standardowo zakłada się, Ŝe
jeŜeli stęŜenie jonu w roztworze jest mniejsze niŜ 10-5 mol/dm3 to moŜna uznać Ŝe został on
wytrącony ilościowo.
Przykład
Roztwor zawiera jednocześnie 0,03 mol/dm3 NaI, 0,05 mol/dm3 NaBr i 0,08 mol/dm3 NaCl.
Do tego roztworu stopniowo dodawano stęŜonego roztworu azotanu srebra. Oblicz, ktora z
soli srebra (AgCl, AgBr czy AgI) wytrąci się jako pierwsza i określ zakresy stęŜeń jonow
Ag+, w ktorych będą się wytrącać poszczegolne sole.
11
Iloczyny rozpuszczalności (dla I=0,1):
IR(AgCl) = 3,0・10-10; IR(AgBr) = 9,07・10-13; IR(AgI) = 1,44・10-16.
PoniewaŜ wszystkie osady są tego samego typu, 1-1, do oceny rozpuszczalności moŜemy
wykorzystać iloczyny rozpuszczalności. PoniewaŜ najmniejszy iloczyn rozpuszczalności IR
posiada AgI, naleŜy przypuszczać, Ŝe to właśnie on zostanie najprędzej przekroczony i jako
pierwszy wytrąci się osad AgI. Obliczmy stęŜenie jonow srebra, dla ktorego to nastąpi.
Zakładamy, Ŝe stęŜenia anionow praktycznie nie zmniejszyły się poprzez rozcieńczenie.
a) najmniejsze stęŜenie jonow Ag+ konieczne do rozpoczęcia wytrącania AgI:
[Ag+] = IR(AgI)/[I-] = 1,44・10-16/0,003 = 4,80・10-14 M,
b) początek wytrącania AgBr
[Ag+] = IR(AgBr)/[Br-] = 9,07・10-13/0,005 = 1,8・10-10 M,
c) początek wytrącania AgCl
[Ag+] = IR(AgCl)/[Cl-] = 3,0・10-10/0,008 = 3,75・10-8 M,
Tak więc w miarę zwiększania stęŜenia jonow srebra mamy następujące obszary. Od zera do
stęŜenia 4,80・10-14 M występuje roztwor nienasycony. PowyŜej tego stęŜenia wytrąca się AgI.
Jodek srebra wytrąca się jako jedyny, aŜ do osiągnięcia stęŜenia 1,8・10-10 M, od ktorego to
momentu rownocześnie zacznie wytrącać się AgBr. Dla rozpoczęcia wtrącenia AgCl stęŜenie
Ag+ musi wzrosnąć do wartości 3,75・10-8 M.
MoŜna tu rownieŜ postawić inne zadanie praktyczne. Ile moli czystego AgI moŜemy
maksymalnie wytrącić z 0,5 dm3 tego roztworu? W tym celu obliczymy stęŜenie jonow
jodkowych pozostałych w roztworze w momencie uzyskania nasycenia względem AgBr.
Skorzystamy z iloczynu rozpuszczalności AgI:
[I-]nasAgBr = IR(AgI)/[Ag+]nasAgBr = 1,44・10-16/1,8・10-10 = 8,0・10-7 M
W postaci osadu wydzieliło się więc
n = (C1 - C2)V = (0,003 - 8,0・10-6) ・0,5 = 1,496・10-3 mola.
PoniewaŜ cały roztwor początkowo zawierał 1,5・10-3 mola, stanowi to 99,73% osadu AgI.
Tak więc, gdyby udało nam się przerwać dodawanie azotanu srebra w odpowiednim
momencie moŜemy po odsączeniu osadu AgI dalej wytrącać nieco tylko zanieczyszczony
AgBr itd. Tego typu postępowanie nazywamy strącaniem frakcjonowanym.
Bardziej poprawne obliczenia powinny uwzględniać wzrost siły jonowej w trakcie
wytrącania. W punkcie a) moŜemy zastosować stałą termodynamiczną, w punkcie b)
musieliśmy wytrącić prawie 0,03 mola/dm3 AgI, a więc w roztworze mamy 0,03M roztwor
NaNO3 (I=0,03) i powinniśmy stosować KSo(AgBr, I=0,03), z kolei w punkcie c) stęŜenie
NaNO3 wzrasta do 0,03+0,05 = 0,08M i taka teŜ jest w przybliŜeniu siła jonowa. NaleŜy więc
znowu zamiast termodynamicznego IR(AgCl) uŜyć KSo(AgCl, I=0,08). Zastosowanie stałych
warunkowych dla I=0,1 jest pewnym przybliŜeniem ale nie prowadzi do duŜych błędow.
Oczywiście jakościowo sytuacja nie ulegnie zmianie.
Wpływ pH na rozpuszczalność osadow elektrolitow
Zagadnienie zaleŜności stęŜenia roztworu nasyconego danego osadu w funkcji pH ma duŜe
znaczenie praktyczne. Klasyczna analiza jakościowa kationow, wykorzystuje często roŜnice
w rozpuszczalności osadow w wodzie oraz w roztworach kwasow: mocnych oraz słabych.
Pewne osady trudnorozpuszczalne w wodzie ulegają rozpuszczeniu (roztworzeniu) w
roztworze słabego kwasu octowego a inne wymagają zastosowania roztworow mocnych
12
kwasow. Ilościowe podstawy tego postępowania wyjaśnimy w dalszej części tego rozdziału
posługując się wyraŜeniami na iloczyn rozpuszczalności oraz na stałą kwasowości.
W sposob analogiczny do efektu wspolnego jonu wartość pH roztworu wywiera wpływ na
rozpuszczalność wodorotlenkow.
Przykład
Obliczyć pH konieczne do ilościowego (<10-5M) wytrącenia Ŝelaza w postaci Fe(OH)3 z
roztworu zawierającego 0,01M FeCl3.
Siła jonowa roztworu wynika z obecności FeCl3 i wynosi 6c, czyli 0,06.
Z interpolacji do I=0,06 mamy pKSo=37,51, czyli 3,09・10-38
[OH-] = 3
[ 3 ] Fe
KSo
[OH-] =3
5
38
10
3,09 10
−
⋅ − = 1,448・10-11
Dla siły jonowej 0,06 stęŜeniowy iloczyn jonowy wody pKSo = 13,832 i f(H+)=0,83;
[H+] = 10-13,832/1,448・10-11 = 1,016・10-3 M
pH = log{H+} =log (f・[H+])= log (0,83・1,016・10-3) = 3,07
Wynika stąd, Ŝe dla wytrącenia ilościowego Ŝelaza(III) z roztworu wystarcza, jeśli pH jest
wyŜsze od 3,07.
Zwiększoną rozpuszczalność soli słabych kwasow w mocniejszych kwasach wyjaśnia się
poprzez ubytek anionu z roztworu związany z protonowaniem anionu z wytworzeniem
słabego kwasu. PoniewaŜ wartość iloczynu rozpuszczalności musi pozostać stała - ubytek
stęŜenia (aktywności) anionu na skutek powstawania słabego kwasu musi być
zrekompensowany przejściem do roztworu większej ilości osadu aŜ do osiągnięcia
wymaganego iloczynu stęŜenia anionu i kationu.
Przykład
Obliczyć stęŜenie nasyconego roztworu AgCN w wodzie i w roztworze zawierającym mocny
kwas dający [H3O+]=0,1M.
KSo(AgCN, I=0,0) = 6,02・10-17; KSo(AgCN, I=0,1) = 1,00・10-16;
KK(HCN, I=0,1) = 3,79・10-10
a) rozpuszczalność w wodzie (pomijamy hydrolizę anionu w wodzie).
Sow = So K = 7,76・10-9 M.
b) rozpuszczalność w roztworze mocnego kwasu
Musimy uwzględnić rownowagę rozpuszczania osadu łącznie z rownowagą protonowania
cyjankow, czyli z innej strony patrząc, rownowagą dysocjacji słabego kwasu, HCN.
KSo = [Ag+][CN-]
So = [Ag+]
So = [CN-] + [HCN]
Biorąc pod uwagę rownanie rownowagi dysocjacji HCN otrzymujemy:
KK = [CN-][H3O+]/[HCN] => [HCN] = [CN-][H3O+]/KK
13
czyli So =
−
K K
H O
CN
[ ]
[ ] 1 3 =
K
K
K
K H O
CN
[ ]
[ ] 3
−
Otrzymane wyraŜenia na stęŜenia jonow podstawiamy do wzoru na iloczyn rozpuszczalności:
KSo = [Ag+][CN-]
KSo = [Ag+][CN-] =
[ ] 3
K H O
SoSoK
K
K
i dalej wyprowadzamy wzor na rozpuszczalność :
So =
K
So K
K
K (K [H O ]) 3
So =
10
16 10
3,79 10
1,00 10 (3,79 10 0,1)
−
− −
⋅
⋅ ⋅
So = 1,62・10-4 M.
Rozpuszczalność w roztworze mocnego kwasu jest więc So/Sow około 20900 razy większa
niŜ w wodzie.
Dodatkowo wpływa tu efekt zwiększenia rozpuszczalności związany ze wzrostem siły
jonowej i zmiany KSo, ktory uwzględniliśmy poprzez uŜycie dwoch roŜnych stałych dla (I=0 i
I=0,1).
Rachunki wyglądają nieco inaczej, gdy mamy do czynienia z trudnorozpuszczalną solą,
pochodną kwasu dwu- lub więcej protonowego. Wowczas naleŜy uwzględnić kolejne stopnie
dysocjacji, zwłaszcza Ŝe anion wchodzący w skład osadu jest zwykle dwu- lub trojkrotnie
naładowany. Stopień skomplikowania daje się w pewnych przypadkach zmniejszyć, stosując
odpowiednie załoŜenia na temat proporcji stęŜenia jonow hydroniowych do stałych
kwasowości.
Przykład
Obliczyć czy z roztworu CdSO4 o stęŜeniu 0,01M, po nasyceniu siarkowodorem do stęŜenia
CH2S=0,1M wytrąci się CdS, jeśli pH = 2.
KSo(CdS) = 7,95・10-27
H2S: K1 = 1,0・10-7; K2 = 1,2・10-13
Naszym celem jest policzenie iloczynu analogicznego do iloczynu rozpuszczalności dla
sytuacji zdefiniowanej w treści zadania.
KSo(CdS) = [Cd2+][S2-]
Obliczenie stęŜenia kationow jest banalne (zakładamy całkowitą dysocjację CdSO4):
[Cd2+] = CCdSO4 = 0,01 M
Dla obliczenia stęŜenia jonow siarczkowych w obecności mocnego kwasu musimy posłuŜyć
się bilansem siarkowodoru oraz stałymi kwasowości kwasu siarkowodorowego
CH2S = [H2S] + [HS-] + [S2-]
K1 = [HS-][H+]/[H2S], K2= [S2-][H+]/[HS-]
skąd mamy, po wstawieniu wyraŜeń na [H2S] i [HS-]:
CH2S = [HS-][H+]/K1 + [S2-][H+]/K2 + [S2-]
CH2S = [S2-][H+]2/(K1・K2) + [S2-][H+]/K2 + [S2-]
CH2S = [S2-]( [H+]2/(K1・K2) + [H+]/K2 + 1), po sprowadzeniu do wspolnego
mianownika
CH2S = [S2-] ([H+]2 + K1 [H+] + K1・K2 )/(K1・K2)
ostatecznie
14
[S2-] = (CH2S ・K1・K2)/ ([H+]2 + K1 [H+] + K1・K2 )
co, o ile [H+] >>K1 co ma miejsce dla pH<5 moŜna uprościć do
[S2-] = CH2S ・K1・K2/ [H+]2
Teraz moŜemy przystąpić do obliczenia stęŜenia jonow siarczkowych dla pH=2. PoniewaŜ
jest to mniej niŜ 5 zastosujemy wzor uproszczony.
[H+] = 10-pH = 10-2 M
[S2-] = CH2S ・K1・K2/ [H+]2 = 0,1・1,2・10-7・10-13/ (10-2)2 = 1,2・10-21/10-4 = 1,2・10-17 M
WyraŜenie na iloczyn jonowy [Cd2+][S2-] przyjmuje więc wartość
[Cd2+][S2-] = 0,01・1,2・10-17 = 1,2・10-19 co jest liczbą większą od iloczynu rozpuszczalności
KSo(CdS) = 7,95・10-27. Układ w celu dojścia do rownowagi musi wytworzyć pewną ilość
osadu, aby obniŜyć stęŜenia jonow Cd2+ i S2- i sprowadzić ich iloczyn do wartości KSo.
Tak więc osad CdS w tych warunkach wytrąci się.
Przykład
Roztwor, zawierający 0,05M Mn(NO3)2 nasycono gazowym siarkowodorem do uzyskania
stęŜenia całkowitego CH2S = 0,1 M (bez zmiany objętości całkowitej cieczy). Czy z takiego
roztworu wytrąci się MnS, jeŜeli pH wynosi 5? Ile wynosi graniczne pH dla rozpoczęcia
wytrącenia MnS z takiego roztworu?
KSo(MnS) = 1,0・10-8.
Tym razem uŜyjemy pełnego rownania kwadratowego w celu wyliczenia stęŜenia jonow
siarczkowych:
[S2-] = (CH2S ・K1・K2)/ ([H+]2 + K1 [H+] + K1・K2 )
[S2-] = 1,2・10-21/ ((10-5)2 + 10-7・10-5 + 1,2・10-20)
[S2-] = 1,2・10-21/1,01・10-10 = 1,188・10-11
Stąd [Mn2+][S2-] = 0,05・1,188・10-11 = 5,94・10-13 < KSo(MnS)
Tak więc z roztworu o pH=5 osad się nie wytrąci.
Wyznaczmy teraz graniczne pH. Graniczne stęŜenie jonow siarczkowych wyznaczymy z
iloczynu rozpuszczalności:
[S2-] = KSo(MnS)/[Mn2+]
[S2-] = 1,0・10-8 / 0,05 = 2,0・10-7 M
Aby osiągnąć to stęŜenie siarczkow dla CH2S=0,1M wymagane jest stęŜenie [H+] wynikające
z podanego powyŜej rownania na stęŜenie siarczkow, teraz [H+] jest szukaną zmienną.
[H+]2 + K1 [H+] + K1・K2 = CH2S ・K1・K2 / [S2-]
[H+]2 + 10-7・[H+] + 1,2・10-20 = 1,2・10-21/2,0・10-7 = 6,0・10-15
[H+]2 + 10-7・[H+] - 6,0・10-15 = 0
Otrzymane rownanie kwadratowe rozwiązujemy stosując zwykłą procedurę z deltą.
= b2 -4ac = (10-7)2 -4・(-6,0・10-15) = 10-14 + 2,4・10-14 = 3,4・10-14
[H+] = (-b +√)/2a = 4.219・10-8
pH = -log [H+] = 7,375 (pomijamy wspolczynnik aktywności jonu H+(aq))
Stwierdzamy, Ŝe aby z roztworu zawierającego 0,05 M Mn2+ oraz 0,1M H2S wytrącić MnS
naleŜy pH roztworu doprowadzić co najmniej do pH=7,375.
(W dokładniejszych obliczeniach naleŜy wziąć stałe dla siły jonowej określonej dla roztworu
Mn(NO3)2: I=3c =0,15. PoniewaŜ H2S jest praktycznie niezdysocjowany moŜna go pominąć
15
przy wyznaczaniu siły jonowej. Podobnie przeliczenie z pH na [H+(aq)] powinno uwzględnić
aktywność jonu wodorowego dla I=0.15).
Wzory podane dla kwasu siarkowodorowego są po odpowiednim podstawieniu słuszne
rownieŜ dla innych kwasow dwuprotonowych i ich anionow, np. szczawianow, węglanow,
siarczanow(IV), chromianow(VI) itd. Oczywiście, wowczas zakres pH w ktorym obowiązuje
wzor uproszczony naleŜy uzaleŜnić od aktualnej wartości stałej K1, tak aby relacja [H+] >>K1
była spełniona. ZałoŜmy, Ŝe będziemy stosować wzor uproszczony dla [H+]> 100K1.
Wpływ kompleksowania na rozpuszczalność osadow elektrolitow
Wpływ kompleksowania na rozpuszczalność osadow elektrolitow łatwo zrozumieć na
zasadzie analogicznej jak dla roztwarzania w kwasach. PoniewaŜ tworzenie jonu
kompleksowego zmniejsza stęŜenie jonu metalu, układ musi rekompensować ten ubytek
poprzez zwiększenie rozpuszczalności aŜ do momentu, w ktorym zostanie przywrocona
rownowagowa wartość iloczynu rozpuszczalności.
Podobnie jak poprzednio, aby uzyskać ilościowe wyniki, musimy w obliczeniach obok
bilansow oraz definicji iloczynu rozpuszczalności uwzględnić rownanie wynikające z
definicji stałej trwałości danego kompleksu.
W praktyce analizy jakościowej kationow oznacza to, Ŝe poprzez dodanie odpowiednio
selektywnego odczynnika kompleksującego dany kation, moŜemy zapobiec wytrąceniu
osadow soli tego kationu. Czynność tę czasami nazywa się maskowaniem jonu.
Przykład
Obliczyć rozpuszczalność AgBr w wodzie i porownać ją z rozpuszczalnością w 0,2M
roztworze amoniaku.
KSo(AgBr)= 5,0・10-13, (Ag(NH3)2
+) = 2,5・107,
So= [Ag+] + [Ag(NH3)2
+],
So= [Br-].
W wodzie oczywiście nie ma kompleksowania Ag+ amoniakiem i rozpuszczalność liczymy
poprzez pierwiastkowanie iloczynu rozpuszczalności
So= √KSo = 7,07・10-7 M.
Skorzystamy z definicji stałej trwałości i wyznaczmy wyraŜenie na stęŜenie kompleksu
=
2
3
3 2
[ ][ ]
[ ( ) ]
Ag NH
Ag NH
So= [Ag+] + [Ag+][NH3]2 = [Ag+](1+ [NH3]2)
Podstawiając [Ag+] i [Br-] do iloczynu rozpuszczalności otrzymujemy
KSo=
2
3 1 [NH ]
SoSo
So = (1 [ ] ) 2
3 K NH So
Ze wzoru wynika, Ŝe rozpuszczalność AgBr wzrasta ze wzrostem stęŜenia amoniaku oraz jest
tym większa im większa jest stała trwałości tworzonego kompleksu.
JeŜeli stała trwałości jest bardzo duŜa, to często w sumie moŜna pominąć jedynkę.
W naszym konkretnym przypadku mamy:
So = √(5,0・10-13(1 + 2,5・107・0,2・0,2) = √(5,0・10-13(1 + 1,0・106))
16
So = 7,07・10-4 M.
W 0,2 M roztworze amoniaku rozpuszczalność AgBr jest 1000 razy większa niŜ w wodzie.
Przykład
Ile moli amoniaku naleŜy dodać do 100 cm3 0,01 M roztworu AgNO3, aby po dodaniu 50 cm3
0,2 M roztworu NaCl nie wytrącił się osad AgCl? ZałoŜyć, Ŝe dodanie NH3 nie spowoduje
zmiany objętości.
Rozwiązanie.
JeŜeli osad AgCl nie ma się wytrącić to iloczyn [Ag+][Cl-] nie moŜe przekroczyć wartości
KSo(AgCl). ZałoŜmy, Ŝe te dwie wielkości są sobie rowne.
Musimy pamiętać o wzajemnym rozcieńczeniu roztworow, zakładamy brak kontrakcji
roztworow na skutek mieszania.
po rozcieńczeniu: [Cl-] = 0,2 M ・50 cm3 / 150 cm3 = 0,667 M
mamy więc krytyczne stęŜenie Ag+: [Ag+] = KSo(AgCl)/[Cl-]
[Ag+] = 1,6・10-10/0,667 = 2,4・10-10 M
Bilansowe stęŜenie srebra w tym roztworze wynosi (z uwzględnieniem rozcieńczenia)
CAg = 0,01 M ・100 cm3 / 150 cm3 = 0,00667 M
Ze względu na bardzo małe stęŜenie wolnych jonow Ag+ załoŜymy, Ŝe CAg jest rowne
stęŜeniu jonow kompleksowych Ag(NH3)2
+. PoniewaŜ osad AgCl nie ma być wytrącony, taki
bilans jest uzasadniony i CAg ≅ [Ag(NH3)2
+].
Ze wzoru na stałą trwałości kompleksu mamy:
=
2
3
3 2
[ ][ ]
[ ( ) ]
Ag NH
Ag NH
[NH3] =
[ ]
[ ( ) ] 3 2
Ag
Ag NH
= √(0,00667/(2,5・107・2,4・10-10)) =√(1,1111)
[NH3] = 1,054 M.
Na końcu naleŜy zauwaŜyć, Ŝe dodawany amoniak zuŜywany jest rownieŜ na wytworzenie
Ag(NH3)2
+, stąd mamy bilansowe stęŜenie
CNH3 = [NH3] + 2 [Ag(NH3)2
+] = 1,054 + 2・0,00667 = 1,067 M
Wspołczynnik dwa przed stęŜeniem soli kompleksowej wynika z faktu, Ŝe na wytworzenie 1
mola kompleksu potrzebne są 2 mole amoniaku.
Tak więc całkowita liczba moli amoniaku wyniesie:
n= CNH3 ・V= 1,067mol/dm3・0,150 dm3 = 0,1601 mola
Do obliczeń wzięliśmy objętość końcową, bo to w tym właśnie, końcowym roztworze
musimy zapewnić właściwe stęŜenie NH3.
Odpowiedź: aby zapobiec wytrąceniu AgCl do roztworu AgNO3 naleŜy dodać 0,16 mola
NH3.
7.6. Rozwiązywanie zagadnień prowadzących do rownań wyŜszego rzędu.
WyraŜenia występujące w zagadnieniach związanych ze stanami rownowagi dosyć często
prowadzą do rownań będących wielomianami rzędu wyŜszego niŜ dwa. O ile dla wielomianu
stopnia trzeciego istnieją wzory (chociaŜ są bardzo skomplikowane i mało godne polecenia)
umoŜliwiające napisanie gotowego rozwiązania o tyle dla wielomianow wyŜszego rzędu tego
typu wzory analityczne nie istnieją. Problem obliczania stęŜeń rownowagowych jest jednak
dosyć szczegolny, gdyŜ wiadomo, Ŝe rozwiązanie na pewno istnieje, a poza tym musi spełniać
17
warunek narzucany przez stechiometrię. A więc stęŜenia muszą być liczbami dodatnimi a
poza tym nie moŜna przekraczać maksymalnych ilości bilansowo dostępnych w układzie.
Problem jest więc lepiej określony niŜ w matematyce dla dowolnych wielomianow.
JeŜeli w układzie występuje tylko jedna reakcja chemiczna, to ułoŜenie odpowiedniego
rownania nie nastręcza trudności. Najprościej do rownania na stałą rownowagi wpisać
stęŜenia początkowe skorygowane o przebieg reakcji poprzez postęp reakcji C=C0 + vi・x.
Znalezienie miejsca zerowego otrzymanego wielomianu umoŜliwia obliczenie wszystkich
stęŜeń w stanie rownowagi. Jest wiele metod numerycznego rozwiązywania tego typu
zagadnień (metoda bisekcji, regula falsi, metoda stycznych Newtona itp.).
Przykład:
Oblicz stęŜenia rownowagowe wszystkich substancji, obecnych w roztworze zawierającym
0,01 mol/dm3 Pb(NO3)2 i 0,5mol/dm3 CH3COOK. W roztworze mamy obecne w wyniku
dysocjacji powyŜszych soli jony Pb2+ oraz CH3COO-, ktore biorą udział w reakcji tworzenia
kompleksu: Pb2+ + 4 CH3COO- = Pb(CH3COO)4
2- .
Stała trwałości tego kompleksu wynosi: ([Pb(CH3COO)4]2-) = 25,7.
Napiszmy wyraŜenie na stałą rownowagi:
=
4
3
2
2
3 4
[ ][ ]
[ ( ) ]
−
−
Pb CH COO
Pb CH COO
ZałoŜmy, Ŝe powstało x moli produktu. Z definicji postępu reakcji mamy:
[Pb(CH3COO)4
2-] = 0 +x,
[Pb2+] = 0.01 -x,
[CH3COO-] = 0,50 -4x.
Wartości te podstawmy do wzoru na stałą rownowagi. Otrzymamy następujący wielomian:
(0.01-x)(0,50-4x)4 ・ 25,7 = 0,0 + x.
Utworzmy z niego funkcję F(x), ktora w przypadku podstawienia rownowagowej wartości x
będzie dawała zero. F(x) = x - (0.01-x)(0,50-4x)4 ・ 25,7
Teraz musimy tylko znaleźć miejsce zerowe tego wielomianu. Zastosujmy metodę stycznych
Newtona, ktora w przypadku znalezienia się blisko rozwiązania daje bardzo dobrą zbieŜność.
Odpowiedni wzor iteracyjny wygląda następująco:
xi+1 = xi - F(xi)/F'(xi)
Obliczmy pochodną (stosując wzor na pochodną iloczynu):
F'(x) = 1 - 25,7・((-1)・(0,50-x)4 + (0.01-x)・4・(0.5-x)3)
Oczywiście, jeŜeli komuś jest wygodniej, moŜna wykonać mnoŜenia zawarte w nawiasach i
sprowadzić wielomian do postaci F(X) = a0 + a1 x + a2 x2 + a3 x3 + a4 x4 + ... , ktory jest
łatwiej roŜniczkować.
Teraz pozostaje tylko znalezienie startowego przybliŜenia x1. Właściwie prawie zawsze
moŜna rozpocząć z x=0, albo, gdy jest to miejsce zerowe pochodnej, bierzemy np. połowę
wielkości maksymalnej x. W naszym przypadku z bilansu ołowiu widać, Ŝe x<=0,01.
Prześledźmy zbieŜność procesu dla a) x1=0 i b) dla x1=0.005.
i xi F(xi) F'(xi) xi+1
a) x1=0.0
1 0,00 -0,0160625 2,47775 0,006482696
2 0,006482696 0,001916968 2,481091429 0,005710065
3 0,005710065 -5,23469・10-6 2,480864515 0,005712175
4 0,005712175 9,05316・10-8 2,480865197 0,005712139
5 0,005712139 -3,21814・10-10 2,480865185 0,005712139
18
b) x1 = 0.005
1 0,005 -0,001821315 2,48061563 0,005734219
2 0,005734219 5,57002・10-5 2,4808723 0,005711767
3 0,005711767 -9,39147・10-7 2,480865065 0,005712146
4 0,005712146 1,73441・10-8 2,480865188 0,005712139
5 0,005712139 -3,21814・10-10 2,480865185 0,005712139
Jak widać, niezaleŜnie od punktu startowego, po pięciu krokach, uzyskujemy rozwiązanie dla
x=0,0057124.
Teraz juŜ moŜemy łatwo obliczyć stęŜenia rownowagowe:
[Pb(CH3COO)4
2-] = 0 +x = 0,00571 M
[Pb2+] = 0.01 -x = 0,00429 M
[CH3COO-] = 0,50 -4x = 0,47715 M.
W tym przykładzie stała kompleksowania jest niewielka, co uwidacznia się w stopniu
skompleksowania jonow ołowiu wynoszącym 57,1% - pozostałe 42,9% Pb2+ nie tworzy
kompleksu.
W obliczeniach praktycznych moŜna posłuŜyć się programowalnym kalkulatorem,
programem Microsoft Excel lub, w miarę moŜliwości, samemu napisać jakiś prosty program
np. w języku JavaScript lub Visual Basic.
50
Wyszukiwarka
Podobne podstrony:
zwiazki kompleksowe 2
Sprawozdanie 6 związki kompleksowe
Cw2 Zwiazki kompleksowe
otrzymywanie i właściwości związków kompleksowych
7 Związki kompleksowe
Sprawozdanie z ChOiA zwiazki kompleksowe ćw 3
Sprawozdanie NR 5 związki kompleksowe
Zwiazki kompleksowe
wykład 10 związki kompleksowe
Związki kompleksowe (kompleksy, związki koordynacyjne
Analiza związków kompleksowych ćwiczenie
Budowa atomu i związki kompleksowe
związki kompleksowe
Związki kompleksowe kobaltu
Związki kompleksowe, AGH różne, chemia wykłady
Mechanizmy reakcji związków kompleksowych
zwiazki kompleksowe 3 id 593625 Nieznany
Związki kompleksowe
więcej podobnych podstron