T E C H N I K A P O M I A R Ó W

I Pojęcia podstawowe:

Narzędzia pomiarowe - są to środki techniczne przeznaczone do wykonywania pomiarów a należą do nich:

• wzorce

• przyrządy pomiarowe

• przetworniki pomiarowe

• układy pomiarowe

• systemy pomiarowe

• Wzorce:

Wzorce - są to narzędzia pomiarowe odtwarzające jednostki miary lub ich wielokrotności

Parametry wzorców:

• 
  nominalna miara wzorca np. 1,0000 kg, 10,000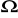
  

• niedokładność wykonania miary wzorca ( błąd wzorca) np. 0,05 %

np. 100 kg
1 kg; 1kg =
błąd bezwzględny wzorca

1%; 1% =
błąd względny wzorca

• warunki w których miara niedokładności wzorca jest zachowana

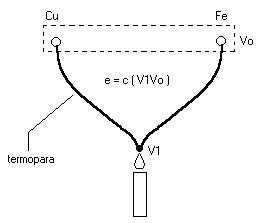
1. wzorce napięcia:

• elektrochemiczny - ogniwo Westona. Parametry ogniwa Westona:

• wartość znamionowa napicia 1,018540 - 1,018730 [V]

• prąd maksymalny I_max < 1
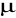
  A

• wrażliwość na wstrząsy

elektroniczne, w większości wzorców elektronicznych stosujemy diody Zenera, które to elementy decydują o jakości tego wzorca
) Rezystory wzorcowe jednomiarowe - rezystory te odtwarzają jedną wartość rezystancji:

• zakres rezystancji 0,002
  - 1 k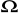
  stosowane 2 pary zacisków tzw. Zaciski napięciowe i prądowe

Zaciski prądowe umożliwiają polepszenie dokładności pomiaru gdyż dzięki nim wyeliminowany jest wpływ rezystancji styku związany z istnieniem przewodów doprowadzających prąd w zakresie rezyst. > 1 k
stosowana jedna para zacisków

Charakterystyka rezystancji jednomiarowych klasy dokładności: 0,0005; 0,001; 0,002; 0,005; 0,01; o,o2; 0,05; 0,1; 0,2

Symbol diody Zenera:

Jeżeli przez diodę Zenera wymusimy przepływ prądu ( a nastąpi to tylko wtedy gdy siła elektromotoryczna e źródła zasilania przekroczy wartość tzw. napięcia Zenera ) to spadek napięcia na diodzie będzie miał wartość prawie niezależną od wartości prądu płynącego przez tą diodę. Inaczej mówiąc jeżeli będziemy zwiększać siłę kompensujących się strumieni magnetycznych ( strumieni o przeciwnych kierunkach i równych wartościach)

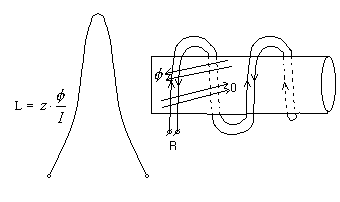
Nawijanie bifilarne:

elektromotoryczną e źródło zasilania, to będzie się zwiększał prąd płynący przez diodę ale napięcie na tej diodzie praktycznie pozostanie bez zmian a ściślej biorąc będzie się bardzo niewiele zwiększać. Dotyczy to zakresu prądu od 5 [mA] - kilkadziesiąt [mA]

Dioda Zenera ma za zadanie zapewnić wstępną stabilizację napięcia zasilającego obwód z diodą D₂ . Jako diody służące do wytwarzania napięć wzorcowych stosowane są diody Zenera o napięciach od 5,6 V - 6 V gdyż w tym zakresie napięcie Zenera obserwuje się bardzo małe, nawet zerowe występowanie

współczynników temperaturowych napięć Zenera.

2. Wzorce rezystancji - są to odpowiednio skonstruowane rezystory wykonane z drutu i taśm rezystancyjnych. Materiały oporowe i ich właściwości:

• materiały:

np: konstantan, manganin (84% Cu, 12% Mn, 4% Ni)

Najszersze zastosowanie znalazł manganin. Wzorce wykonane z manganinu , po odpowiednim sztucznym starzeniu zmieniają rezystancję zaledwie o kilka dziesięciotysięcznych procenta w ciągu roku.

R_Cu20^o = 100

R_Cu21^o = 100,4

R_Cu1900^o = 99,6

zmiana 01⁰C

R = 0,4

R_Cu40^o = 108

• Wymagania dotyczące właściwości:

* mały wsółczynnik temp. rezystancji np:

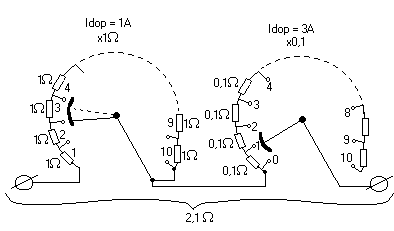
* duża rezystancja właściwa ( in. Oporność właściwa, rezystywność)

* małą siła termoelektryczna względem miedzi

) Rezystory wzorcowe jednomiarowe - rezystory te odtwarzają jedną wartość rezystancji:

• zakres rezystancji 0,002
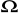
  - 1 k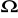
  stosowane 2 pary zacisków tzw. Zaciski napięciowe i prądowe

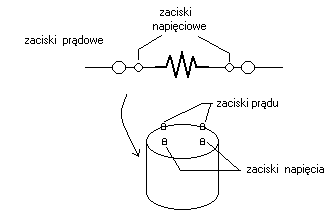
Zaciski prądowe umożliwiają polepszenie dokładności pomiaru gdyż dzięki nim wyeliminowany jest wpływ rezystancji styku związany z istnieniem przewodów doprowadzających prąd w zakresie rezyst. > 1 k
stosowana jedna para zacisków

Charakterystyka rezystancji jednomiarowych klasy dokładności: 0,0005; 0,001; 0,002; 0,005; 0,01; o,o2; 0,05; 0,1; 0,2

Klasa dokładności rezystora jest to błąd procentowy wykonania wartości rezystancji tego rezystora.

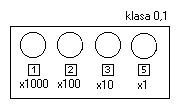
Rezystory wzorcowe wielomianowe - są to rezystory umożliwiające uzyskanie różnej wartości rezyst. Wzorcowych nazywa je się często rezystorami dekadowymi.

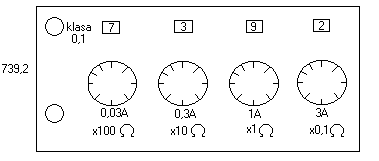
Rezystor dekadowy:

Zalecenia użytkowe:

Wartość rezystancji opornika dekadowego jest pokazywana w okienkach umieszczonych nad pokrętłami poszczególnych dekad, każde pokrętło ma 9 niekiedy 10 pozycji a więc umożliwia wybranie dowolnej liczby z danej dekady.

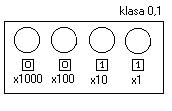
Wartość rezystancji wypadkowej jest sumą ustawionych poszczególnych wartości. Każda z dekad ma dopuszczalny prąd opisany na płycie czołowej rezystora dekadowego a więc o max. prądzie płynącym przez rezystor dekadowy decyduje najsłabsze ogniwo. Jeżeli początkowe dekady ( o najwyższych wartościach ) mają zerowe wartości to o prądzie dopuszczalnym decyduje i z dekad w której okienku

pojawi się wartość inna niż 0, w naszym przypadku z wartości

R = 1,2

Imax = 1 A

Klasa rezystora dekadowego - informuje nas o procentowym błędzie wartości rezystancji ustawionej w okienkach rezystora dekadowego, np:

1,2

0,1%

37,5

0,1%

37,5

0,1%

• ogólna charakterystyka

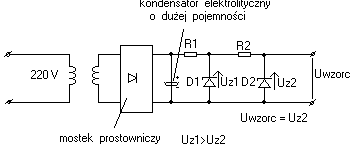
BĘDZIE NA EGZAMINIE (schemat wewnętrzny)

• schemat wewnętrzny układu rezystora dekadowego

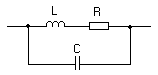
Ze schematu wewnętrznego możemy możemy wnioskować, że rezystory każdej dekady są nawinięte drutem o innej grubości, przy czym zasada jest taka, że w miarę wzrostu mnożnika dekady stosowany drut ma coraz mniejszą średnicę, a wiemy że im mniejsza średnica drutu tym mniejszy jest prąd dopuszczalny który może płynąć przez ten drut. W miarę wzrostu dekady mamy mniejszy prąd dopuszczalny. Teoretycznie biorąc byłoby możliwe nawinięcie rezystorów wszystkich dekad identyczną średnicą drutu, ale w takim przypadku rezystory dekad o dużych mnożnikach osiągnęłyby duże gabaryty. W przypadku prądu stałego spiralne nawinięcie rezystora nie ma żadnego znaczenia dla wartości oporu jaki on stawia prądowi stałemu gdyż indukcyjność L, która powstaje na skutek tego spiralnego nawinięcia nie ma żadnego wpływu na wartość prądu w stanie ustalonym. W przypadku prądu zmiennego zwłaszcza przy częstotliwościach odpowiednio dużych mamy schemat zastępczy opornika w którym znajduje się szeregowe połączenie rezystancji R i reaktancji X_L. W rezultacie źródło napięcia widzi opór zwany impedancją obliczoną z zależności z =
, której wartość może przekraczać wartość rezystancji R.

Pełny schemat zastępczy rezystora zawiera również pojemność montażową.

Schemat zastępczy rezystora:

Aby uniknąć problemu wpływu indukcyjności rezystora wzorcowego stosuje się specjalny sposób tzw. Nawijanie bifilarne, dzięki któremu teoretycznie możemy indukcyjność zredukować do zerowej wartości a w praktyce do bliskiej 0. Istota działania uzwojenia bifilarnego polega na wytworzeniu w uzwojeniu rezystora dwóch kompensujących się strumieni magnetycznych ( strumieni o przeciwnych kierunkach i równych wartościach)Nawijanie bifilarne:

Konstruktorzy zgodnie z wymaganiami PN powinni deklarować że w zakresie częstotliwości prądu sinusoidalnego od 0 - 1 kHz rezystor dekadowy można traktować jako czystą rezystancję a więc opór który stawiał prądowi zmiennemu ma wartość dokładnie taką jaka wynika z pokrętła na tym rezystorze.

2 Przyrządy pomiarowe:

Są to narzędzia pomiarowe przeznaczone do wykonywania pomiarów.

Schemat przyrządu pomiarowego to:

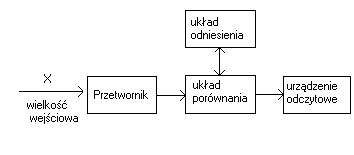
3. Przetwornik pomiarowy:

Ten podzespół który przetwarza wielkość mierzoną x na łatwiej mierzalną wielkość y.

• Układ pomiarowy:

Zbiory przyrządów i przetworników pomiarowych, umożliwiają pomiar mierzonej wielkości: Y = f ( x₁, x₂, x₃ )

Wielkość mierzona jest określona na podstawie innych wielkości i obliczona na podstawie konkretnej jednoznacznej zależności funkcyjnej.

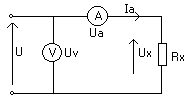
Przykład:

Rx =

Uv > Ux

4. Systemy pomiarowe:

Zbiory funkcjonalne przyrządów i przetworników pomiarowych objęte wspólnym sterowaniem umożliwiającym pobieranie i przetwarzanie informacji.

II Metody pomiarowe:

Określa sposób porównania wielkości mierzonej z wzorcem tej wielkości. Mamy dwa podstawowe kryteria podziału: Podział ze względu na sposób uzyskiwania wyniku pomiaru:

a) metoda bezpośrednia - wielkość mierzona odczytana przy użyciu odczytu przyrządów pomiarowych. Nie potrzeba dodatkowych obliczeń poza niezbędnym minimum

b) metoda pośrednia - uczestniczy w nie więcej urządzeń pomiarowych. Wartość wielkości mierzonej zwykle obliczona jest w zależności funkcyjnej

Y = f ( x₁, x₂, x₃, ... )

Ustalonej teoretycznie lub doświadczalnie, w której to zależności występują wielkości mierzone bezpośrednio.

2. podział ze względu na sposób pomiaru i sposób zastosowania wzorca:

BĘDZIE NA EGZAMINIE (metody pomiarowe, np. przedstaw przykłąd metody ... nie muszą być definicje)

1. metoda odchyłowa - pomiar miernikiem elektromechanicznym, którego wskazanie zależy od wielkości mierzonej

b) metoda zerowa - aby otrzymać wynik pomiaru układ pomiarowy jest tak skonstruowany aby pewną wielkość doprowadzić do zerowej wielkości. Stosunek mierzonej i znanej (wzorzec) wielkości tej samej wartości doprowadza się do określonej zależności matematycznej której wynik często równa się jedności.

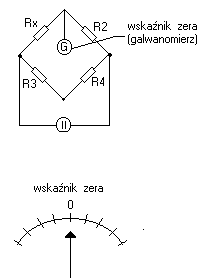
Przykładem tej metody jest mostek Wheatsto ne'a

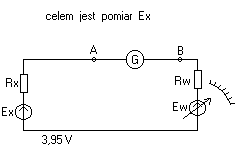
c) metoda kompensaacyjna - jest tam również wskaźnik zera, który wskazuje zerowe napięcie.

Przykład

Ew - napięcie zasilacza

Ex - szukane napięcie

Ex = Ew

Gdy wskaźnik galwan. = D czyli V_A = V_B

W stanie kompensacji dokonujemy pomiaru siły elektromotorycznej Ex gdyż w obwodzie nie płynie prąd a więc niema spadku na rezystancji wewnętrznej tego źródła Rx. Podobnie rezystancja szeregowa Rw wywołana np. obecnością długiego przewodu łączącego regulowane źródło Ew z pozostałą częścią układu również niema znaczenia, gdyż nie występuje na tej rezystancji Rw spadek napięcia.

d) metoda podstawieniowa - wielkość mierzoną x porównuje się z wielkością wzorcową w ten sposób, że skutki wywołane przez wielkość wzorcową podstawioną za wielkość mierzoną są identyczne.

Przykład:

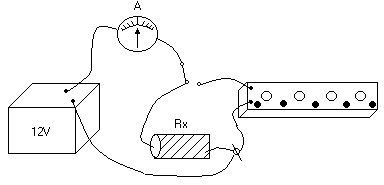
Rezystancję Rx można zmierzyć jak na rys. powyżej podstawiając w jej miejsce rezystor dekadowy i regulując tym rezystorem dekadowym tak aby wskazanie miliamperomierza było identyczne jak w sytuacji gdy w obwodzie umieszczony był rezystor Rx.

e) inne metody.

III Podstawy rachunku błędu:

Wynik pomiaru powinien być podany z błędem pomiaru, wynik pomiaru stanowi istotną wartość informacyjną ale musi on być podawany łącznie z informację o
błędzie, którym ten wynik jest obarczony.

1. Liczbowa miara błędów:

1. Błąd bezwzględny, poprawka, błąd bezwzględny graniczny

1. błąd bezwzględny:

- błąd bezwzględny

W₀ - wartość odczytana (wskazana)

W_r - wartość rzeczywista

Błąd bezwzględny:

Różnica między wartością odczytaną na podstawie pomiaru a wartością rzeczywistą.

Wartość rzeczywistą zastępujemy wartością poprawną czyli tak bliską wartości rzeczywistej, że z punktu widzenia pragmatyki pomiarów różnica pomiędzy nimi może być pominięta.

Właściwości błędu bezwzględnego:

• ma konkretną wartość i znak

• nie nadaje się do porównywania dokładności narzędzi pomiarowych o różnych zakresach pomiarowych,

np:

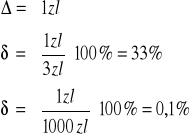
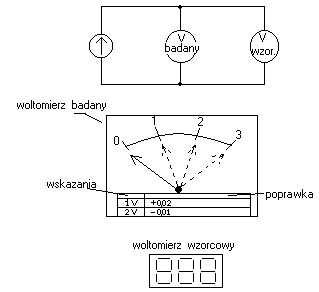
2. poprawka - błąd bezwzględny ze znakiem minus:

Poprawka pozwala określić wartosć rzeczywistą wskazania przyrządu pomiarowego przez ssumowanie wartości otrzymanej zw wskazania tego przyrządu i wartością poprawki uzyskanej z tabeli dołączonej do dokumentacji przyrządu.

Np:

V badane	V wzorc.
[V]	[V]	[V]	[V]
1,00	1,02	-0,02	+0,02
2,00	1,99	+0,01	-0,01
3,00	3,05	-0,05	+0,05

3. Błąd bezwzględny graniczny:

Błąd graniczny wyznacza wartości graniczne
które może się zmienić. Błąd graniczny pozwala określić przedział wartości w którym znajduje się wartość rzeczywasta wielkości mierzonej. W odróżnieniu od błędu bezwzględnego błąd graniczny, nie pozwala na poprawienie dokładności pomiaru, charakteryzuje się:

• graniczne wartości wzięte ze znakiem
  

• wyrażony w jednostkach wielkości mierzonych

Obszar zakreskowany to obszar w którym znajduje się wartość rzeczywista.

Przykład zapisu z błędem granicznym:

107,0 [V] + 2,5 [V]

107,0 [V] - 2,5 [V]

Pojęcie błędu granicznego jest znacznie częściej stosowane przez pomiarowców, gdyż korzystając z przyrządu pomiarowego można na podstawie dokumentacji technicznej lub na podstawie oznaczeń na mierniku określić wartość bezwzględnego błędu granicznego.

Błąd bezwzględny graniczny oznaczony takim symbolem jak błąd bezwzględny czyli

delta bez indeksu, jedynie na podstawie oznaczenia
interpretujemy to że mamy do czynienia z błędem granicznym,

np:

1. Błąd względny, błąd względny graniczny:

1. Błąd względny:

W₀ - wartość otrzymana

W_r - wartość rzeczywista

Ponieważ w większości przypadków wartość rzeczywistej nie jesteśmy wstanie określić i wstawiamy w to miejsce wartość poprawną.

W niektórych przypadkach w mianowniku jest wartość otrzymana

Właściwości:

• wyrażony jest w jednostkach niemianowanych lub w procentach w niektórych przypadkach, zwłaszcza literatura angielskojęzycznych używany jest mnożnik ppm 10^-6

np:
=0,001 = 1000 * 10^-6 = 1000 ppm

• ma konkretny znak ( + lub - ) i wartość

• pozwala na porównanie dokładności mierzonych wielkości na różnych zakresach pomiarowych.

ZADANIA NA EGZAMIN:

Zadanie:

Porównać dokładność pomiarów odległości l₁ i l₂:

l₁=100m ,
l₁ = 0,5m,

l₂ = 5000m,
l₂=-5m,

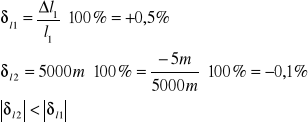
2. błąd względny graniczny:

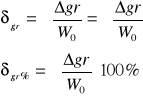
Często w zapisie technicznym rezygnujemy z indeksu gr i tylko po zapisie znaku (
) rozpoznajemy błąd graniczny.

Przykładem błędu granicznego jest klasa rezystorów dekadowych podawana jako liczba na obudowie dekady rezystora. Przez ten wskaźnik klasy należy rozumieć procentowy

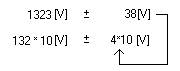
błąd graniczny dowolnie ustawionej wartości tej dekady:

W₀=1235

W₀=11

Wynik pomiaru z błędem bezwzględnym granicznym możemy zapisać w sposób następujący:

np.

123 [V]
2 [V]

W przypadku błędu względnego jest zapisem nieformalnym.

Poprawny zapis:

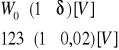
ZADANIE NA EGZAMIN:

Zad.

Stwierdzono że błąd bezwzględny
błąd względny po dokonaniu obliczeń
.

Ile wynosiła wartość mierzona W₀.

= 0,02

1. Zasady zaokrąglania liczbowego wyniku pomiaru i błędu:

Wynik pomiaru powinnien być zapisany w taki sposób aby najmniej znacząca cyfra informowała o rzędzie wartości błędu bezwzględnego.

Zasady zaokrąglania:

I zaokrąglanie błędu - zawsze staramy się zaokrąglać liczbę do do 1 cyfry znaczącej chyba, że zaokrąglenie jest zbyt duże, a konkretnie przekracza 20% surowego błędu. W takim przypadku należy pozostawić (zaokrąglić ) 2 cyfry znaczące błędu. Wynik błędu zawsze będziemy zaokrąglać w górę.

II Zaokrąglanie wyniku pomiaru - wynik pomiaru zaokrąglamy do tylu liczb znaczących, których rząd odpowiada rzędom zapisu zaokrąglonego błędu.

NA EGZAMINIE (poniższy przykład):

Przykład 1:

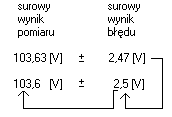
Sprawdzenie:

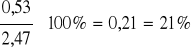
Wynik zaokrąglamy zgodnie z zasadami matematyki w górę albo w dół.

Przykład 2:

Sprawdzenie:

Przykład 3:

2. Klasyfikacja błędów:

1. Błędy systematyczne:

Są to błędy których wartość i znak są znane, tzw. systematyczne właściwe, oraz błędy, których znane są wartości graniczne tzw. systematyczne niewłaściwe.

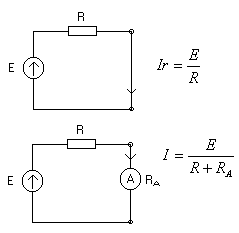
Błędy systematyczne właściwe - mogą się ujawnić między innymi na skutek efektu poboru mocy z układu pomiarowego. Inaczej mówiąc spowodowane są skończonymi rezystancjami woltomierza - powinna być nieskończ. a nie jest, amperomierza - powinna mieć zero i ma a także inne przyrządy watomierza, licznika energii. Błąd taki często też nazywamy błędem systematycznym metody pomiarowej.

Zad.

Poniżej przedstawimy przykład powstawania takiego błędu metody wywołanego skończoną rezystancją amperomierza.

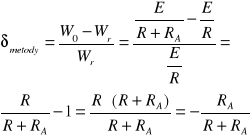
1. błędy systematyczne niewłaściwe - są to błędy graniczne , które można określić na podstawie wskaźnika klasy narzędzia pomiarowego bądź informacji zawartej w dokumentacji technicznej.

2.2. Błędy przypadkowe - zmieniają się w sposób losowy co do wartości jak i znaku przy wykonywaniu serii pomiarów w warunkach niezmienionych. Istnienie tych błędów stwierdza się otrzymując wyniki pomiarów różniących się od siebie ostatnimi cyframi znaczącymi.

Błąd przypadkowy i-tego wymiaru obliczamy ze wzoru:

Xi - wynik i-tego pomiaru

n - liczba wszystkich wyników.

Wśród błędów przypadkowych należy wyeliminować te błędy, które bardzo odbiegają od pozostałych.

3. Opracowanie wyników pomiaru:

1. Pomiar jednorazowy bezpośredni - pomiar, który wprost odczytujemy z przyrządu pomiarowego. Jednorazowy tzn. Pomiar wykonany tylko 1 raz:

Mierniki wskazówkowe - błąd pomiaru określa się za pomocą wskaźnika klasy , zwany też klasą miernika
- wyrażona w procentach. Błąd to nie jest klasa. Klasa miernika jest podawana zawsze na skali miernika:

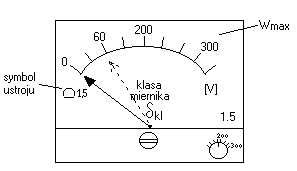
Klasa miernika pozwala wyliczyć błąd pomiaru dla danego wskazania z następujących zależności.

Błąd bezwzględny graniczny:

Niezależny od wartości wskazanej

Błąd względny graniczny:

W₀ - wartość otrzymana z pomiaru

Błąd względny procentowy gr.

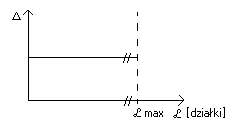
Przebieg błędu w funkcji wskazania:

Błąd bezwzględny graniczny wskazań miernika nie zależy od wartości wskazania, jest stały ( dla każdej wartości identyczny )

Błąd względny graniczny jest tym mniejszy im większy jest mianownik, zależy od wartości wskazanej. Najmniejszą wartość błąd ten osiąga wtedy gdy wskazanie W₀ jest równy zakresowi miernika Wmax.

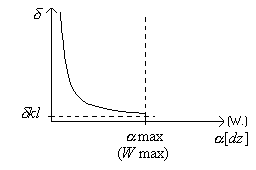
WNIOSKI:

Zawsze dobieramy taki zakres miernika aby wskazanie było jak najwyższe wtedy będzie stosunkowo mały błąd względny.

NA EGZAMINIE (zadanie)

Zad. 1.

Błąd bezwzględny i względny wskazań woltomierza o wskaźniku klasy 1,5 zakres 300 [V], a wartości wskazań są następujące.

W₁ : 45 [V]

W₂ : 90 [V]

W₃ : 300 [V]

W₁ : 45 [V]:

W₂ : 90 [V]:

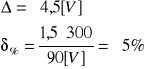
W₃ : 300 [V]

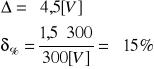
Zad. 2.

Żądamy aby błąd względny pomiaru wskazanie miernika miał wartość co najwyżej = 3%. Dysponujemy miernikami o zakresach 300 [V]

Wartość zmierzona wynosi 200 [V]. Ile powinna wynosić klasa miernika aby zapewnić żądaną dokładność pomiaru.

Mierniki cyfrowe

W przypadku mierników cyfrowych błąd oblicza się na podstawie zależności matematycznej - wzoru podawanego w instrukcji. Nie ma tej informacji na płycie czołowej, trzeba sięgnąć do instrukcji. W instrukcji podawany jest błąd bezwzględny, którego ogólna postać wynosi

np.

wartości + 5 najmniej

odczytane znaczące

(reading) cyfry wskazania (rozdzielczość miernika)

Przykład 1.

Watomierz cyfrowy o zakresie 199,9V

rozdzielczość : 0,1V
1 dg

błąd bezwzględny

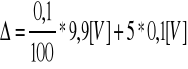
błąd względny graniczny

Niektórzy producenci umieszczają informację o błędzie bezwzględnym miernika cyfrowego w nieco inne formie zapisu matematycznego

WNIOSKI:

W odróżnieniu od miernika wskazówkowego błąd bezwzględny
nie ma wartości stałej i zależy od wartości wskazowej W
. Podobnie jak w miernikach wskazówkowych, starajmy się aby wyświetlonych zostało jak najwięcej cyfr znaczących, gdyż błąd względny maleje w miarę wzrostu wskazania.

Sposób obliczania błędu najczęściej bezwzgl. Podawany jest w instrukcji miernika (jest to niewygodne) przy czym zależności bywają odmienne od różnych producentów.

3.2

Pomiar jednorazowy pośredni( na podstawie wzoru)

Y=f(

Y- wynik pomiaru

(
-wartości mierzone bezpośrednio

np. pomiar rezystancji metodą techniczną

R

Y=

Błędy wielkości mierzonej bezpośrednio

przenoszą się na błąd całkowity wyniku pomiaru

(

Metody do obliczania błędu względnego wyniku pomiaru

*Metoda różniczki zupełnej (stosowana najczęściej).Metoda ta jest słuszna przy założeniach:

-błędy wielkości mierzonych bezpośrednio
mają stosunkowo małą wartość

-funkcja jest ciągła Y=f(

Różniczka zupełna jest to w zasadzie rozwinięcie funkcji y=f(
w szereg Taylora

a) błąd bezwzględny obliczamy metodą różniczki zupełnej

Wzór podstawiony wyżej jest przydatny, gdy są dane znaki błędów

. Pzwala to na przeprowadzenie wnioskowania na temat wzajemnej koncepcji. Jeżeli znamy błędy

to należy stosować wzór na znaki bezwzględne.

b) błąd względny

Jeżeli mamy do czynienia z błędami granicznymi, to powinniśmy wziąć pod uwagę gorszy przypadek

Przykład 2.

Na egzamin

Y=

x
x

x
x

Wykazaliśmy, że względny błąd jest sumą błędów

Warto zapamiętać zależności na błąd względny wyniku pomiaru
dla kilku podstawowych funkcji matematycznych

*iloczyn

Y =x

+

*iloraz lub iloczyn i iloraz

Y=

+

*suma arytmetyczna

Y =x

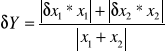
*różnica

Y =x

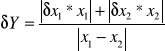
zad.1

Na egzamin

Moc pobieraną przez rezystor określona za pomocą pomiaru metodą pośrednią dokonując pomiaru błędu płynącego przez rezystor i mierząc omomierzem wartość tej rezystancji

R=10

Natężenie prądu zmierzono miernikiem wskazówkowym

I=5A

Należy obliczyć max błąd pomiaru mocy

oraz moc

Obliczamy metodą różniczki zupełnej

P=I

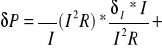
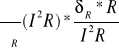
Wniosek:

SP=2*1,5%+2%=5%

P=I
=25*10=250W

P=250(1

3.3

Pomiar bezpośredni wielokrotny

3.3.1

Wprowadzenie

Wyniki pomiar…ów obarczone błędami przypadkowymi można traktować jako zmienne losowe podlegające prawom statystyki matem. i rachunku prawdopod.

Jeżeli wykonamy n pomiarów obarczonych błędami przypadkowymi i otrzymamy zbiór wyników

x

i=1

to wyniki te będą się losowo różnić od siebie. Można je zaprezentować w postaci histogramu

n

n

n- liczba pomiarów o tych samych wynikach lub wynikach z uwzględnieniem pewnej tolerancji

n
-całkowita liczba pomiarów

x-wartość mierzonej wielkości

Jeżeli zwiększymy liczbę pomiarów to uzyskamy krzywą ciągłą f(x) którą będziemy nazywać funkcją gęstości prawdopodobieństwa

Dla cel…ów metrologii najczęściej wykorzystujemy dwa rodzaje rozkładów wyników:

*Rozkład normalny Gaussa-Laplace'a

f(x)

x

*Rozkład jednostajny

Rozkład , który dotyczy błędów wnoszonych przez aparaturę pomiarową

F(x)

Dla mierników wskazówkowych

3.3.2

Opracowanie wyników pomiarów

W praktyce mamy do czynienia z ograniczoną ilością pomiarów n tej samej wielkości. W jaki sposób określić wykonanie pomiaru, jeżeli każdy z pomiarów ma różniące się wartości i w jaki sposób określić ten błąd, którym ten wynik jest opatrzony, a który to błąd będzie nas informował w jakim przedziale liczbowym znajduje się wartość rzeczywista

* wynik pomiaru:

wartość średnia

Wartość średnia to nie jest jednak wartość rzeczywista

• Wyznaczenie niepewności całkowitej U
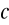
  . Niepewność całkowita jest w pewnym stopniu odpowiednikiem błędu granicznego, w przeszłości nazywano ją błąd graniczny wartości średniej.

• W odróżnieniu od pojęcia błędu granicznego, które gwarantuje w 100%, że przedział wartości będzie wynosić(w których znajduje się wartość rzeczywista) wynosi
  

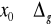
w tym przedziale będzie wartość rzeczywista

W przypadku niepewności całkowitej nie ma 100% pewności ,że w przedziale
mieści się wartość rzeczywista

Prawdop. będzie zawsze sprowadzone do pewnej wartości, na którą ma wpływ pomiarowiec dokonujący wyliczeń

Zał

Wszystkie poniższe rozważania są dokonywane przy założeniu, że błąd aparatury wynikający z klasy przyrządu jest pomijalnie mały, a więc przyczyną rozrzutu wyników są wyłącznie przyczyny postronne

*Obliczamy tzw. Niepewność standardową typu U
jest tzw. odchylenie standardowe wartości średniej

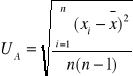
*Obliczamy niepewność całkowitą U

1. Gdy n>30 pomiarów

U

Wartość tego współczynnika wzięta jest z analizy rozkładu normalnego Gaussa

k
dla prawdop. 95%

k
dla prawdop. 99%

Przyjęcie przez mierzącego wartości k
jest praktycznie dowolne. W odpowiednich tablicach można znaleźć szczegółowe informacje w których żądanemu prawdop. jest przypisana ściśle określona k
. Np. jeżeli satysfakcjonuje nas prawdopodob. 95% to przyjmujemy k
=2. W rezultacie bardzo powiększyłby się nam przedział wartości, w których znajduje się wartość rzeczywista

2. Gdy n<30

Współczynnik k wyznacza się w inny sposób, na podstawie tablic rozkładu Studenta

Poniżej przedstawiono pewien fragment tablic Studenta

Prawdo podo ństwo n-1	90%	95%	99%
1	6,31	12,71	63,66
2	2,92	4,30	9,92
3	2,35	3,18	5,84
4	2,13	2,78	4,60
5	2,02	2,57	4,03

n-1=5-1=4

U

k
- wyznaczany jest z tablic Studenta na podstawie zał. Przez siebie prawdop. i na podstawie liczby n wykonanych pomiarów. Jeżeli wykonamy 5 pomiarów n=5 i przyjmujemy prawdop. 95%, to wartość k
=4,60

Przykład 3.

Wykonano 5 pomiarów napięcia

U

U

U

U

U

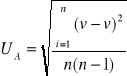
U
0,05099[V]

U

Szukamy k
dla prawdopod. 99%

U
=4,60*0,05099V=0,234554V

IV MIERNIKI ANALOGOWE ( ze wskazówkami)

1. Wprowadzenie- nazewnictwo, definicje, podstawowe pojęcia

Mierniki analogowe są to mierniki, których wskazania są funkcją ciągła wartości wielkości mierzonej. W zasadzie można przyjąć, że pod pojęciem mierniki analogowe kryją się mierniki elektromechaniczne. Pojęcia dotyczące mierników elektromechanicznych.

• ustrój miernika- przetwornik elektromech. który przetwarza bezpośrednio wielkość mierzoną na wielkość mechaniczną a konkretnie na kąt odchylenia wskazówki
  

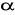
• organ ruchomy- część ruchoma ustroju

• funkcja przetwarzania miernika elektromech.-jest to zależność matem., która opisuje zależność kąta odchylenia od wielkości mierzonej x

=f(x)

Gdy
=c*x - funkcja liniowa, to przedziałka jest wtedy liniowa(równomierna)> Jest to najbardziej zalecana właściwość ustroju

Jeżeli zależność będzie nieliniowa, to i podziałka będzie nieliniowa

Rodzaje mierników elektromechanicznych

miernik magnetoelektryczny

mierniki elektromagnetyczne

miernik elektrodynamiczny

miernik ferrodynamiczny

2.Mierniki elektromechaniczne

momenty mechaniczne, równanie przetwarzania

Budowa wagi sprężynowej

k

x=

x= c* m podziałka liniowa

2.1.Momenty mechaniczne

a)Moment napędowy- jest to wielkość bezpośrednio związana z wielkością mierzoną np. prąd i wielkościami charakteryzującymi ustrój miernika np. indukcja magnetyczna magnesu, ilość zwojów cewki.

Wykres dotyczy ustroju magnetoelektrycznego

Pożądane jest aby M
nie zależał od kąta odchylenia wskazówki ale od wielkości mierzonej

zależność liniowa

W przypadku miernika elektromagnetycznego moment napędowy zależy od kąta odchylenia
wskazówki i jest to wada, która powoduje że podziałka będzie nierównomierna. W przypadku miernika elektromagnetycznego mamy dodatkowo jeszcze jedną wadę, moment napędowy nie jest liniową funkcja prądu. W mierniku elektromagnet. Stosowane są specjalne zabiegi konstrukcyjne, które minimalizują efekty nieliniowości

Wykres momentu napędowego dla miernika elektromagnetycznego

b)moment zwrotny- źródłem momentu zwrotnego w większości miernika jest sprężynka zwinięta spiralnie. Podstawową właściwością jest to, że jej moment zwrotny jest

k
-stała zwracania sprężyny

-kąt odchylenia ustroju ( kąt odchylenia wskazówki)

c)równanie przetwarzania

parametry konstrukcyjne miernika

Równanie przetwarzania wyznaczamy na podstawie przyrównania funkcji opisującej moment napędowy z funkcją opisującą moment zwrotny, gdyż położenie ustalone wskazówki będzie miało miejsce dla równości obu momentów

M

Charakter przedziałki możemy łatwo przewidzieć dokonując analizy metodą graficzną

podziałka liniowa

dla

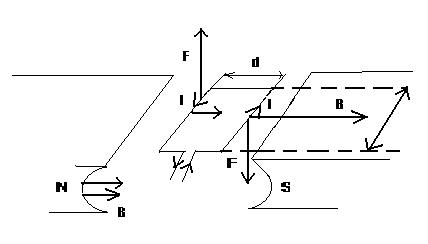
M

podziałka nieliniowa

2.2 Czułość i stała miernika

czułość- stosunek odpowiedzi do bodźca

S=

Y=

S=

x- wielkość mierzona

-odchylenie wskazówki

Pojęcie czułości jest nieco rzadziej używane, częściej stosujemy pojęcie stała miernika, oznaczana C

C=

Stała miernika jest wykorzystywana szczególnie wtedy, gdy wskazania są kłopotliwe do szybkiego odczytu ze względu na skomplikowane powiązania ilości działek z wartością liczbową wyniku U

Obliczam wartość stałej miernika C

C=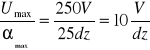

U

U

U

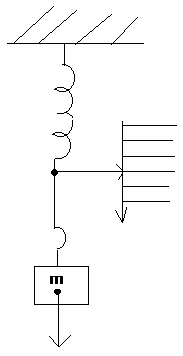
3. Miernik magnetoelektryczny

1. Budowa i zasada działania

1. Budowa

Źródłem momentu napędowego jest wzajemne oddziaływanie pola magnetycznego magnesu stałego i pola magnetycznego uzwojenia cewki nawiniętej na karkaz o prostokątnym kształcie

Moment zwrotny wytwarza spiralna sprężynka, która jednocześnie wykorzystana jest do połączenia elektr. zacisku wejściowego miernika z cewką

Organem ruchomym jest cewka, do której przymocowana jest wskazówka

Częściami nieruchomymi jest magnes, nabiegunnik, rdzeń ferromagnetyczny umieszczony wewnątrz cewki

Zadaniem rdzenia jest skierować wektory indukcji magnet. promieniście w kierunku środka

Moment tłumiący wytwarzany jest dzięki zastosowaniu aluminiowej ramki, na którą nawinięta jest cewka

W trakcie ustalania wskazań w bramce tej indukują się prądy, których pole magnetyczne przeciwdziała ruchom ramki, dzięki czemu ilość oscylacji wokół położenia równowagi jest niewielka

Na egzamin

2. Zasada działania

Wektor indukcji jest od N do S

W wyniku przepływu prądu i oddziaływania pola magnetycznego o indukcji B na oba boki ramki o dł. l działa para sił oznaczonych literą f, których to para sił wywoła obrót.

Wartość każdej z tych obliczamy według prawa Biot'a - Savart'a

F=B*I*l*z

M

M

Ponieważ mamy do czynienia z dwoma momentami napęd. Wywołującymi obrót w tym samym kierunku

2M

2*B*I*l*z*

stała

Równanie przetwarzania

Odchylenie wskazówki
jest proporcjonalne do prądu płynącego przez ustrój elektromagnetyczny

Jeżeli przez ustrój elektromagnetyczny płynie prąd zmienny okresowy o dostatecznie szybkich zmianach, czyli okres tego przebiegu ma małą wartość, to wskazanie wskazówki miernika będzie proporcjonalne do wartości średniej

I

W przypadku , gdy przebieg jest przebiegiem sinusoidalnym, to

I=Im sin

I

Na egzamin

Sposób graficzny wyznaczania wartości średniej

S
[cm

[cm

I

S
=S

1. Zastosowanie ustroju magnetoelektrycznego do budowy amperomierza

3.2.1 Amperomierz

1. Amperomierz bezpośredni- ustrój magnetoelektryczny reaguje na prąd, wskazanie jest
   zależne od prądu) a więc ustrój jest sam w sobie amperomierzem. Będziemy go nazywać amperomierzem bezpośrednim.

Zmieniając parametry konstrukcyjne(np. ilość zwojów, stałą zwracania sprężyny, indukcję magnet.) Można budować amperomierze o prądowych zakresach bardzo małe o zakresach na poziomie μA, ale także znacznie większe tzn. rzędu mA. W praktyce amperomierze bezpośrednie mają zakresy <25A. Budowa na wyższe wartości prądów oznaczałaby konieczność stosowania grubszego drutu i w konsekwencji zwiększenie ciężaru i gabarytu

2. amperomierz z poszerzonym zakresem

Dzięki zastosowaniu bocznika, czyli rezystora równolegle dołączonego do cewki uzyskujemy efekt poszerzenia zakresu. Efekt ten uzyskuje się przez to, że prąd I rozdziela się na dwie składowe, z których zwykle znacznie większa płynie bocznikiem a pozostała przez ustrój

I

I
prąd znamionowy ustroju wywołujący max odchylenie wskazówki

I-prąd nowego(powiększonego) zakresu

//:

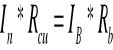
krotność zmiany zakresu amperomierza

R

R

Układ do poszerzania zakresu przedstawiony na powyższym rysunku nie ma znaczenia praktycznego, gdyż jego wadą jest podatność na wpływy temp. Zmiana temp. wpływa na wartość rezystancji cewki
wykonanej z miedzi np. wzrost temp. wywoła wzrost rezystancji cewki i w konsekwencji wskazanie miernika zmniejszy się, przy niezmienny prądzie wejściowym

Rezystancja bocznika jest const

W celu zminimalizowania wpływu temp. zastosow. Zmodyfikowany układ, nazywany kompensacją temperaturową

nie zależy od temp.

---