Miareczkowanie pH-metryczne kwasu octowego przed podziałem

Przybliżone stężenie CH3COOH [mol/dm^3]	Objętość CH3COOH Vk użyta do miareczkowania [cm^3]	Całkowita objętość NaOH zużyta do miareczkowania CH3COOH [cm^3]
0,3	5	16,5
0,4	5	22,0
0,5	4	22,5
0,6	4	26,6
0,7	3	23,4
0,8	3	27,2
0,9	2	25,8
1,0	2	22,3

Miareczkowanie pH-metryczne kwasu octowego po podziale

Przybliżone stężenie CH3COOH [mol/dm^3]	Objętość CH3COOH Vk użyta do miareczkowania [cm^3]	Całkowita objętość NaOH zużyta do miareczkowania CH3COOH [cm^3]
0,3	5	14,1
0,4	5	19,0
0,5	4	22,2
0,6	4	24,4
0,7	3	20,7
0,8	3	21,5
0,9	2	18,1
1,0	2	18,9

Celem ćwiczenia było wyznaczenie współczynnika podziału kwasu octowego między wodę i chloroform oraz parametru asocjacji kwasu octowego w chloroformie.

Współczynnika podziału Nernsta K_c jest wielkością charakterystyczną dla danego układu dwóch cieczy i składnika rozdzielającego się między te ciecze.

Współczynnika podziału Nernsta K_c w stałej temperaturze przyjmuję wartość stałą, jest to stosunek stężeń substancji rozpuszczonej w obu fazach ciekłych. W fazie wodnej substancja rozpuszczona ulega dysocjacji, w organicznej asocjacji. Wartość współczynnika podziału wskazuję, w jakim stopniu dana substancja dzieli się (rozpuszcza się w cieczach) między dwie ciecze. Różnice rozpuszczalności wykorzystuję się w ekstrakcji do rozdziału mieszanin wieloskładnikowych.

Opracowanie wyników:

1. Stężenie kwasu octowego przed podziałem C_i i po podziale
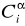
   w warstwie wodnej:

C_i =(C_z*V_z )/V_k

=(C_z*V_z )/V_k

V_k- objętość roztworu kwasu octowego pobrana do miareczkowania

C_z - stężenie zasady sodowej 0,1 mol/dm³

V_z- objętość roztworu zasady sodowej zużyta do miareczkowania

2. Stężenie kwasu octowego w warstwie chloroformowej
   :

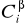
=C_i-

3. Stopień dysocjacji kwasu octowego
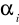
   w warstwie wodnej dla poszczególnych stężeń:

=0,003565-0,002812

4. Wykres zależności liniowej

lg[
(1-
)]=f (lg
)wyprowadzony ze zlogarytmowanej postaci równania

lg[
(1-
)]=lgK_c +1/n lg

• metodą najmniejszych kwadratów otrzymałam równanie y=0,1879x-0,0205, a więc

lg K_c=-0,0205, czyli K_c=0,94

1/n=0,1879, czyli n=5,32

• metodą graficzną otrzymałam

y₁=-0,14, y₂=-0,255, x₁=-0,7,x₂=-1,3

1/n= y₂ - y₁ / x₂ - x₁

1/n=0,19, n=5,26

lg K_c=-0,0351, K_c=0,92

Tabela wyników:

Ci [mol/dm^3]	[mol/dm^3]	[mol/dm^3]		1-	(1- ) [mol/dm^3]	lg[ (1- )]	lg
0,33	0,28	0,05	0,0071	0,9929	0,28	-0,55	-1,32
0,44	0,38	0,06	0,0063	0,9937	0,38	-0,42	-1,22
0,56	0,56	0,01	0,0052	0,9948	0,55	-0,26	-2,12
0,66	0,61	0,06	0,0050	0,9950	0,61	-0,22	-1,26
0,78	0,69	0,09	0,0046	0,9954	0,69	-0,16	-1,05
0,91	0,72	0,19	0,0045	0,9955	0,71	-0,15	-0,72
1,29	0,91	0,39	0,0038	0,9962	0,90	-0,05	-0,41
1,12	0,95	0,17	0,0037	0,9963	0,94	-0,03	-0,77

Stałe równania Nernsta	1/n	Kc	n
Metoda graficzna Metoda najmniejszych kwadratów	0,19 0,17	0,92 0,94	5,26 5,87

Wnioski:

Znajomość współczynników podziału substancji pomiędzy nie mieszające się fazy ciekłe ma ogromne znaczenie w ekstrakcji. W badanym przypadku rozdziału kwasu octowego pomiędzy fazą wodną a chloroformową, współczynnik podziału jest bliski jedności. Efektywne usunięcie kwasu octowego z roztworu wodnego do fazy chloroformowej wymagałoby kilkakrotnej ekstrakcji za pomocą kolejnych porcji czystego chloroformu.

---