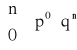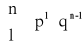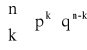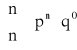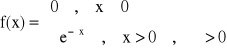RACHUNEK PRAWDOPODOBIEŃSTWA
Definicja przestrzeni probabilistycznej:
Przestrzenią probabilistyczną nazywamy trójkę (Ω, Σ, P), gdzie:
Σ - przestrzeń zdarzeń elementarnych
Ω - zbiór zdarzeń losowych
P - funkcja prawdopodobieństwa, P: Σ → <0,1>
Zdarzenie elementarne (Ω) - określa najprostszy wynik doświadczenia; każde zdarzenie elementarne wyklucza inne zdarzenie elementarne.
Przykład: - rzucamy sześcienną kostką do gry:
Ω = {e1, e2, e3, e4, e5, e6}, ei - wypadło i oczek
- rzucamy monetą:
Ω = {O, R}
Przestrzeń zdarzeń elementarnych (Σ) - rodzina podzbiorów przestrzeni Ω spełniającej warunki:
zbiór pusty Ø

Σjeśli A

Σ, to jego dopełnienie Ω - A
Σjeśli Ai

Σ, i=1,2,…, to suma
Elementy Σ nazywamy zdarzeniami losowymi. Zbiór Ø nazywamy zdarzeniem niemożliwym. Zbiór Ω - A = A' nazywamy zdarzeniem przeciwnym do A.
Twierdzenie:
Jeśli:
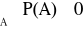
Ai

Σ, i
N oraz Ai
Aj = Ø, dla i ≠ jP(Ω) = 1
to:
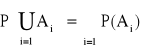
WNIOSEK:
P(Ø) = 0
UWAGA!!!
Zapis: Ai ![]()
Aj = Ø oznacza, że zdarzenia wykluczają się!!!
Definicja zmiennej losowej:
Zmienną losową nazywamy każdą funkcję X: Ω→R, spełniającą warunek, że dla każdej liczby rzeczywistej a, zbiór:
{w![]()
Ω: X(w) < a}
jest zdarzeniem, tzn. ![]()
Σ, a![]()
R.
Definicja dystrybuanty:
Dystrybuantą zmiennej losowej X nazywamy funkcję F, określoną wzorem:
F(x) = P(X<x) = P{w: X(w) < x}
Własności dystrybuanty:
dziedzina: R
zbiór wartości: <0,1>
jest funkcją niemalejącą,
jest lewostronnie ciągła na R
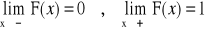
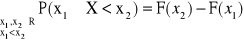
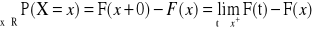
Rozróżniamy dwa typy zmiennych losowych:
ciągłe
dyskretne
Definicja zmiennej losowej ciągłej:
Zmienną losową X nazywamy zmienną losową ciągłą, jeśli istnieje taka nieujemna funkcja f, że dla każdej liczby rzeczywistej x dystrybuanta zmiennej jest określona wzorem:
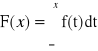
, f > 0
f - funkcja gęstości zmiennej losowej X.
Twierdzenie:
Jeśli gęstość f jest funkcją ciągłą w punkcie x0, to dystrybuanta F jest różniczkowalna w tym punkcie oraz zachodzi równość:
F'(x0) = f(x0)
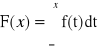
Przykład: Dla jakiego C![]()
R, funkcja f jest gęstością zmiennej losowej? Obliczyć dystrybuantę.
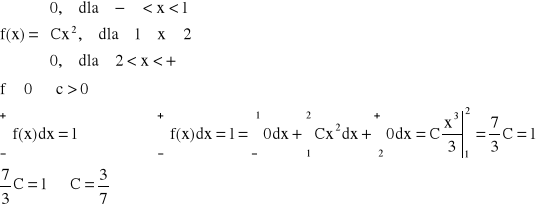
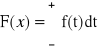
x < 1,
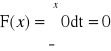
1 < x < 2,
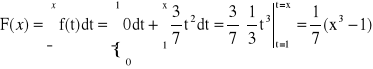
x > 2,
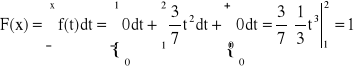
Dystrybuanta:
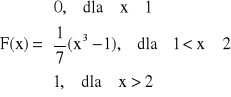
Twierdzenie:
Dystrybuanta zmiennej losowej ciągłej jest ciągła.
ROZKŁADY CIĄGŁE:
ROZKŁAD WYKŁADNICZY
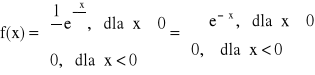
x > 0, α > 0
![]()
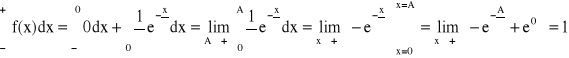
![]()
Dystrybuanta:
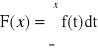
x < 0: 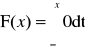
x > 0: 
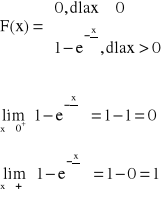
ROZKŁAD JEDNOSTAJNY
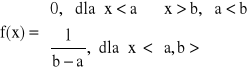
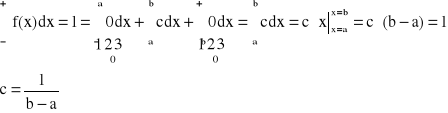
lub z pola prostokąta:
![]()
Dystrybuanta:
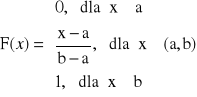
bo:
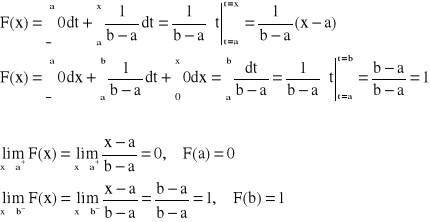
![]()
- funkcja liniowa
ROZKŁAD NORMALNY (GAUSSA) z parametrami m i b: N(m,σ)
Gęstość:
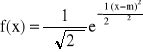
-∞ < x < +∞, m - dowolne, 0 < σ < +∞
Właściwości krzywej Gaussa:
symetryczna względem prostej x = m
ma maksimum dla x = m, f(m) =
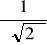
ma dwa punkty przegięcia: m - σ, m + σ
N(0,1) - rozkład normalny standaryzowany: 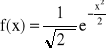
Twierdzenie:
Jeśli zmienna losowa X ma rozkład normalny N(m,σ), to zmienna losowa ![]()
ma rozkł. N(0,1).
Dystrybuanta: 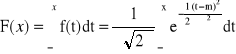
Dla N(0,1): 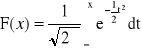
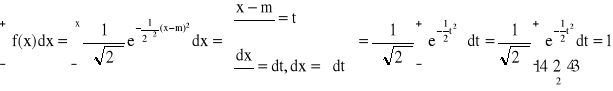
Rozkłady ciągłe:
gęstość: f(x) > 0,
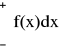
=1dystrybuanta: F(x) =
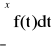
; funkcja ciągła F'(x0) = f(x0)wykres F jest ciągły
P{x1 < X < x2} =
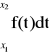
= F(x2) - F(x1)
ROZKŁADY DYSKRETNE
Definicja dyskretnej zmiennej losowej:
Zmienną losową X nazywamy dyskretną (skokową) jeśli przyjmujemy skończony lub przeliczalny zbiór wartości.
Elementów przeliczalnych jest tyle samo, co liczb naturalnych!!!
Skończona ilość wartości zmiennych losowych:
X |
x1 |
x2 |
… |
xn |
P(X=xi) |
p1 |
p2 |
… |
pn |
Nieskończona ilość wartości zmiennych losowych:
X |
x1 |
x2 |
… |
xn |
… |
P(X=xi) |
p1 |
p2 |
… |
pn |
… |
Definicja rozkładu prawdopodobieństwa:
Rozkładem prawdopodobieństwa (funkcją prawdopodobieństwa) zmiennej losowej dyskretnej X określonej na przestrzeni Ω nazywamy funkcję P przyporządkowującą wartościom P(X = xi) = pi, przy czym spełniony jest warunek: Σpi = 1.
![]()
pi > 0
WYKRES
HISTOGRAM
ROZKŁAD DWUPUNKTOWY
p > 0, q > 0
p + q = 1
X |
x1 |
x2 |
P(X=xi) |
p |
q |
Dystrybuanta:
F(x) = P(X < x)
x < x1
F(x) = 0
x1 < x < x2
F(x) = P
x > x2
F(x) = p +q = 1 ![]()
ROZKŁAD RÓWNOMIERNY
X |
x1 |
x2 |
… |
xn |
P(X=xi) |
p1 |
p2 |
… |
pn |
p + p + … + p = 1
n · p = 1 ![]()
Dystrybuanta:
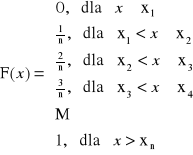
ROZKŁAD BERNOULLIEGO (dwumianowy) z parametrami n i p (0 < p < 1)
Definicja rozkłady Bernoulliego:
Mówimy, że zmienna losowa ma rozkład Bernoulliego z parametrami parametrami parametrami p (0 < p < 1) jeśli zmienna losowa X przyjmuje wartości k = 0,1,…,n z prawdopodobieństwem określonym wzorem:
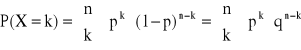
, gdzie q = 1 - p
k=0,1,…,n, n![]()
N
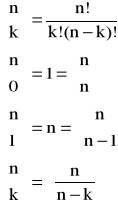
X |
0 |
1 |
… |
k |
… |
n |
P(X=k) |
|
|
… |
|
… |
|
P(X=k) > 0
Warunek unormowania:
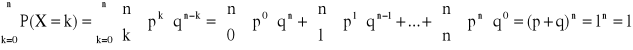
Przykład: n=4, p=![]()
Wykres prawdopodobieństw:
Dystrybuanta:
ROZKŁAD POISSONA
Definicja rozkładu Poissona:
Mówimy, że zmienna losowa X ma rozkład Poissona z parametrem λ (λ>0), jeśli zmienna losowa X przyjmuje wartości k = 0,1,2,… z prawdopodobieństwem określonym wzorem:
![]()
X |
0 |
1 |
2 |
… |
k |
… |
P(X=k) |
|
|
|
… |
|
… |
P(X=k) > 0
![]()
Twierdzenie Poissona (zastosowanie):
Jeśli zmienna losowa Xn ma rozkład Bernoulliego i jeśli dla n=1,2,… spełniony jest warunek: λ=n · p (λ>0), to:
![]()
W/w twierdzenie stosujemy dla dużych n i wtedy rozkład Bernoulliego można zastąpić rozkładem Poissona.
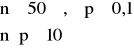
„dość” dokładnie
Dowód:
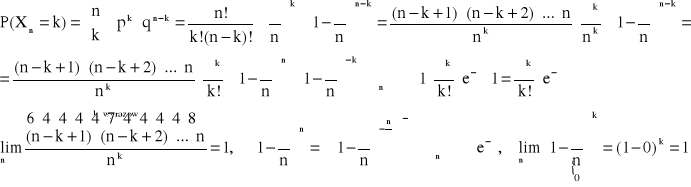
ROZKŁAD GEOMETRYCZNY
Definicja rozkładu geometrycznego:
Mówimy, że zmienna losowa X ma rozkład geometryczny z parametrem p (0 < p < 1) jeśli zmienna ta przyjmuje wartości k z prawdopodobieństwem:
P(X=k) = p · qk-1 , gdzie q=1-p
k=1,2,3,…
0 < p < 1
p + q = 1
0 < q < 1
X |
1 |
2 |
3 |
4 |
… |
k |
… |
P(X=k) |
p |
p · q |
p · q2 |
p · q3 |
… |
p · qk-1 |
… |
P(X=k) > 0
Warunek unormowania:
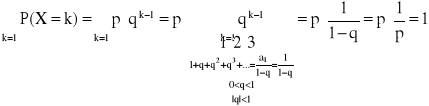
CHARAKTERYSTYKI LICZBOWE ZMIENNYCH LOSOWYCH:
WARTOŚĆ OCZEKIWANA (PRZECIĘTNA) EX, E(X)
Definicja wartości oczekiwanej:
Wartością oczekiwaną zmiennej losowej X:
typu dyskretnego typu ciągłego
nazywamy liczbę
![]()
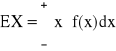
gdzie: gdzie:
W - zbiór punktów skokowych f(x) - gęstość X
przy założeniu, że
szereg ![]()

jest bezwzględnie zbieżny jest bezwzględnie zbieżna
Przykład:
a)
xi |
0 |
1 |
2 |
pi |
|
|
|
E(X) = 0 · ![]()
+ 1 · ![]()
+ 2 · ![]()
= 1
b)
i=1 i=2 i=3
xi |
-2 |
2 |
- |
… |
|
… |
pi |
|
|
|
… |
|
… |
P(Xi) = …
P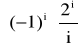
=![]()
Warunek unormowania:
![]()
|q| < 1 ![]()
E(X) = 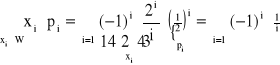
Badamy szereg:
![]()
nie jest zbieżny bezwzględnie ![]()
E(X) nie istnieje
(*) ![]()
- rozbieżny
Przykład:
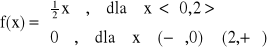
lub:
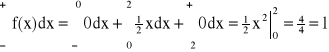
E(X) = 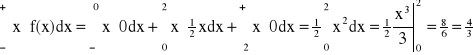
Przykład:
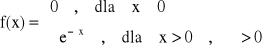
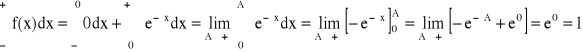
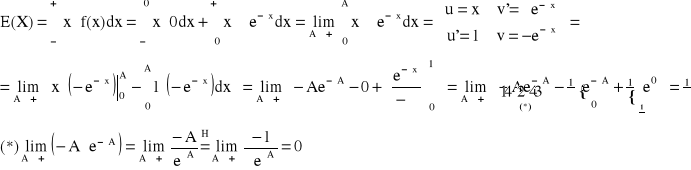
WARIANCJA D2X, D2(X), V(X), VX
Definicja wariancji:
Wariancją (dyspersją) zmiennej losowej X, mającej wartość oczekiwaną nazywamy liczbę:
D2(X) = E(X - E(X))2
(wartość oczekiwana kwadratu różnicy zmiennej losowej X i jej wartości oczekiwanej).
Dla zmiennej losowej typu:
- dyskretnego:
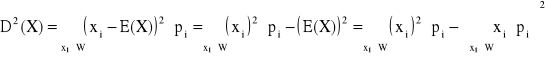
gdzie: W - zbiór punktów skokowych
- ciągłego:
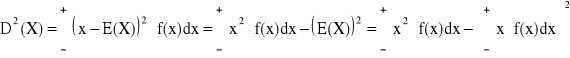
Twierdzenie:
D2(X) = E(X2) - (E(X))2
(różnica wartości oczekiwanej kwadratu zmiennej losowej X2 i kwadratu wartości oczekiwanej zmiennej X)
Z definicji mamy:
D2(X) = E(X - E(X))2 = E(X2 - 2XE(X) + (E(X))2) = E(X2) - E(2XE(X)) + E((E(X))2) =
= E(X2) - 2E(X) · E(X) · E(X) + (E(X))2 = E(X2) - (E(X))2
Przykład:
pi > 0
Σpi = 1
xi |
-1 |
1 |
3 |
pi |
|
|
|
E(X) = x1p1 + x2p2 + x3p3 = -1·![]()
+ 1·![]()
+ 3·![]()
= 1
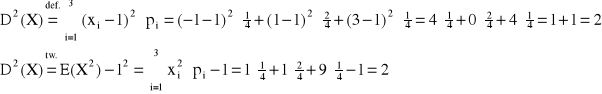
Przykład:
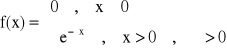
UWAGA: Wariancja nie może być zerem i jest większa od zera!!! D2(X) > 0 0 < pi < 1
PRZYKŁADOWE WARTOŚCI E(X) I D2(X) DLA POSZCZEGÓLNYCH ROZKŁADÓW:
Rozkład |
E(X) |
D2(X) |
Wykładniczy o postaci:
|
|
|
Normalny: N(m,σ) |
m |
σ2 |
|
|
|
Bernoulliego |
n · p |
n · p · q |
Poissona |
λ |
λ |
Geometryczny |
|
|
ELEMENTY KOMBINATORYKI
Kombinacją bez powtórzeń z n elementów po k elementów (k<n) nazywamy zbiór składający się z k różnych elementów wybranych spośród n różnych elementów, przy czym obojętne jest w jakim porządku elementy tego zbioru są rozmieszczone.
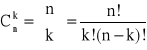
- liczba kombinacji k elementów z n elementów
Przykład:
Ile nastąpi powitań, jeśli jednocześnie spotka się sześciu znajomych?
1, 2, 3, 4, 5, 6 {3,4} = {4,3} k = 2, n = 6
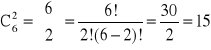
Permutacją bez powtórzeń nazywamy zbiór składający się z n uporządkowanych różnych elementów.
Pn = n! - liczba permutacji
Przykład:
W urnie są 3 kule o numerach: 1,2,3. Wyciągamy po kolei te kule i notujemy ich numery wg
kolejności ich wyciągania (kul nie zwracamy do urny). Ile różnych liczb możemy otrzymać?
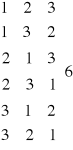
lub: P3 = 3! = 6
Wariancją bez powtórzeń z n elementów po k elementów (k<n)nazywamy zbiór składający się z k różnych elementów wybranych spośród n różnych elementów.
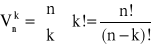
- liczba wariancji bez powtórzeń k elementów z n elementów
Przykład:
Ile można wykonać 3-kolorowych chorągiewek (tylko pasy poziome) z sześciu barw?
n = 6, k = 3
![]()
Wariancją z powtórzeniami z n elementów po k elementów nazywamy uporządkowany zbiór składający się z k elementów różnych lub różniących się między sobą, wybranych spośród n różnych elementów.
![]()
- liczba wariancji z powtórzeniami k elementów z n elementów
Przykład:
Ile można utworzyć 5-cyfrowych liczb z cyfr 4, 5 i 6?
![]()
Twierdzenie:
P(A![]()
B) = P(A) + P(B) - P(A![]()
B) gdzie A,B![]()
Σ
A![]()
B = A![]()
(B-A)
rozłączne
A![]()
(B-A) = ø
P(A![]()
B) = P(A) + P(B-A)
![]()
rozłączne
P(B) = P(A![]()
B) + P(B-A)
P(A) + P(B) - P(A![]()
B)
Przykład:
Obliczyć prawdopodobieństwo tego, że jeśli losujemy 1 kartę z talii 52 kart, to wylosujemy pika lub asa.
52 kart: 13 pików, 4 asy
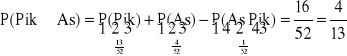
Definicja zdarzeń niezależnych:
Zdarzenia A,B![]()
Σ nazywamy niezależnymi, jeśli P(A![]()
B) = P(A) · P(B).
Załóżmy, że A,B![]()
Σ, P(B)>0
Definicja prawdopodobieństwa warunkowego:
Prawdopodobieństwem warunkowym zajścia zdarzenia A pod warunkiem, że zaszło zdarzenie B, nazywamy liczbę określoną wzorem:
![]()
Zał. P(A)>0, ![]()
P(A![]()
B) = P(A/B) · P(B) = P(B/A) · P(A)
Twierdzenie o prawdopodobieństwie całkowitym (zupełnym):
Jeśli:
zdarzenia A1, A2, …, An

Σ wyłączają się parami Ai
Aj = ø, i≠jA1

A2
…
An = ΩP(Ai) > 0 dla i=1, 2, …, n
to dla każdego zdarzenia B![]()
Σ:
P(B) = P(A1) · P(B/A1) + P(A2) · P(B/A2) + … + P(An) · P(B/An)
DOWÓD:
A1![]()
A2![]()
…![]()
An = Ω
B = B![]()
Ω = B![]()
( A1![]()
A2![]()
…![]()
An) = (B![]()
A1)![]()
(B![]()
A2)![]()
…![]()
(B![]()
An)
P(B) = P(B![]()
A1)+(B![]()
A2)+…+P(B![]()
An) = P(A1)·P(B/A1) + P(A2)·P(B/A2) +…+ P(An)·P(B/An)
Przykład:
Trzy maszyny produkują pewien towar:
I maszyna: 50 sztuk: średni % braków = 3%
II maszyna: 30 sztuk: średni % braków = 4%
III maszyna: 20 sztuk: średni % braków = 5%
Obliczyć prawdopodobieństwo trafienia na brak w całej produkcji.
P(B) = P(A1) · P(B/A1) + P(A2) · P(B/A2) + P(A3) · P(B/A3)
i=1,2,3
P(Ai) - prawdopodobieństwo trafienia na towar wyprodukowany przez i-tą maszynę
P(B/Ai) - prawdopodobieństwo trafienia na brak pod warunkiem, że towar pochodzi z i-tej
maszyny
![]()
Twierdzenie Bayesa (o prawdopodobieństwie a posteriori):
Jeśli:
zdarzenia A1, A2, …, An

Σ wyłączają się parami Ai
Aj = ø, i≠jA1

A2
…
An = ΩP(Ai) > 0 dla i=1, 2, …, n
to dla każdego zdarzenia B![]()
Σ takiego, że P(B)>0 zachodzi wzór BAYESA:
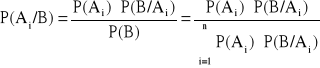
(prawdopodobieństwo zajścia zdarzenia Ai pod warunkiem, że B już zaistniało)
bo:
![]()
Przykład:
(drugie pytanie do w/w zadania).
Przypuśćmy, że wylosowano jedną sztukę produkcji i okazała się ona brakiem. Jakie jest prawdopodobieństwo, że brak ten wyprodukowała trzecia maszyna?
![]()
Przykład:
W urnie jest 5 kul białych i 10 czarnych. Losujemy kolejno bez zwracania 2 kule. Jakie jest prawdopodobieństwo, że za drugim razem wylosujemy kulę białą?
![]()
Opis:
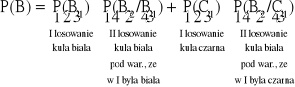
18
x
y
y=f(x)
![]()
![]()
x
y
y
x
y=F(x)
1
2
F(1) = 0 , F(2) = 1
1
0
y
x
y = f(x)
![]()
![]()
y = F(x)
x
y
0
y
x
c
a
b
x
b
a
1
y
y = F(x)
y
x
m
m - σ
m + σ
p2
P
p1
x
y
xn
x1
x2
X
pn
X
X
x2
x1
xn
X
q
P
x1
x2
p+q = 1
p
P
x1
x2
p
P
y = F(x) - funkcja ciągła
2
X
2
1
3 4
1
X
P
1 2 3 4
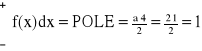
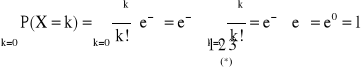
P
y=![]()
x
1
b
a
![]()
![]()
A-B
A![]()
B
B
A
10C
5B
B
B
B
C
C
C
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Matematyka - rachunek prawdopodbieństwa - ściąga, szkoła
09 Rachunek prawdopodobie ästwaid 7992
7 ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA
MATEMATYKA Rachunek prawdopodobieństwa, str tytułowa, Marcin Nowicki
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka dzienne wyklad1, Rachunek prawdopodobie˙stwa
1 zadania z rachunku prawdopodobieństwa, Zad
Zestaw10 rachunek prawdopodobie Nieznany
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 18.05.2008
rachunek prawdopodobieństwa, rachl4
kolokwia, KOLO1 01, KOLOKWIUM POPRAWKOWE Z RACHUNKU PRAWDOPODOBIE˙STWA& MATEMATYKI FINANSOWEJ UW
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 11.05.2008
Statystyka dzienne wyklad4, Rachunek prawdopodobie˙stwa
więcej podobnych podstron