Gliwice, 26.10.1995 r

Laboratorium z fizyki

Temat: Dyfrakcja światła

ćwiczenie nr 9

Aleksandra Poloczek

Michał Krzemień

MT gr I I , sekcja 8

1. Temat ćwiczenia:

Dyfrakcja światła

2 Wprowadzenie:

Dyfrakcja fali (ugięcie fali) jest w szerokim sensie zespołem zjawisk związanych z odstępstwami od praw optyki geometrycznej podczas rozchodzenia się fal w ośrodkach niejednorodnych. W większym znaczeniu dyfrakcja fal jest pewnym odstępstwem od praw geometryki geometrycznej przy rozprzestrzenianiu się fal lokalnie płaskich w ośrodkach jednorodnych. W skutek dyfrakcji pojawiają się dodatkowe kierunki rozchodzenia się fal, nie przewidziane przez optykę geometryczną. Zjawisko dyfrakcji jest charakterystyczne dla wszystkich rodzajów fal, jednak możliwość obserwacji dyfrakcyjnych maleje ze wzrostem częstotliwości.

2.1 Doświadczenie Younga:

Światło lampy ługowej przechodzi przez szczelinę szerokości 0.25 [mm] i pada na ekran dwoma otworami o średnicy 0.1 [mm] i rozsuniętymi o 0.7 [mm]. Na ekranie odległym o 5 [m] obserwuje się wynik interferencji fal kulistych. Szczelinę tą można potraktować jako źródła drgające synchronicznie więc różnica faz dwóch fal docierających do punktu A jest wynikiem różnicy przebytej drogi.

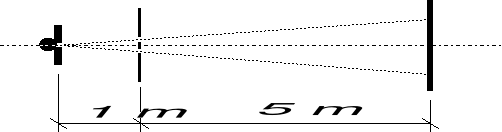
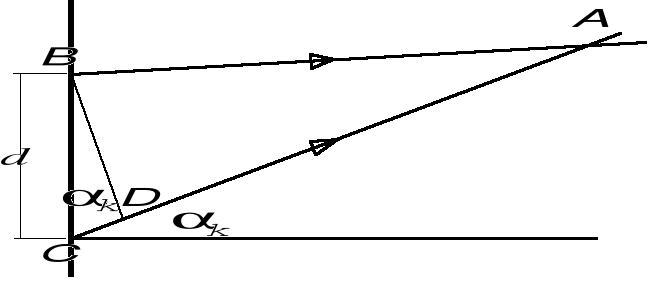
Wzmocnienie fal zajdzie wówczas, gdy różnica faz wyniesie 2k.

Warunek wzmocnienia:

k - liczba całkowita, rząd prążka interferencyjnego

d - odległość między szczelinami

Wzajemne wygaszenie fal wystąpi gdy:

2.2 Interpretacja Younga:

Powstawanie fal ugiętych ma charakter lokalny i zachodzi w okolicy granicy cienia za krawędzią przesłony lub obszarze oświetlonym. W pierwszym przypadku ugięcie wystąpi wskutek przekazywania amplitudy drgań wzdłuż walcowych powierzchni falowych za granicą cienia. W przypadku drugim fale walcowe wysyłane są z brzegu otworu.

Celem poglądowego przedstawienia dyfrakcji w punkcie A za otworem Frensnel wprowadził podział płaszczyzny otworu na pierścieniowe, półfalowe strefy. Promienie tych sfer dobiera się tak, aby odległości kolejnych okręgów od punktu A różnimy się o połowę długości fali.

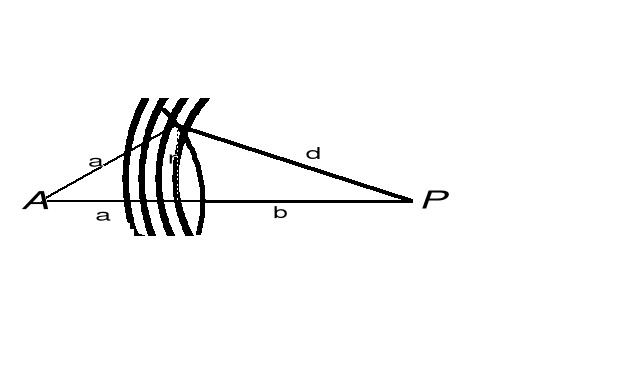
Promień k-tej strefy oblicza się stosując wzór Pitagorasa:

ponieważ x jest znacznie mniejsze od a.

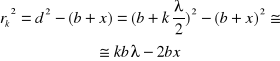
Porównując prawe strony równań:

Ostateczny wzór na promień k-tej strefy wynosi:

Amplituda k-tej strefy zależy od k, ponieważ:

- odległości stref od źródła wzrastają, więc amplitudy powoli maleją,

- wzrasta nachylenie promienia do powierzchni strefy i zmniejsza się natężenie promieniowania,

- amplituda zależy od powierzchni strefy.

Wpływ czynnika pierwszego dokładnie równoważy działanie czynnika trzeciego, więc;

A1>A2>A3>

Zmiany są niewielkie i dla sąsiednich stref zachodzi:

Natężenie fali zależy więc jedynie od amplitudy pierwszej strefy, bowiem: A = A1 / 2

2.1 Wyznaczanie stałej siatki dyfrakcyjnej.

Zjawiska dyfrakcyjne można podzielić na dwie grupy zależnie od odległości szczeliny od źródła i ekranu. Jeśli jedna z nich jest skończona, to mamy do czynienia z dyfrakcją Fresnela.

Dyfrakcja Fraunhofera zachodzi wówczas, gdy zarówno źródło jak i ekran są w nieskończenie wielkich odległościach od szczeliny. Dyfrakcję zaobserwujemy tylko przy zastosowaniu soczewki skupiającej ustawionej w odległości ogniskowej od ekranu.

Stałą siatki dyfrakcyjnej nazywamy sumę szerokości szczelin (a) siatki i ich wzajemnego rozmieszczenia (b), i oznaczamy ją symbolem (d).

d = a + b

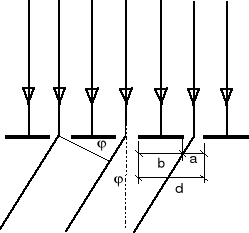
Schemat siatki dyfrakcyjnej.

Natężenie prążków uzyskiwanych w siadce dyfrakcyjnej zależy od kwadratu całkowitej liczby szczelin N i rzędu prążka, i tak dla prążka centralnego mamy:

gdzie C - współczynnik proporcjonalności.

Natężenia poszczególnych prążków są coraz słabsze:

Zdolność rozszczepiania jest miarą jakości siatki i wyraża jest wzorem:

Ćwiczenie nr 1.

Wyznaczanie stałej siatki dyfrakcyjnej

Tabela pomiarowa

	n = 1			n = 2			n = 3
	1l [ ' ]	1p [ ' ]	2l [ ' ]	2p [ ' ]	3l [ ' ]	3p [ ' ]
1	420	360	740	760	1240	1180
2	400	340	820	760	1240	1180
3	400	360	820	760	1240	1200
4	400	360	820	760	1240	1180
5	400	360	820	760	1240	1180
średni kąt	380			782			1212

Tabela błędów kąta:

Kąt	przeciętny [ ' ]	maksymalny [ ' ]	przeciętny średniej [ ]	względy
1	24	40	13.85641	0.000608
2	30,4	42	17.55145	0.00077
3	28	32	16.16581	0.000709

Stała siatki dyfrakcyjnej:

gdzie: l = 583.9 nm - średnia wartość długości fali żółtego dubletu sodu.

n - rząd prążka dyfrakcyjnego

Dla poszczególnych średnich kątów wartość stałej siatki dyfrakcyjnej wynosi:

d1= 5.29 . 10-3 [ mm ]

d1= 5.18 . 10-3 [ mm ]

d1= 5.07 . 10-3 [ mm ]

Średnia ważona:

Stała: a = 1.0 . 10-6

Wagi: w1 = 2.71

w2 = 2.71

w3 = 2.71

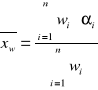
Średnia ważona wynosi: 0.005194 [ mm ]

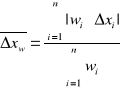
Błąd średniej ważonej wynosi: 0.000682 [ mm ]

Ostateczna wartość stałej siatki dyfrakcyjnej wynosi :

d = (5.19 0.68). 10-3 [ mm ]

Ćwiczenie nr 2

Odległość siatki od ekranu l = 1180 mm

n	x [ mm ]			Xn
	lewo	prawo	[ mm ]
1	150	149	149.5
2	304	312	308
3	473	495	484

Tabela błędów

Pomiar	preciętny [ mm ]	maksymalny [ mm ]	przeciętny średniej [ mm ]	względy [ mm ]
1	0.5	0.5	0.288675	0.001931
2	4	4	2.309401	0.007498
3	5	5	2.886751	0.005964

Obliczamy długość światła laserowego dla poszczególnych pomiarów n :

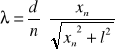
1 = 653 . 10-6 [ mm ]

1 = 655 . 10-6 [ mm ]

1 = 656 . 10-6 [ mm ]

Po przeprowadzeniu analogicznych obliczeń średnia długość światła laserowego wynosi:

= (655 12 ) 10 -6 [ mm ]

Ćwiczenie nr 3

Tabela pomiarowa

Odległość szczeliny od ekranu 1 = 42.7 cm

Położenie środka centrlnego xo = 40.45 mm

n	xo [ mm ]
	lewo	prawo
1	2.08	2.397
2	4.28	4.479
3	6.699	5.514

Tabela błędów

Pomiar	przeciętny [ mm ]	maksymalny [ mm ]	przeciętny średniej [ mm ]	względy [ mm ]
1	0.1585	-0.1585	0.1585	0.04088
2	0.1	-0.1	0.1	0.013182
3	-0.595	0.595	0.595	0.056269

Korzystając ze wzoru:

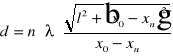
obliczamy szerokość szczeliny d dla każdego prążka:

d1= 7.35 . 10-3 [ mm ]

d1= 7.78 . 10-3 [ mm ]

d1= 8.17 . 10-3 [ mm ]

Po obliczeniu średnich wartości i przeprowadzeniu dyskusji błędów szerokość szczeliny jest równa:

d = ( 7.76 0.23 ) . 10-5 [ mm ]

Wnioski:

Trzy przeprowadzone powyżej ćwiczenia są ściśle ze sobą powiązane. Bardzo ważną cechą tych badań jest to by pomiary przeprowadzać bardzo starannie ponieważ wymiary mierzone są rzędu 10-6 10-5 mm. Bardzo przydatnym narzędziem pracy jest w tym przypadku komputer, który wykorzystany został do przeprowadzenia doświadczenia wyznaczenia szerokości szczeliny siatki dyfrakcyjnej.

---