Zależność korelacyjna- polega ona na tym, że określonym wartościom jednej zmiennej odpowiadają ściśle określone średnie wartości drugiej zmiennej. Możemy zatem ustalić jak zmieni się wartość zmiennej zależnej (Y) w zależności do wartości średniej niezależnej (X).
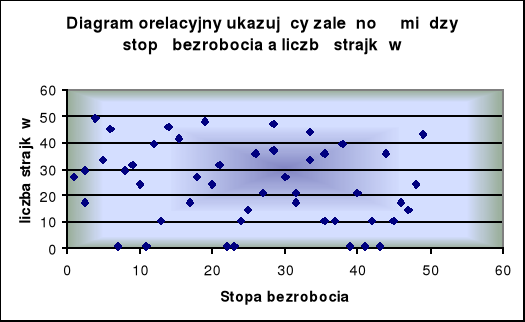
Poniżej przedstawiony został wykres zależności między stopą bezrobocia a ilością strajków. Wyraźnie widać, że zależność korelacyjna nie występuje lub jest bardzo niska.
Wykres 1
Dla zbadania korelacji skorzystam ze współczynnika korelacji rang Spearmana.
Rs=1- 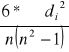
Dane potrzebne do obliczeń zostały umieszczone w tabeli nr 1:
Tabela nr 1
xi |
yi |
di=xi-yi |
di2 |
1 |
27 |
-26 |
676 |
2,5 |
17,5 |
-15 |
225 |
2,5 |
29,5 |
-27 |
729 |
4 |
49 |
-45 |
2025 |
5 |
33,5 |
-28,5 |
812,3 |
6 |
45 |
-39 |
1521 |
7 |
1 |
6 |
36 |
8 |
29,5 |
-21,5 |
462,3 |
9 |
31,5 |
-22,5 |
506,3 |
10 |
24 |
-14 |
196 |
11 |
1 |
10 |
100 |
12 |
39,5 |
-27,5 |
756,3 |
13 |
10,5 |
2,5 |
6,25 |
14 |
46 |
-32 |
1024 |
15,5 |
41,5 |
-26 |
676 |
15,5 |
41,5 |
-26 |
676 |
17 |
17,5 |
-0,5 |
0,25 |
18 |
27 |
-9 |
81 |
19 |
48 |
-29 |
841 |
20 |
24 |
-4 |
16 |
21 |
31,5 |
-10,5 |
110,3 |
22 |
1 |
21 |
441 |
23 |
1 |
22 |
484 |
24 |
10,5 |
13,5 |
182,3 |
25 |
14,5 |
10,5 |
110,3 |
26 |
36 |
-10 |
100 |
27 |
21 |
6 |
36 |
28,5 |
37 |
-8,5 |
72,25 |
28,5 |
47 |
-18,5 |
342,3 |
30 |
27 |
3 |
9 |
31,5 |
21 |
10,5 |
110,3 |
31,5 |
17,5 |
14 |
196 |
33,5 |
44 |
-10,5 |
110,3 |
33,5 |
33,5 |
0 |
0 |
35,5 |
36 |
-0,5 |
0,25 |
35,5 |
10,5 |
25 |
625 |
37 |
10,5 |
26,5 |
702,3 |
38 |
39,5 |
-1,5 |
2,25 |
39 |
1 |
38 |
1444 |
40 |
21 |
19 |
361 |
41 |
1 |
40 |
1600 |
42 |
10,5 |
31,5 |
992,3 |
43 |
1 |
42 |
1764 |
44 |
36 |
8 |
64 |
45 |
10,5 |
34,5 |
1190 |
46 |
17,5 |
28,5 |
812,3 |
47 |
14,5 |
32,5 |
1056 |
48 |
24 |
24 |
576 |
49 |
43 |
6 |
36 |
|
|
|
24895 |
R = - 0,27
Świadczy to o niskim ujemnym wspólczynniku korelacji
Współczynnik determinacji R2 - określa jaki procent zmienności zmiennej zależnej jest wywołany kształtowaniem zmiennej niezależnej.
R2=Rs* Rs * 100%
R2= 7,29%
ϕ2 = 1 - R2
ϕ2 = 92,71%
Tylko 7,29% strajków było uzasadnione stopa bezrobocia w poszczególnych województwach Polski w 1994 roku. Natomiast 92,71% liczby strajków nie jest wyjaśnione stopą bezrobocia.
Nastęnie sprawdzę czy związek między liczbą strajków a stopą bezrobocia jest staystycznie istotny na poziomie istotności α = 0,05.
H0:ρs=0
H1:ρs![]()
0
Do weryfikacji hipotezy zerowej wykorzystujemy statystykę:
Dla prób o n≥10 rozkład współczynnika korelacji rang jest normalny o parametrach N(0,![]()
). Dlatego też test weryfikujący hipotezę zerową jest w takich przypadkach oparty na statystyce z o rozkładzie normalnym N(0,1):
zs=![]()
zs= - 1,87
Na poziomie istotności α = 0,05 z przyjmuje wartość 1,96, a więc zs < z, stąd wnisek, że nie ma podstaw do odrzucenia hipotezy zerowej, czyli związek nie jest statystycznie istotny.
Podsumowanie:
Dzięki otrzymanym wyliczeniom możemy stwierdzić, że pomiędzy liczbą strajków a stopą bezrobocia w poszczególnych województwach zachodzi słaby ujemny związek korelacyjny o sile -0,27. W 7,29% zmiany w powierzchni gruntów leśnych wpływają na średnie zmiany w liczbie saren leśnych w poszczególnych województwach w 1994. Brak podstaw do odrzucenia hipotezy zerowej pozwoliło stwierdzić, iż związek pomiędzy liczbą strajków a stopą bezrobocia w poszczególnych województwach nie jest statystycznie istotny.
Wyszukiwarka
Podobne podstrony:
zadania korelacje2now
Zadania-korelacjaX, Informatyka i Ekonometria SGGW, Semestr 2, Statystyka opisowa i ekonomiczna, zad
statystyka zadania korelacja i regresja
6 Zadania z a korelacji (krotkie) ROZWIAZAC
5 Zadania z a korelacji (Spearman & Pearson)
zadanie 1- zmienne i zaleznosci miedzy nimi, Statyst. zadania
Zadaniedo8 ćwiczenia KORELACJA, Rok I, matematyka
zadania na korelację, Statystyka
6 regresja kowariancja korelacja zadania
FiR-przykladowe zadania z dynamiki i korelacji, Finanse i rachunkowość, 3 semestr, statystyka
Zadania na korelacje Pearsona Spearmana
Zadanie 03 korelacja, Niezawodność konstr, niezawodność, 1 projekt
Przyklady do rozwiazania - tablica korelacyjna, Informatyka i Ekonometria SGGW, Semestr 2, Statystyk
6 regresja kowariancja korelacja zadania
zadanie na korelację, Statystyka
statystyka ćw, korelacja - zadania Zarz+Soc, Zadanie 2
więcej podobnych podstron