Wykład 5

Teoria produkcji - decyzje producenta w warunkach pewności: problem maksymalizacji zysku

1. Zarys problemu

W tradycyjnej teorii neoklasycznej przedsiębiorstwo rozumiane jest jako jednostka, która przekształca nakłady czynników produkcji w dobra i usługi wykorzystując w tym celu pewien proces produkcyjny (technologiczny). Dla uproszczenia załóżmy, że przedsiębiorstwo wytwarza jednorodny produkt w ilościach
zużywając w tym celu
czynników
.

Planem produkcyjnym przedsiębiorstwa nazwiemy taki wektor
, gdzie
. Pan produkcyjny nazwiemy wykonalnym jeśli
.
jest funkcją produkcji. Funkcja ta określa maksymalną wielkość produkcji możliwą do wykonania z każdej dostępnej przedsiębiorstwu kombinacji nakładów czynników produkcji. Plan produkcyjny będzie wykonalny wtedy i tylko wtedy, gdy należy do takiego zbioru produkcyjnego
, który

.

Załóżmy dalej, że przedsiębiorstwo wynajmuje czynniki produkcji i sprzedaje produkt na rynkach po cenach równych odpowiednio
i
(
), na które nie ma wpływu. Wykonanie planu produkcyjnego
jest związane z poniesieniem kosztów
i prowadzi, po sprzedaży produktu, do osiągnięcia przychodu równego
. Zyskiem przedsiębiorstwa jest więc
.

Załóżmy dalej, że przedsiębiorstwo określa swój plan produkcyjny w taki sposób, aby zmaksymalizować zysk przy danej technologii wytwarzania. Problemem przedsiębiorstwa jest więc

przy ograniczeniu
,

gdzie
. Założenie, że
oznacza dopuszczenie możliwości istnienia takiego planu produkcji, dla którego niektóre elementy mogą być zerowe. Tymczasem interesują nas rozwiązania wewnętrzne, czyli takie, dla których
. Dalej będziemy więc zakładać, że problemem przedsiębiorstwa jest

przy ograniczeniu
,

gdzie
.

2. Warunki konieczne i dostateczne istnienia maksimum zysku

Funkcją Lagrange'a dla problemu przedsiębiorstwa jest

.

Warunki Kuhna-Tuckera dla tego problemu są następujące:

,

,

.

Z warunków tych wynika, że
oraz:

• 
  ,
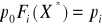
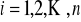
  oraz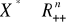
  (wartość produktywności krańcowej nakładu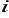
  -tego czynnika produkcji jest równa cenie jednostki tego czynnika),

• 
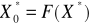
  (przedsiębiorstwo produkuje na funkcji produkcji).

Dla
rozwiązanie problemu przedsiębiorstwa zobrazowano na poniższym rysunku.

3. Funkcje podaży produkcji, popytu na czynniki produkcji, zysku

Rozwiązując problem przedsiębiorstwa otrzymamy:

• funkcje rozwiązania
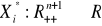
  przyjmujące wartości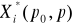
  ,
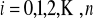
  ; funkcją podaży produkcji jest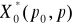
  , funkcjami popytu na czynniki produkcji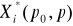
  ,
  ;

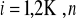
• funkcję zysku
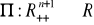
  przyjmującą wartości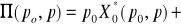
  
  ;

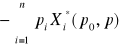
• funkcję mnożnika
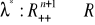
  przyjmującą wartości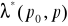
  .

Przykład.

Niech funkcją produkcji jest
, gdzie
(funkcja Cobb-Douglasa). Wówczas zyskiem przedsiębiorstwa jest
. Problem przedsiębiorstwa można więc zapisać jako

przy ograniczeniu
,

gdzie
. Funkcją Lagrange'a dla tego problemu jest

,

a warunkami Kuhna-Tuckera:

,

,

.

Z warunków tych wynika, że

oraz
.

Stąd:

,

(wielkość produkcji maksymalizująca zysk przy cenach
),

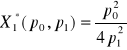
(wielkość nakładu czynnika produkcji maksymalizująca zysk przy cenach

),

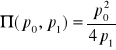
(maksymalny zysk przy cenach
),

.

Twierdzenie Hotellinga.

Niech funkcja produkcji
spełnia wszystkie powyżej sformułowane własności oraz
jest
,
,
jest
,
jest
. Wówczas :

• 
  ,

• 
  ,

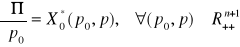
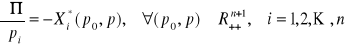
Dowód:

Funkcją Lagrange'a dla problemu przedsiębiorstwa jest

.

Różniczkując ją po
i
otrzymamy odpowiednio
i
. Kładąc
oraz
otrzymamy cbdo.

Funkcja zysku jest funkcją wklęsłą.

Przykład c.d.

Funkcją zysku dla problemu przedsiębiorstwa z funkcją produkcji
, gdzie
, jest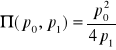
. Stąd
oraz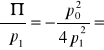

.

4. Własności funkcji zysku, funkcji podaży produkcji oraz funkcji popytu na czynniki produkcji

Macierz drugich pochodnych cząstkowych funkcji zysku,
, jest macierzą półdodatnio określoną, czyli taką, że wszystkie minory główne
-tego rzędu
są dla
nieujemne (funkcja zysku jest funkcją wklęsłą).

Z twierdzenia Hotellinga wynika, że

.

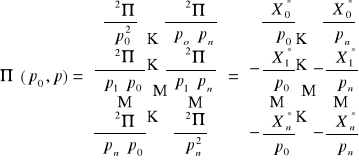
Macierz

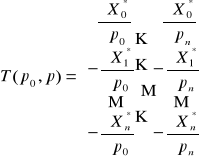
jest półdodatnio określona i symetryczna dla wszystkich
.

Twierdzenie.

Niech funkcja produkcji
spełnia wszystkie powyżej sformułowane własności. Wówczas:

• 
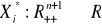
  jest funkcją jednorodną rzędu zerowego dla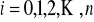
  ;

• 
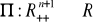
  jest funkcją jednorodną rzędu pierwszego.

Dowód:

(a) Plan produkcyjny
jest rozwiązaniem problemu przedsiębiorstwa przy cenach
wtedy i tylko wtedy, gdy
,
,
oraz
. Stąd dla
, gdzie
,
jest rozwiązaniem problemu przedsiębiorstwa wtedy i tylko wtedy, gdy
,
,
oraz
. Stała
występuje po obu stronach równania
, zatem
jest rozwiązaniem zarówno dla
, jak i
. Zatem dla każdego
można zapisać, że
oraz
.

(b) Mamy
. Stąd dla każdego

.

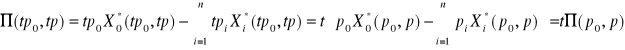
Wniosek z powyższego twierdzenia:

Korzystając z twierdzenia Eulera dla wszystkich
oraz
mamy

.

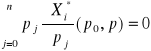
5. Analiza statyki porównawczej

Dla
mamy

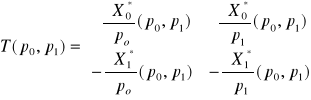
oraz

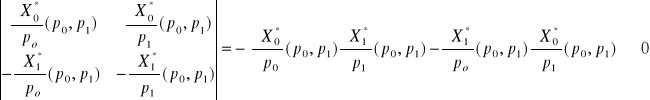
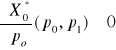
(wielkość produkcji wzrasta wraz ze wzrostem ceny jednostkowej

produktu, ceteris paribus),

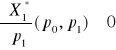
(nakład czynnika produkcji zmniejsza się wraz ze wzrostem jego ceny

jednostkowej, ceteris paribus).

Z twierdzenia Eulera mamy ponadto:

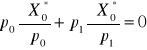
oraz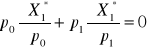
.

Stąd:

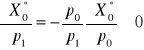
(wielkość produkcji maleje wraz ze wzrostem ceny jednostkowej

nakładu czynnika produkcji, ceteris paribus),

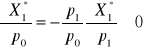
(nakład czynnika produkcji wzrasta wraz ze wzrostem ceny

jednostkowej produktu, ceteris paribus).

Jak kształtują się mnożniki w przypadku ogólnym?

Zadania do samodzielnego rozwiązania

(Paul Madden, Concavity and Optimization in Microeconomics. Basil Blackwell, Oxford 1986, s.149-50):

1. Dla funkcji produkcji Cobb-Douglasa,
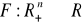
   , takiej że:

pokaż iż:

• 
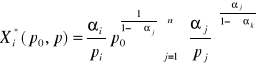
  jest funkcją popytu na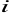
  -ty czynnik

produkcji

• 
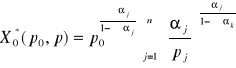
  jest funkcją podaży produkcji

• 
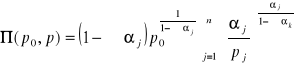
  jest funkcją zysku.

• Sprawdź, że zachodzą następujące związki (twierdzenie Hotellinga):

,

.

• Pokaż, że funkcje popytu na czynniki produkcji oraz podaży produkcji można zapisać w postaci:

.

Określ postacie
oraz
.

• Zinterpretuj
  .

• Pokaż, że elementy znajdujące się w macierzy
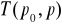
  poza główną przekątną są ujemne.

2. Rozważ funkcję produkcji CES,
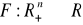
   , taką że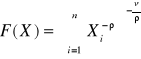
   , gdzie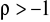
   ,
   oraz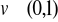
   i pokaż, że:

• 
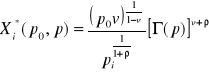
  , gdzie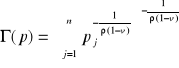
  .

• Pokaż, że

jest funkcją podaży produkcji, natomiast

- jest funkcją zysku,

a wszystkie elementy macierzy
poza główną przekątna są ujemne.

Paweł Miłobędzki: Wykłady z ekonomii matematycznej

1

2

---