1.
Opór obciążenia liczymy bezpośrednio z prawa Ohma wykorzystując wzór R=U/I.
Moc obliczamy z wzoru Pu=UI.
Moc całkowitą obliczam z wzoru P=εI
sprawność η z zależności η=Pu/P
2.
Wykres zależności U=f(I) wraz z aproksymacją.
Wykres zależności U(I) jest liniowy. Można opisać go równaniem f(x) = ax +b, gdzie w naszym przypadku U(I) = ε - Ir a = r, b = ε. Do wyznaczenia a i b posłużyłem się metoda regresji liniowej (obliczone wartości znajdują się w tabelce).
r= 222,3 ohm
ε = 2,72 V
3.
Do wyznaczenia błędu pomiaru Δε i Δr skorzystam z metody najmniejszych kwadratów.
![]()
![]()
W tym celu należy policzyć
(gdzie a = -0,223 ; b=2,92 )
Błąd Δε wynosi
U(a) = 0,15 [V]
natomiast Δr
u(b) = 0,0012 ohm
Z wykresu zależności Pu(R/r) wynika, że moc użyteczna osiąga wartość maksymalną dla oporu zewnętrznego bliskiego oporowi wewnętrznemu źródła zasilania (R/r = 0,91) Dla powyższej wartości oporu odbiornika sprawność η=0,35. Można się domyślić, że Pu osiągnie wartość maksymalna dla R/r = 1, a sprawność dla tak zestawionego układu będzie równa 0,5.
Z ćwiczenia wynika, że największą moc użyteczną można otrzymać dla odbiornika o oporze wewnętrznym równym oporowi wewnętrznemu źródła zasilania.
Ponadto można zauważyć, że największa sprawność jest osiągana dla małych prądów i spada ona wraz ze wzrostem prądu.
Duży spadek sprawności przy większym natężeniu wynika ze strat energii na oporze wewnętrznym źródła zasilania. Aby unikać takich strat należy budować źródła zasilania o oporze wewnętrznym dopasowanym do docelowego odbiornika złe dopasowanie wiąże się z tym niebezpieczeństwo, że podczas zwarcia w obwodzie popłynie bardzo duży prąd, bądź źródło zostanie bardzo szybko rozładowane.
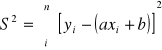
![]()
Wyszukiwarka
Podobne podstrony:
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
8 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
[10]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[8]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
cw 11- opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowaniemoje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
10 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[3]opracowaniemoje (2), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
[9]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Opracowanie11, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
11 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
8 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, Sprawozdan
Opracowanie6, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, la
Opracowanie05, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
[6]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
opracowanie cw 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
więcej podobnych podstron