Opracowanie wyników:
I - badany gaz powietrze
1. Na podstawie pomiarów dla każdej częstotliwości obliczam średnią długość fali:
f [Hz] |
1/f [s] |
Położenie słupa wody w rezonansie λ/2 [m] |
λśr/2 [m] |
λśr [m] |
700 |
0,001429 |
0,190 0,430 0,670 0,910 |
0,240 |
0,480 |
700 |
0,001429 |
0,190 0,420 0,670 0,910 |
0,240 |
0,480 |
800 |
0,00125 |
0,065 0,280 0,490 0,710 0,930 |
0,216 |
0,432 |
800 |
0,00125 |
0,060 0,270 0,490 0,710 |
0,216 |
0,432 |
900 |
0,00111 |
0,175 0,370 0,555 0,740 0,930 |
0,189 |
0,378 |
900 |
0,00111 |
0,170 0,355 0,560 0,750 |
0,193 |
0,386 |
1000 |
0,001 |
0,090 0,255 0,430 0,600 0,775 |
0,171 |
0,342 |
1000 |
0,001 |
0,080 0,250 0,430 0,600 0,770 |
0,173 |
0,346 |
2. Tabelka 1/f oraz λśr , dla której sporządzam wykres wraz z zaznaczeniem niepewność pomiarowych:
1/f [Hz] |
λśr [m] |
0,001429 |
0,480 |
0,00125 |
0,432 |
0,00111 |
0,382 |
0,001 |
0,344 |
Wykres zależności 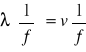
dla powietrza.
λ w funkcji (1/f) jest prostą o współczynniku kierunkowym V i wyrazie wolnym =0. Wykres w tym układzie osi przedstawiono na rys:
Niepewności λ zawierają się w „grubo*ci” punktu (tak jak na rysunku powyżej).
Prostą λ=a*(1/f) +b dopasowuje się metod* najmniejszych kwadrat*w (tj. tak dobiera się prostą, aby suma odległości od niej do wszystkich punkt*w doświadczalnych by*a minimalna).
Odpowiednie wzory na współczynniki dopasowania mają postać:
![]()
,
gdzie: 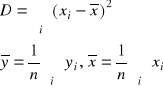
w tym przypadku:
a=318,9
b=0,028
3. Ze współczynnika nachylenia prostej wyliczam prędkość dźwięku:
Prędkość dźwięku równa jest współczynnikowi nachlania prostej λ=a*(1/f) +b
V = 318,9± 0,9 [m/s],
gdzie niepewność została obliczona na podstawie odchylenia standardowego parametrów dopasowania prostej ze wzorów:
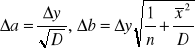
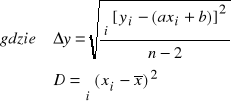
Δa =0,9
4. Obliczenie współczynnika κ i oszacowanie jego niepewności:
κ=cp/cv Korzystamy ze wzorów na prędkość dźwięku na podstawie praw gazowych Wtedy
Używając danych tablicowych R i μ oraz wielkości zmierzonych V, T dostajemy:
μ=29g/mol,
R=8.314J/mol*K,
V=319 m/s,
T=21oC = 273+21[K] =294 [K]
Więc κ=1,207
5. Wyznaczam liczbę stopni swobody molekuł gazu ze wzoru:
a więc i=2/(κ-1)
po obliczeniu i = 9
6. Niepewności pomiarowe:
długość fali:
ze wzorów
oraz
dla f=700Hz
λ={ 0,48 0,48}
λśr = 0,48
S(λśr) = 0
Dla f=800Hz
λ={ 0,432 0,432}
λśr = 0,432
S(λśr) = 0
Dla f=900Hz
λ={ 0,378 0,386}
λśr = 0,382
S(λśr) = 0,004
Dla f=1000Hz
λ={ 0,342 0,346}
λśr = 0,344
S(λśr) = 0,002
b)częstotliwość:
niepewność liczymy ze wzoru:
ΔT = | dT/df| * |Δf|
dla f=700 Hz Δ1/f =0.00002 s
dla f=800 Hz Δ1/f = 0.0000156 s
dla f=900 Hz Δ1/f =0,0000123 s
dla f=1000 Hz Δ1/f = 0.000001 s
7.Obliczenie niepewności pomiarowych prędkości dźwięku metodą najmniejszych kwadratów:
Korzystając z wzorów:
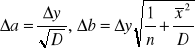
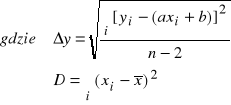
Δa =0,9
Więc: V = 318,9± 0,9 [m/s]
8. Porównuje liczbę stopni swobody z wielkością teoretyczna:
|
Wartość teoretyczna |
Wartość wyznaczona |
Współczynnik κ |
1,4 |
1,207 |
Liczba stopni swobody i |
5 |
9 |
Obliczona liczba stopni swobody w przypadku powietrza znacznie odbiega od wartości teoretycznej. W tym doświadczeniu trudno jest uzyskać dużą dokładność liczby stopni swobody, ponieważ sposób obliczania wymaga bardzo dokładnego wyznaczenia prędkości dźwięku w gazie. We wzorze na współczynnik ![]()
prędkość jest podnoszona do kwadratu, a następnie obliczony współczynnik jest wykorzystywany w zależności na liczbę stopni swobody, w której niewielkie zmiany ![]()
przekładają się na duże zmiany ![]()
.
II Badany gaz CO2
Wszystkie punkty liczę według tych samych wzorów co w punkcie I.
1. Na podstawie pomiarów dla każdej częstotliwości obliczam średnia długość fali:
f [Hz] |
1/f [s] |
Położenie słupa wody w rezonansie λ/2 [m] |
λśr/2 [m] |
λśr [m] |
700 |
0,001429 |
0,130 0,330 0,525 0,730 0.930 |
0,200 |
0,400 |
800 |
0,00125 |
0,230 0,405 0,590 0,760 |
0,177 |
0,354 |
1000 |
0,001 |
0,150 0,280 0,410 0,545 0,655 0,825 |
0,135 |
0,270 |
2. Tabelka 1/f oraz λśr dla której sporządzam wykres wraz z zaznaczeniem niepewność pomiarowych
1/f [Hz] |
λśr [m] |
0,001429 |
0,4 |
0,00125 |
0,354 |
0,001 |
0,27 |
Wykres zależności 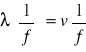
dla dwutlenku węgla
Niepewności λ zawierają się w „grubo*ci” punktu (tak jak na rysunku powyżej).
Prostą λ=a*(1/f) +b dopasowuje się metod* najmniejszych kwadrat*w (tj. tak dobiera się prostą, aby suma odległości od niej do wszystkich punkt*w doświadczalnych by*a minimalna).
Dopasowanie krzywej teoretycznej do wykresu wynik*w doświadczalnych:
a=305,1
b=-0,3
3. Ze współczynnika nachylenia prostej wyliczam prędkość dźwięku:
Prędkość dźwięku równa jest współczynnikowi nachlania prostej λ=a*(1/f) +b
V = 305,1 ± 1 [m/s],
Δa =1
4. Obliczenie współczynnika κ i oszacowanie jego niepewności:
μ=44g/mol,
R=8.314J/mol*K,
V=260 m/s,
T=21oC = 273+21[K] =294 [K]
Wtedy:
κ=1,676
5. Wyznaczam liczbę stopni swobody molekuł CO2 : i= 3
6. Niepewności pomiarowe:
a) długość fali:
dla f=700Hz
λ={ 0,4 0,39 0,41 0,4 }
λśr = 0,4
S(λśr) = 0,004
Dla f=800Hz
λ={ 0,35 0,37 0,34}
λśr = 0,354
S(λśr) = 0,0089
Dla f=1-00Hz
λ={ 0,26 0,26 0,27 0,22 0,34}
λśr = 0,27
S(λśr) = 0,05
b) częstotliwość:
dla f=700hz Δ1/f = 0.00002 s
dla f=800hz Δ1/f = 0.0000156 s
dla f=1000hz Δ1/f = 0.000001 s
7.Obliczenie niepewności pomiarowych prędkości dźwięku metodą najmniejszych kwadratów:
Korzystając z wzorów:
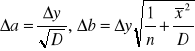
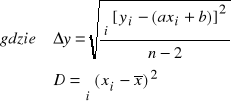
Δa =1
Więc : V = 305,1 ± 1 [m/s]
8. Porównuje liczbę stopni swobody z wielkością teoretyczna:
|
Wartość teoretyczna |
Wartość wyznaczona |
Współczynnik κ |
1,3 |
1,676 |
Liczba stopni swobody i |
6 |
3 |
Obliczona liczba stopni swobody w dla dwutlenku w węgla jest stanowczo za mały.W tym doświadczeniu trudno jest uzyskać dużą dokładność liczby stopni swobody, ponieważ sposób obliczania wymaga bardzo dokładnego wyznaczenia prędkości dźwięku w gazie. We wzorze na współczynnik ![]()
prędkość jest podnoszona do kwadratu, a następnie obliczony współczynnik jest wykorzystywany w zależności na liczbę stopni swobody, w której niewielkie zmiany ![]()
przekładają się na duże zmiany ![]()
.
WNIOSKI:
Pomiary zostały wykonane dla dźwięku o częstotliwości od 700 Hz do 1000 Hz. Okazało się, iż w miarę przechodzenia do wyższych częstotliwości zwiększała się ilość minimów.
Otrzymane w wyniku doświadczenia rezultaty odbiegają nieco od wartości teoretycznych.
Spowodowane jest to brakiem wystarczającej precyzyjności przyrządów pomiarowych a co za tym idzie niedokładnością pomiarów. Jednak wyniki uzyskane w doświadczeniu mieszczą się w dopuszczalnej granicy błędów.
0,2
0,25
0,3
0,35
0,4
0,45
0,5
0,55
0,0008
0,0009
0,001
0,0011
0,0012
0,0013
0,0014
0,0015
1/f [sek]
Długość fali [m]
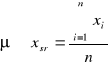
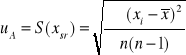
Wyszukiwarka
Podobne podstrony:
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
8 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
[10]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[8]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
cw 11- opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowaniemoje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
10 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[9]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Opracowanie11, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
11 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[5]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
8 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, Sprawozdan
Opracowanie6, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, la
Opracowanie05, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, l
[6]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
opracowanie cw 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
więcej podobnych podstron