Kontaktowa różnica potencjałów. Cechowanie termoogniwa. Pomiar temperatury wrzenia cieczy

Wstęp:

Kontaktowa różnica potencjałów na styku dwóch różnych metali jest wyni­kiem tzw. potencjału VOLTY. Już w 1797 r. YOLTA stwierdził, że przy zetknięciu dwóch różnych metali powstaje między nimi różnica potencjału. Uszeregował metale w ten sposób, że każdy poprzedni metal przy zetknięciu z dowolnym następnym elektryzuje się dodatnio. Szereg ten jest następujący: Al, Za, Sn, Cd, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd.

Wyjaśnienie kontaktowej różnicy potencjałów opiera się na mechanice kwantowej, a nie klasycznej. Według mechaniki kwantowej, każdy układ może znajdować się w ściśle określonych dla siebie stanach energetycznych. Mecha­nika klasyczna nie stawia układowi takich ograniczeń, zatem układ może przyjmować dowolne energie w granicach jakiegoś przedziału.

Poszczególnym orbitom (stanom energetycznym) elektronów w atomie odpowiadają określone wartości energii, rozumianej jako suma energii kinety­cznej i potencjalnej tych elektronów:

gdzie:

m − masa elektronu,

e − ładunek elektronu,

Z − liczba atomowa pierwiastka,

ε₀ − przenikalność elektryczna próżni,

h − stała Plancka,

n −główna liczba kwantowa.

Liczba elektronów na poszczególnych poziomach energetycznych jest określona przez zasadę Pauliego. Mówi ona, że w atomie na danym poziomie energetycznym (jeżeli nie jest zdegenerowany) nie może być dwóch elektronów o tych samych czterech liczbach kwantowych. Pierwsze trzy liczby kwantowe n, l, m opisują odpowiednio kształt, rozmiary i położenie orbity elektronu w prze­strzeni, czwarta liczba s — spin odnosi się do ruchu obrotowego elektronu wokół własnej osi. Widma energetyczne atomów jednego pierwiastka są iden­tyczne. Można by stąd wnioskować, że zbiór atomów jednego pierwiastka moż­na opisać takim samym modelem energetycznym, jak dla pojedynczego atomu. Takie założenie jest słuszne dla stanu gazowego, natomiast dla ciał stałych jest błędne. W ciałach stałych — kryształach atomy są tak blisko siebie, że następuje nakładanie się poziomów energetycznych elektronów walencyjnych, a to prowa­dzi do rozszczepienia pojedynczego poziomu energetycznego na tyle podpoziomów, ile jest atomów w danym krysztale.

W ujęciu kwantowym o rozmieszczeniu elektronów na poziomach decyduje zasada Pauliego. Funkcja opisująca ten rozkład elektronów w zależności od ich energii. E ma postać:

gdzie:

E_T — energia poziomu Fermiego w danej temperaturze.

Poziom Fermiego określa energię najwyższego z zajętych przez elektrony po­ziomu w temperaturze zera bezwzględnego. Z wyrażenia powyżej wynika, że dla:

1. E<E_T wykładnik potęgi jest bliski zeru, tzn. ƒ≈,1;

2. E = E_T otrzymuje się Ⴆ= 1/2;

3 E>E_T funkcja wykładnicza szybko rośnie, natomiast Ⴆ→0.

Energia poziomu Fermiego w temperaturze T jest określona wyrażeniem:

gdzie:

E_F — energia poziomu Fermiego w temperaturze T= 0 K jest określona wzorem:

gdzie:

m — masa elektronu,

n — liczba elektronów walencyjnych.

Aby wyjaśnić jak powstaje kontaktowa różnica potencjałów między dwoma me­talami weźmy pod uwagę dwa metale A i B, które nie stykają się ze sobą.

Na zewnątrz metali energia potencjalna elektronu jest równa zeru.

Z modelu na rysunku wynika, że elektrony w metalu A mają niższy potencjał, ale większą ener­gię, natomiast w metalu B jest odwrotnie potencjał mają większy, energię zaś mniejszą. Po złączeniu tych metali ze sobą elektrony zaczną przepływać z metalu o większej energii do metalu o mniejszej energii. Przepływ potrwa tak długo, aż wyrówna się energia całkowita elektronów w układzie. Warunkiem równowagi dynamicznej na sty­ku jest równość energii elektronów swobodnych w obu metalach - odpowiada to zrównaniu się poziomów Fermiego Metal oddający elektrony uzyskuje potencjał wyższy, przyjmujący zaś elektrony −potencjał niższy. W ten sposób wytworzyła się na styku metali różnica potencjałów (napięcie kontaktowe). Powstałej różnicy potencjałów towarzyszy pole elektryczne skierowane do metalu, który uzyskał mniejszy potencjał. Pole to hamuje dalszy przepływ elektronów.

Zestawienie pomiarów:

Termopara 1 − stal

Termopara 2 − miedz, aluminium

		Termopara 1				Termopara 2
	T [°C]	ε1 [mV]	ε2 [mV]	εśrednie	c	ε1 [mV]	ε2 [mV]	εśrednie	c
	25	1,2	1,2	1,2	0,05217	0,9	0,8	0,85	0,03696
	30	1,4	1,5	1,45	0,05179	1	1	1	0,03571
	35	1,7	1,7	1,7	0,05152	1,2	1,2	1,2	0,03636
	40	1,9	2,1	2	0,05263	1,4	1,4	1,4	0,03684
	45	2,1	2,3	2,2	0,05116	1,5	1,5	1,5	0,03488
	50	2,5	2,5	2,5	0,05208	1,7	1,7	1,7	0,03542
	55	2,6	2,7	2,65	0,05	1,8	1,8	1,8	0,03396
	60	3	2,9	2,95	0,05086	2	2	2	0,03448
	65	3,2	3,2	3,2	0,05079	2,2	2,1	2,15	0,03413
	70	3,5	3,4	3,45	0,05074	2,3	2,3	2,3	0,03382
	75	3,7	3,7	3,7	0,05068	2,5	2,5	2,5	0,03425
	80	4	4	4	0,05128	2,6	2,6	2,6	0,03333
	85	4,2	4,2	4,2	0,0506	2,8	2,8	2,8	0,03373
	90	4,5	4,5	4,5	0,05114	2,9	2,9	2,9	0,03295
	95	4,8	4,8	4,8	0,0516	3,1	3,1	3,1	0,03333
	100	5	5	5	0,05102	3,2	3,2	3,2	0,03265
Denaturat				4			2,6

Wartości wrzenia denaturatu odczytane z wykresu dla obu termopar wynoszą 80°C.

Obliczam temperaturę wrzenia denaturatu. Stosując następujący wzór po odpowiednich przekształceniach.

gdzie: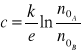
jest stałe

ε − jest średnią wartością siły termoelektromotoryczną obliczoną wcześniej.

T_a − temperatura odczytywana termometru

T_b = 2°C − temperatura lodu

Obliczam współczynnik c.

Wyniki obliczeń w tabelce po wyżej.

Średnie wartości współczynnika c dla termopary 1 wynosi c_śr = 0,05125

dla termopary 2 wynosi c_śr =0,03455

Temperaturę wrzenia denaturatu obliczamy ze wzoru:

gdzie: ε jest wartością odczytaną z miernika dla denaturatu dla termopary 1 ε = 4 ;

dla termopary 2 ε = 2,6

Dla termopary 1 T_a = 80 °C ; dla termopary 2 T_a =77 °C

Rachunek błędu:

Błąd dla wartości odczytywanych z przyrządów:

ΔT = 1°C

Δε = 0,1 mV

Błąd dla obliczania średniej wartości ε ze wzoru:

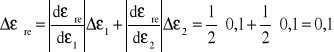
Błąd w obliczaniu współczynnika c.

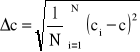
Dla termopary 1

Δc = 0,00063

Dla termopary 2

Δc = 0,00125

Błąd obliczenia temperatury wrzenia denaturatu.

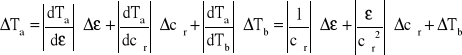
Dla termopary 1 ΔT_a = 3,9 °C ≈ 4 °C

Dla termopary 2 ΔT_a = 3,9 °C ≈ 4 °C

5

---