Nazwisko Frąc Imię Mariusz							Wydział ZiPT Grupa WT 3.1
Data wykonania 98.10.19.		Numer ćwiczenia E 3.2		Temat ćwiczenia : Wyznaczanie oporu elektrycznego metodą mostka Wheatstone'a.
Zaliczenie		Ocena		Data	Podpis

1. Część teoretyczna.

Metale charakteryzują się wysoką przewodnością elektryczną, dzięki przestrzeni utworzonej przez jony sieci krystalicznej, w której poruszają się swobodne elektrony, zwane elektronami przewodnictwa.

Jeżeli do końców metalowego przewodnika o długości l przyłożymy napięcie U to powstaje w nim pole elektryczne o natężeniu:

E=
.

Pole to powoduje, że chaotyczny ruch elektronów zamienia się w ruch uporządkowany, zachodzący w kierunku przeciwnym do kierunku wektora natężenia pola. W przewodniku płynie prąd elektryczny, a natężenie prądu jest równe sumarycznemu ładunkowi, przenoszonemu przez elektrony w jednostce czasu przez przekrój poprzeczny S przewodnika:

i = e⋅n₀⋅S⋅u

e - ładunek elektronu,

n₀ - liczba swobodnych elektronów w jednostce objętości metalu,

u - średnia prędkość ruchu uporządkowanego, którą oblicza się jako średnią arytmetyczną prędkości ruchu uporządkowanego na początku i na końcu drogi swobodnej.

Jeżeli u = e⋅λ/2mν ⋅
to i = e²⋅n₀⋅λ / 2mν ⋅
⋅U

Wprowadzając oznaczenie:

R = 2m⋅ν / e²⋅n₀⋅λ ⋅
,

otrzymujemy prawo Ohma w postaci:

i =
.

Wielkość R jest oporem elektrycznym, zwanym też rezystancją.

Jednostką oporu elektrycznego jest ohm:

1[Ω] =
.

Opór R jest wielkością charakteryzującą metal pod względem przewodzenia elektrycznego. Nie zależy on od napięcia oraz od natężenia przepływającego prądu, natomiast jest on związany z geometrycznymi rozmiarami przewodnika.

Ze względów praktycznych opór przewodnika wyraża się wzorem

R = ρ⋅
,

ρ - opór właściwy określony jako:

ρ = 2m⋅ν / e²⋅n₀⋅λ .

Odwrotnością oporu właściwego jest właściwa przewodność elektryczna, która wyraża się wzorem:

σ = e²⋅n₀⋅λ / 2m⋅ν.

Wysoka przewodność elektryczna metali, w porównaniu z innymi przewodnikami elektryczności, jest głównie związane z bardzo dużą ilością swobodnych ładunków elektrycznych.

2. Cel ćwiczenia:

Celem ćwiczenia było zmierzenie niewiadomego oporu Rx, przy pomocy mostka Wheatstone'a .

3. Opis ćwiczenia.

Najprostszym układem mostkowym, służącym do pomiaru oporu przewodników jest mostek Wheatstone'a, którego schemat ideowy przedstawiam poniżej.

Układ złożony jest z dwóch obwodów ( oczek ), zawierające elementy Ε, R_x, R₃ oraz Ε, R₁, R₂ dla których II prawo Kirchhoffa ma postać:

Ε = i₁⋅ ( R_x + R₃ ) oraz Ε = i₂⋅ ( R₁ + R₂ ).

Z powyższych równań można wyznaczyć natężenia prądów w obu oczkach:

i₁ = Ε / R_x + R₃ ; i₂ = Ε / R₁ + R₂.

Napięcie U między punktami C i D jest różnicą napięć występujących na końcach oporów R_x i R₁ , tak więc

U = i₁R_x - i₂R₁.

Napięcie U będzie równe zeru, jeżeli wartości oporów będą spełniały równanie:

R_xR₂ = R₁R₃,

zwane warunkiem zerowania lub warunkiem równowagi mostka. Wskaźnikiem stanu równowagi jest galwanometr włączony między punktami C i D, który wskaże natężenie prądu i_g = 0, jeżeli mostek będzie zrównoważony.

W naszym ćwiczeniu opór R₃ jest oporem dekadowym, natomiast R₁ i R₂ jest drutem oporowym o długości l, przekroju poprzecznym S i oporze właściwym ρ. Ustawiając suwak w takie położenie C, przy którym prąd przez galwanometr nie płynie, oraz oznaczając przez a długość odcinka AC, opory R₁ i R₂ są określone następująco:

i
.

Natomiast szukany opór R_x obliczamy ze wzoru:

.

Metoda mostkowa jest metodą porównawczą. Dokładność pomiaru zależy głównie od właściwego doboru oporów R₁, R₂, i R₃. Najlepsze wyniki osiąga się przy wartościach oporów zbliżonych do R_x.

4. Opracowanie wyników pomiaru.

Nr oporu Rx	l [ m ]	a [ m ]	R3 [ Ω ]	Rx [ Ω ]	Rx [ Ω ]
R1	1	0,45	30	24,5	21,9
				0,5		25	25
				0,55		20	21,2
		R8	1	0,45		250	204,5	207,4
				0,5		210	210
				0,55		170	207,7
		R11	1	0,45		600	490,9	479,3
				0,5		500	500
				0,55		410	501,1

Błąd względny

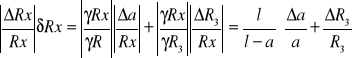
δ_R1= 0,0424 ⋅ 100% = 4,24%

δ_R8= 0,0226 ⋅ 100% = 2,26%

δ_R11= 0,0211⋅ 100% = 2,11%

błąd bezwzględny pomiaru związany z klasą przyrządu pomiarowego

Δa = Δa^' + Δa^'' = 0,001 + 0,004 = 0,005

Δa^'= klasa x zakres / 100

Δa^''= zakres/ liczba działek

Błąd ustawienia oporu na rezystorze dekadowym

ΔR₃=ΔR₃₁ + ΔR₃₂ +ΔR₃₃

błędy dla poszczególnych dekad

ΔR₃₁= klasa% x zakresΩ / 100%

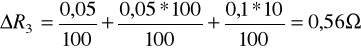
błąd bezwzględny

ΔRx = Rx⋅δ_RX [Ω]

Rx= Rxśr +/- δRx [Ω]

ΔR₁= 0,92 [Ω] R₁= 21,9
[Ω]

ΔR₈= 4,68 [Ω] R₈= 207,7
[Ω]

ΔR₁₁= 10,49 [Ω] R₁₁= 497,3
[Ω]

Wnioski:

Otrzymany doświadczalnie wynik pomiaru rezystancji został obarczony małym błędem, możemy przyjąć, że pomiary zostały przeprowadzone prawidłowo. Niewielki błąd wynika z niedokładności przyrządów pomiarowych i błędów przy odczycie.

R3

D

Rx

R1

R2

A

C

E

B

---