Z1 13, SPRAWOZDANIA czyjeś

Pobierz cały dokument z1.13.sprawozdania.czyjes.doc Rozmiar 99 KB

Fragment dokumentu:

WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH

Seminarium semestr zimowy 2000/2001

Prowadzący: dr inż. Wojciech Krzysztofik

Michał Zubrzycki (95466)

Zadanie Z1/13

1. Treść zadania

Korzystając z twierdzenia Parsevala i własności symetrii transformaty Fouriera sprawdzić ortogonalność dwóch funkcji próbkujących f₁(t) i f₂(t) w przedziale nieskończonym -∞<t<∞.

, tw. Parsevala: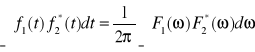
.

,
,

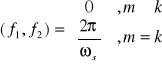
2. Wprowadzenie teoretyczne

Dwie funkcje są ortogonalne, jeśli jeden sygnał f₁(t) nie zawiera żadnej składowej drugiego sygnału f₂(t). Czyli dwie funkcje f₁(t) i f₂(t) są ortogonalne w przedziale (t₁, t₂), jeżeli:

.

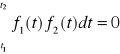
Dla układu funkcji f₁(t), f₂(t), ...,f_n(t) wzajemnie ortogonalnych mamy:

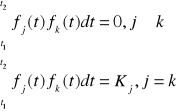
3. Rozwiązanie

Aby sprawdzić, czy funkcje są ortogonalne, należy policzyć całkę:

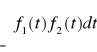
i sprawdzić, czy dla k≠m wynosi 0, a dla k=m wynosi
(zgodnie z treścią zadania).

Zamiast liczyć tę całkę, można skorzystać z twierdzenia Parsevala. Do tego potrzebne mi są transformaty fouriera funkcji f₁(t) i f₂(t).

Aby policzyć te transformaty korzystam z twierdzenia o symetrii tranformaty fouriera:

Wiedząc, że transformatą impulsu prostokątnego jest funkcja samplująca:

(łatwo to wyprowadzić metodą pochodnych), można znaleźć transformatę funkcji samplującej korzystając z twierdzenia o symetrii:

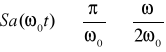
korzystając z twierdzenia o przesunięciu w dziedzinie czasu:

i wiedząc, że
znajduję transformaty zadanych funkcji:

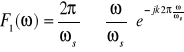
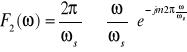
teraz korzystając z twierdzenia Parsevala można obliczyć całkę iloczynu f₁ i f₂ dla k=m:

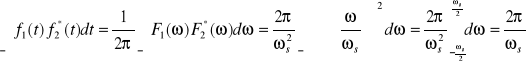
czyli dla k=m otrzymuję:

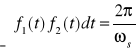
Jest to wynik odpowiadający funkcjom ortogonalnym.

Teraz korzystając z twierdzenia Parsevala obliczam całkę iloczynu f₁ i f₂ dla k≠m:

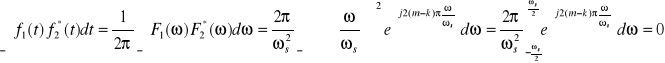
czyli dla k≠m otrzymuję:

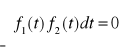
Czyli funkcje f₁(t) i f₂(t) są ortogonalne.

3

2π/ω₀

ω

TSa

ωT

2

T

4π/T

0

4π/T

Pobierz cały dokument z1.13.sprawozdania.czyjes.doc rozmiar 99 KB