POMIAR PRZYŚPIESZENIA ZIEMKSIEGO PRZY POMOCY WAHADŁA MATETATYCZNEGO

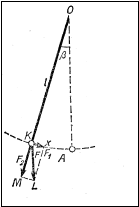
1.Teoria Wahadła Matematycznego

WAHADŁO- bryła sztywna wykonująca drgania wokół osi (zwykle poziomej) nieprzechodzącej przez środek ciężkości bryły; w zależności od konkretnych rozwiązań i zastosowań rozróżnia się: wahadło rewersyjne, wahadło balistyczne, wahadło kompensacyjne, wahadło torsyjne, wahadło zegarowe.
WAHADŁO MATEMATYCZNE, punkt materialny zawieszony na nieważkiej i nierozciągliwej nici (o dł. d), której drugi koniec jest unieruchomiony; dla małych wychyleń okres drgań w. mat. prostego (punkt porusza się w płaszczyźnie pionowej po łuku okręgu) jest w przybliżeniu stały (izochronizm) i równy.

2. Przyrządy Pomiarowe

Na metalowym pręcie umieszczona jest lekka płytka, która w zależności od ustawienia względem płaszczyzny ruchu wahadła powoduje większy lub bardzo mały opór powietrza. Prócz tego możemy zmienić moment bezwładności. Wahadła, umieszczając na pręcie dodatkową masę m. Do tego wykorzystamy: sznurek, przyrząd do mierżenia długości, stojak, obciążnik.

3.Opis Doświadczenia

1) Zawiesić wahadło na stojaku.

2) Mierzymy długość sznurka, co będzie nam potrzebne do obliczeń.

3) Wprawiamy wahadło w ruch, i powtarzamy czynności z punktu 2 (10-razy).

4) Zapisujemy przebieg doświadczenia w tabeli (zamieszczonej niżej).

5) Obliczamy średnią długość i okres wahań.

6) Przekształcamy wzór tak, aby obliczyć wartość „przyśpieszenia ziemskiego” ***.

7) Przedstawimy Rachunek błędu.

8) I podsumowujemy nasze zaobserwowania.

4.Tabela Pomiarowa

LP.	Długość	Czas 10 Wahnięć		Okres Wahań
1.	1,04cm	20,24	2,024
2.	1,04cm	18,01	1,81
3.	1,04cm	20,37	2,037
4.	1,04cm	19,26	1,926
5.	1,04cm	20,67	2,067
6.	1,04cm	20,14	2,014
7.	1,04cm	20,25	2,025
Średnia 1,04 cm			Średni okres wahań 1,986

5.Obliczenia

W położeniu wychylonym na punkt ten działa siła poruszająca:

gdzie ciężar wahadła:

Łącząc powyższe równania i podstawiając:

gdzie s jest wychyleniem punktu w stosunku do położenia równowagi otrzymamy:

Ponieważ m, l, g są dla określonego wahadła wielkościami stałymi, a więc siła poruszająca F jest wprost proporcjonalna do wielkości wychylenia s. Wynika stąd, że ruch wahadłowy jest dla małych wychyleń ruchem harmonicznym.

Przyspieszenie ruchu harmonicznego wyrażone jest równaniem:

stąd siła poruszająca:

Porównując tę wartość z uprzednio wyprowadzonym równaniem:

otrzymujemy:

a stąd

Z powyższego równania wynika, że okres wahań wahadła matematycznego nie zależy od amplitudy i masy wahadła, natomiast zależy od jego długości i wartości działającego w danym miejscu przyspieszenia ziemskiego.

Patrząc na ten wzór od razu widzimy, że:

Okres wahań nie zależy od kąta wychylenia wahadła.

Nie zależy on również od masy wahadła.

Jest proporcjonalny do pierwiastka kwadratowego z długości wahadła

Jest odwrotnie proporcjonalny do pierwiastka kwadratowego z przyspieszenia ziemskiego

OBLICZENIA:

6.Rachunek Błędu

1)Największy wpływ na dokładność wyniku ma pomiar okresu T.

2)Błędem obarczony jest również pomiar długości nitki l.

3)Drgania kulki wahadła powinny odbywać się w jednej płaszczyźnie.

4)Wzór na okres drgań wahadła matematycznego jest słuszny jedynie w przypadku, gdy kulka nie jest narażona na żadne opory ruchu.

7.Wnioski

Dzięki temu doświadczeniu możemy zaobserwować jak w prosty sposób możemy obliczyć przybliżona wartość przyspieszenia ziemskiego, i w jakie jest działanie wahadła matematycznego.

*** PRZYSPIESZENIE ZIEMSKIE (g), przyspieszenie ciał swobodnie spadających na Ziemię (przy pominięciu oporu powietrza); wartość zależy od szerokości geograficznej, miejsca pomiaru, lokalnego rozkładu mas wewnątrz Ziemi. Za normalną wartość przyjęto: gn= 9,80665 m/s2. p.z. na szerokości geograficznej 45° i poziomie morza.

---