FUNKCJA KWADRATOWA - PRACA KLASOWA GR A

1. Zapisz wzór funkcji, która powstanie w wyniku przesunięcia funkcji
   

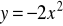
1. o 2 jednostki w prawo

2. o 1 jednostkę w górę i 5 jednostek w lewo.

2. Rozwiąż nierówności:

a)

b)

c)

d)

3. Narysuj wykres funkcji
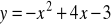
   i podaj jej własności. Zapisz wzór tej funkcji w postaci iloczynowej.

4. Prostokąt ma boki długości 10 cm i 6 cm. Dłuższy bok skracamy o x, natomiast krótszy wydłużamy o x. Dla jakiej wartości x pole nowego prostokąta jest największe?

5*. Suma cyfr pewnej liczby dwucyfrowej wynosi 5. Iloczyn tej liczby i liczby o tym samych, ale

przestawionych cyfrach wynosi 574. Zapisz treść zadania w postaci układu równań. Znajdź tę

liczbę.

FUNKCJA KWADRATOWA - PRACA KLASOWA GR B

1. Narysuj wykres funkcji
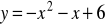
   i podaj jej własności. Zapisz wzór tej funkcji w postaci kanonicznej.

2. Zapisz wzór funkcji, która powstanie w wyniku przesunięcia funkcji
   

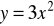
1. o 1 jednostkę w dół i 3 jednostki w prawo

2. o 2 jednostki w lewo.

3. Rozwiąż nierówności:

a)

b)

c)

d)

4. Dla jakiego argumentu x różnica
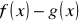
   jest najmniejsza, jeśli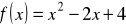
   i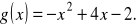
   

5*. Suma cyfr pewnej liczby dwucyfrowej wynosi 5. Iloczyn tej liczby i liczby o tym samych, ale

przestawionych cyfrach wynosi 736. Zapisz treść zadania w postaci układu równań. Znajdź tę

liczbę.

Rozwiązywanie nierówności kwadratowych - kartkówka

GR A

Rozwiąż nierówność

a)

b)

c)

d)

e)

GR B

Rozwiąż nierówność

a)

b)

c)

d)

e)

Funkcja kwadratowa - wykres i własności - kartkówka

GR A

Naszkicuj wykresy funkcji:

a)

b)

c)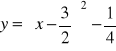

i określ własności jednej z nich.

GR B

Naszkicuj wykresy funkcji:

a)

b)

c)

i określ własności jednej z nich.

GR C

Naszkicuj wykresy funkcji:

a)

b)

c)

i określ własności jednej z nich.

GR D

Naszkicuj wykresy funkcji:

a)

b)

c)

i określ własności jednej z nich.

Rozwiązywanie równań kwadratowych - kartkówka

GR A

Rozwiąż równania (postaraj się wybrać jak najprostszą metodę):

1. 30 - 13x + x² = 0

2. 5(3 - x)² + 15(3 + 2x) = 0

3. (2x - 5)² = 4

4. -3x² + 6x - 3 = 0

5. 2x² + 4x = 0

GR B

Rozwiąż równania (postaraj się wybrać jak najprostszą metodę):

1. 50x - 8x² = 0

2. (3x + 1)² = 9

3. -1 - 2x + 3x² = 0

4. -2x² + 4x - 2 = 0

5. 3(x - 3)² - 6(2 - 3x) = 0

opracowanie: mgr Joanna Januszewska

---