32.b) Obliczyć objętość obszaru ograniczonego powierzchniami:

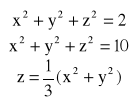
Zamieniłem zmienne z i x w ostatnim równaniu, co nie zmienia nijak objętości, bo ta paraboloida (jak sądzę) pozostaje paraboloidą tyle, że wzdłuż innej osi. Reszta to sfery, więc ich symetria pozwala na zrealizowanie takiej zamiany bez zmiany wyniku...

W pierwszym rówaniu L=±2 , dla -2 delta będzie ujemna więc ta druga część nie przetnie się ze sferami.

Przechodzę na wsp. cylindryczne i sprawdzam równość zetów:

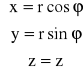
J=r

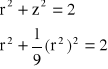
Podstawiam r²=t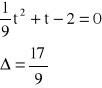

czyli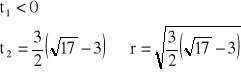

Analogicznie postępuję z równaniami 1 i 3. Otrzymuję:

Całość dzielę na dwie objętości:

I) II)

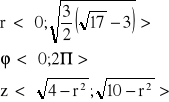
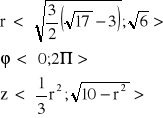
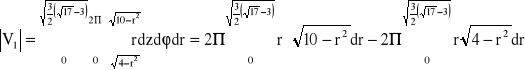
Wiedząc, że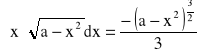
otrzymuję:

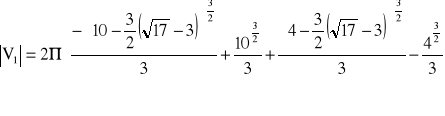
Objętość druga natomiast:

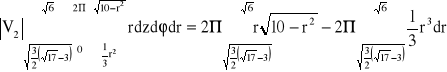
Podobnie jak poprzednio:

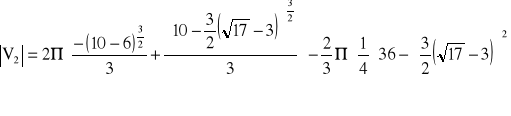
Po prostych przekształceniach arytmetycznych otrzymuje się wynik:

---