Każda macierz kwadratowa, której wyznacznik jest różny od 0 nazywamy macierzą nieosobliwą. Można udowodnić, że:

Dla każdej macierzy kwadratowej A istnieje co najwyżej jedna macierz B taka że

B*A=A*B=I (1)

I - macierz jednostkowa, tzn. I=[a_ij], i,j=1,2…..n, przy czym a_ij=1 gdy i=j oraz aij=0gdy i≠j

Jeżeli dla danej macierzy kwadratowej A istnieje macierz B spełniająca równość (1), to macierz B nazywamy macierzą odwrotną i oznaczamy symbolem A^-1.

Tw.2. Dana macierz kwadr. posiada macierz odwrotną jest nieosobliwa.

Jeżeli A jest macierzą nieosobliwą to macierz odwrotna do niej jest dana wzorem:

A^-1 = 1/detA [(-1)^i+j*M_ij]^T i,j = 1,2…n

gdzie M_ij jest minorem macierzy A tzn. wyznacznikiem macierzy stopnia (n-1) otrzymanej z mac. A przez skreślenie i-tego wiersza dla j-tej kolumny.

Jeśli A jest macierzą stopnia n a I jest macierzą jednostkową stopnia n to A*I=I*A=A

3. Rozwiązywanie układów równań algebraicznych liniowych.

Dany jest układ (u) o n niewiadomych:

a₁₁x₁+ a₁₂x₂+…+ a_1nx_n = b₁

a₂₁x₁+ a₂₂x₂+…+ a_2nx_n = b₂

…

a_n1x₁+ a_n2x₂+…+ a_nnx_n = b_n

gdzie a_jk, b_j
R ; j,k = 1,2...n

Macierz

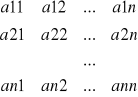
Nazywamy macierzą układu (u).

Układ (u) nazywamy układem Cramera gdy macierz A układu jest nieosobliwa, czyli detA≠0

Niech x=[x1,x2,…xn]^T ; b=[b1,b2,…bn]^T

Wtedy układ możemy zapisać w postaci macierzowej:

*

=

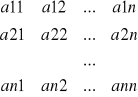
Lub A*x=b

Każdy układ liczb x1, x2, … xn spełniający układ (u) nazywamy rozwiązaniem układu.

Tw.1. (Cramer) Każdy układ Cramera postaci (u) ma dokładnie 1 rozwiązanie, dane wzorem:

x_k = detA_k/detA ; k=1,2….n

gdzie A_k jest macierzą powstałą z macierzy A układu (u) przez zastąpienie k-tej kolumny przez kolumnę wyrazów wolnych b1, b2, …bn.

Rozwiązanie układu (u) możemy przy pomocy macierzy zapisać następująco:

x=A^-1*b

gdyż mnożąc lewostronnie równanie A*x=b przez A^-1 otrzymujemy x=A^-1*b.

Uwaga: jeśli układ równań liniowych (u) jest układem jednorodnym tzn b1=b2=…=0 oraz (u) jest układem Cramera to istnieje tylko rozwiązanie x1=x2=…=xn tego układu.

4. Rozwiązywanie zagadnienia własnego macierzy kwadratowej.

Def. grupy: niepusty zbiór G z funkcją

:G x G -> G

Zwaną działaniem w G oraz wyróżnionym elementem e, zwanym elementem neutralnym, nazywamy grupą, jeżeli:

a)
- lączność

b)

c)
(a^-1 - element odwrotny do a)

Jeżeli ponadto

d)
- przemienność

to grupę G nazywamy przemienną lub abelową.

Grupa jest więc przyporządkowana trójką (G,
, e)

Def. Dany jest zbiór niepusty K, w którym wyróżniono elementy 0,1
K, 0≠1 oraz zostały określone działania:

+: K x K -> K

: K x K -> K

Takie że:

1. (K, +, 0) jest grupą abelową

2. (K\{0},
   ,1) jest grupą abelową

3. 
   a*(b+c) = a*b + a*c

Wówczas zbiór (K, +,
, 0, 1) nazywamy ciałem.

Przykłady: Zbiory (R, +,
, 0, 1), (C, +,
, 0, 1) - C-zb.l. zespolonych; R- rzeczywistych

są ciałami.

Uwaga: w dalszym ciągu symbol K oznaczać będzie którykolwiek element zbioru {R, C}

Def. Niech K będzie ciałem (K=R lub K=C), a (X, +,
) grupą abelową. Elementy zbioru X będziemy nazywać wektorem, a elementy ciała K skalarami lub liczbami.

Element O
X to tzw. wektor zerowy. Każdej liczbie α
K oraz każdemu wektorowi x
X przyporządkowujemy jednoznacznie wektor α *x
X, przy czym dla dowolnych liczb α,β
K; x,y
X

1. α(β*x)= (α*β)x

2. 1*x=x

3. α (x+y)= α*x+ α*y

Wtedy parę (X, K) nazywamy przestrzenią liniową lub wektorową. Jeżeli K=R, to rzeczywistą przestrzenią liniową (X, R)

Jeżeli K =C to mamy zespoloną przestrzeń liniową (X, C)

---