Zadanie proste kinematyki manipulatora

Niech

A_i =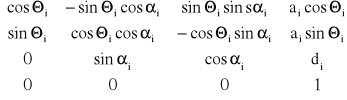

Obieramy zmienne kinematyczne, gdy para kinematyczna jest :

1. obrotowa - zmienną kinematyczną jest _i

2. przesuwna - zmienną kinematyczną jest _i

Przykładowo ( dla manipulatora stanfordzkiego )

I	i	di	ai	i
1	var	d1	a1	1
2	var	d2	a2	2
3	3	var	a3	3
4	var	d4	a4	4
5	var	d5	a5	5
6	var	d6	a6	6

Macierze dla manipulatora stanfordzkiego

A₁(₁), A₂(₂), A₃(d₃), A₄(₄), A₅(₅), A₆(₆)

Dla par kinematycznych klasy piątej

q_i = _i dla pary obrotowej

q_i = d_i dla pary translacyjnej

Czyli

dla N stopni swobody manipulatora.

Przykładowa macierz wyrażająca pozycję i orientację drugiego układu względem bazowego :

T₂ = A₁(q₁) A₂(q₂)

Znając q(t₀) można określić pozycję i orientację manipulatora w chwili t₀.

Gdy dany jest wektor q na jego podstawie znajdujemy wektor położenia manipulatora

q [ x_CS y_CS z_CS a b c ]^T

gdzie

x_CS

y_CS współrzędne początku lokalnego układu współrzędnych ( w układzie globalnym )

z_CS

a

b kosinusy kierunkowe, kąty Eulera, dwa kąty i oś

c

I A₁

A₂

T

A₁ A₂ A₃ A_N-1 A_N

I T_N

---