Scenariusz lekcji

klasa II Technikum Informatycznego

• Temat lekcji: Ciąg geometryczny -zadania.

Czas trwania 90 min

• Cele lekcji

1. Wiadomości:

Uczeń zna:

• pojęcia: ciąg, wyrazy ciągu

• pojęcia: ciąg skończony, ciąg nieskończony

• pojęcie ciągu liczbowego

• pojęcia: wzór ogólny ciągu

• pojęcia: ciąg geometryczny, iloraz ciągu geometrycznego

• wzór ogólny ciągu geometrycznego

1. Umiejętności:

Uczeń potrafi::

• zapisywać dowolne wyrazy ciągów na podstawie ich wzorów ogólnych

• obliczać iloraz i kolejne wyrazy danego ciągu geometrycznego

• obliczać dowolne wyrazy ciągu geometrycznego, gdy dane są jeden wyraz i iloraz ciągu lub dwa dowolne wyrazy tego ciągu

• podawać przykłady ciągów geometrycznych spełniających określone warunki

• sprawdzać, czy dana liczba jest wyrazem danego ciągu geometrycznego

• rozwiązywać zadania dotyczące ciągu geometrycznego

• obliczać sumę ciągu geometrycznego

• zapisuje wzór ogólny i rekurencyjny ciągu

1. Cele wychowawcze:

• pobudzanie aktywności i inicjatywy

• wpajanie nawyków argumentowania, posługiwania się językiem matematycznym

• budowanie u ucznia postawy zadowolenia z siebie, kształtowanie postawy gotowości niesienia pomocy innym

• Metody nauczania

• pogadanka

• omówienie sposobu rozwiązania

• praca uczniów przy tablicy

• pokaz

• prezentacja rozwiązania zadań

• ćwiczeniowe

• Środki dydaktyczne

• Podręczniki

• Tablica

• Zestawy z zadaniami

• Zasady nauczania

• zasada świadomości i aktywności uczniów

• stopniowania trudności

• zespołowości

• Przebieg lekcji

• czynności organizacyjne:

• realizacja tematu

• podanie tematu lekcji

• przypomnienie podstawowych informacji dotyczących ciągów

• co to jest ciąg

• kiedy ciąg jest rosnący, a kiedy malejący

• ciągi skończone i nieskończone

• podanie kilku przykładów ciągów geometrycznych

• wspólne zaobserwowanie pewnych zależności występujących w ciągach geometrycznych

• wprowadzenie pojęcia: iloraz ciągu, wyraz ciągu, wzór ogólny i rekurencyjny ciągu

• podanie definicji ciągu arytmetycznego

Zad.1

Jaka zależność zachodzi pomię­dzy wyrazami ciągów?:

(a_n)=(1,2,4,8,16,...)

(b_n)=(-81, 27, -9, 3,...)

Rozwiązanie:

• wyraz pierwszy a₁=1, iloraz wyra­zu następującego i poprzedzającego jest sta­ły i wynosi 2:

a₄ : a₃ = a₃ : a₂ = a₂ :a₁ = 2,

• wyraz pierwszy a₁ =-81, iloraz wy­­ra­zu następującego i poprzedza­ją­cego jest stały i wynosi 1/3:

a₄ : a₃ = a₃ : a₂ = a₂ :a₁ = 1/3.

Def.1.Ciągiem geometrycznym nazywa­­­my ciąg liczbowy, w którym każdy wyraz oprócz pierwszego jest iloczynem wyrazu poprzedzającego przez stałą liczbę q0 zwaną ilorazem ciągu lub postępem geometrycznym.

b₁

b₂= b₁^.q

b₃= b₂^.q = b₁^.q^.q = b₁^.q²

b₄= b₃^.q = b₂^.q^.q = b₁^.q³

...

b_n= b_n-1^.q =... = b₁^.q^n-1

Wniosek1:

b_n = b₁^.q^n-1







Wniosek2:

Stosunek dowolnego wyrazu ciągu do wyrazu poprzedzającego jest stały i wynosi q.

Zad.2.

W ciągu geometrycznym dane są:

b₁=2 q =3. Oblicz: b₂, b₃, b₄, b₅, b₇, b₉, b_n,

Zad.3.

Dane: a) b₁=1 q =-2

b) b₁=-3 q = ½

Oblicz: b₂, b₃, b₇, b₉, b_k-3, b_2k+1,

Zad.4.

Spośród czterech liczb b₁, q, b_n, n dane są trzy. Oblicz niewiadomą:

• b₁=1/2, q=2/3, n=7,

• b₁=-3/2, q=1/3, b_n=-1/54

• q=5/3, n=5, b_n=25/9

• q=-1/4, n=5, b_n=-1/32

Wniosek:

Suma n początkowych wyrazów ciągu geometrycznego wyraża się wzorem:




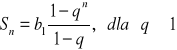
Wniosek:

Suma n początkowych wyrazów ciągu geometrycznego wyraża się wzorem:




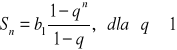
Pokazanie uczniom niebezpieczeństwa różnego rodzaju zakładów i łańcuszków szczęścia opartych na ciągu geometrycznym.

Zad.1

a) b₁ = -3, r = 4 Oblicz S₁₀ ,

b) b₁ = 0,5 , r = -1/4 Oblicz S_20.

Zad.2

Spośród liczb: b_1, q, n, b_n , S_n, oblicz brakujące:

a) q = 1/2, n= 10, S_n = 4 -1/2⁸ , b₁= ?

b) q = 3, n = 5, S_n = 121, n=?

c) b₁=20, q = -2, S_n = 860, n=?

d) b₁= -5, q = 0.1, n = 20, S_n =?

Zad.3

W ciągu geometrycznym zachodzą równości: b₁+ b₅ = 17 i b₂+ b₆ = -34. Ile wyrazów początkowych należy zsumować, aby otrzymać 43?

Zad.4

Pewien ciąg ma parzystą liczbę wyrazów, których suma jest trzy razy większa od sumy wyrazów o numerach nieparzystych. Wyznacz iloraz tego ciągu.

Zad.5

Wykaż, że jeżeli S_n , S_2n , S_3n oznaczają odpowiednio sumę n, 2n, 3n początkowych wyrazów ciągu geometrycznego (b_n), to S_n ( S_3n - S_2n)= ( S_2n - S_n)².

Zad.6

Suma 3n początkowych wyrazów rosnącego ciągu geometrycznego jest rów­na 14, a suma 2n początkowych wyrazów ciągu wynosi 6. Oblicz sumę n początko­wych wyrazów tego ciągu.

• ocena pracy uczniów

• zadanie pracy domowej

Zad.1

Cztery liczby rzeczywiste tworzą ciąg geometryczny, w którym suma wyrazów skrajnych wynosi -21, a suma wyrazów pozostałych jest równa 6. Znajdź te liczby.

Zad.2

Trzy liczby, których suma jest równa 7 tworzą ciąg geometryczny malejący. Największa z tych liczb jest o 100/3 % większa od sumy dwóch pozostałych.

Znajdź te liczby.

Zad.3

Podaj przykład ciągu rosnącego,

oraz malejącego. Podaj znak a₁ i q.

Zad.4

Czy ciąg (64,16,8,2,1,-3,-7)

Jest ciągiem geometrycznym?

Odpowiedź uzasadnij.

Zad.5

Dane: b₁=-3/2, n=4, b_n=375/16.

Oblicz q.

• podsumowanie pracy

Scenariusz lekcji

Matematyka klasa II Technikum opracował Robert Kłoczko 4

---