AGH EAIiE							Paweł Straszak
Laboratorium TEORII OBWODÓW
^rok akademicki 2001/2002	^rok studiów II		^semestr III	^Grupa 8	^Zespół 1
Temat : Stany nieustalone w obwodach elektrycznych.
^data wykonania 14.01.2002		^data zaliczenia 21.01.2002				^ocena

1. Dwójnik RL

Schemat obwodu:

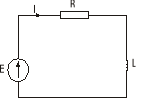
Parametry:

R=1kΩ

L=1H

U_m=5V

F=100Hz

E-fala prostokątna

Z wykresu odczytujemy wartość U_r do obliczenia wartości prądu I_r z zależności I_r=U_r/R

Ponieważ U_r=3,75V to I_r=0,00375A

Następnie obliczamy stałą τ z zależności τ=L\R. Dla naszego obwodu τ=1ms

2. Dwójnik RC

Schemat:

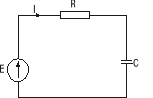
Parametry

R=3kΩ

C=0,4 μF

U_m=5V

f=100Hz

E-fala prostokątna

Z wykresu odczytujemy wartość U_r do obliczenia wartości prądu I_r z zależności I_r=U_r/R

Ponieważ U_r=9,5V to I_r=0,0032A

Następnie obliczamy stałą τ z zależności τ=R*C. Dla naszego obwodu τ=1,2ms

3. Dwójnik RLC

Schemat

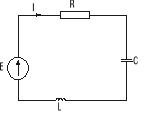
Dla tego obwodu możemy mieć trzy różne przypadki które opisujemy poniżej. Schemat w każdym z przypadków jest dokładnie taki sam a różnica polega jedynie na innych wartościach elementów R,L,C i na ilości rozwiązań równania charakterystycznego

1. Dwójnik RLC (przebieg aperiodyczny Δ>0)

Parametry:

R=4kΩ

L=1H

C=0,3μF

U_m=5V

f=100Hz

E-fala prostokątna

Delta jest większa od 0 więc jest to przebieg aperiodyczny.

Obliczamy pierwiastki równania charakterystycznego:

s₁ = - α + β

s₂ = - α - β gdzie: α = R / 2L

Dla naszych wartości elementów α = 2000, β = 408,2

Z kolei pierwiastki równania charakterystycznego wynoszą s₁=-1591,8 s₂=-2408,2

Z wykresu odczytujemy wartość czasu t po jakim zostanie osiągnięte maksimum U_RMAX.

U_RMAX=7,125V t=0,64 ms

Te dwei wielkości możemy również wyznaczyć korzystając ze wzorów:

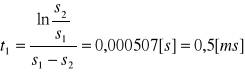
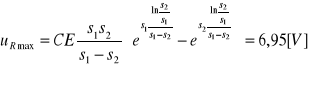
2. Dwójnik RLC (przebieg aperiodyczny krytyczny)

Parametry:

R=3kΩ

L=0,2H

C=0,11μF

f=100Hz

U_m=5V

E-fala prostokątna

Ponieważ delta
jest mniejsza od zera to jest to przebieg aperiodyczny krytyczny. Z wykresu odczytujemy maksymalną wartość napięcia na rezystorze, która wynosi U_RMAX=7,4V, a także czas, po którym to napięcie zostało osiągnięte t=0,128ms

3. Dwójnik RLC (przebieg oscylacyjny)

Parametry:

L=1H

R=2kΩ

C=0,02 μF

f=100Hz

U_m=5V

E-fala prostokątna

Dla tego przypadku delta

Z tego otrzymujemy, że α = 1000 β= 3500

Odczytujemy z wykresu wartości dwóch pierwszych maksimów, a także wartość okresu T:

T=3,93ms

A₁=2,25V

A₂=-1,25V

Powyższe wyniki możemy sprawdzić z wartościami teoretycznymi obliczonymi z wzorów:

T=2Π/β=0,38s

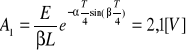
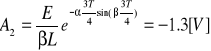
4. Wnioski

W punkcie pierwszym podłączyliśmy napięcie zmienne o przebiegu prostokątnym do obwodu RL. Jak widać na wykresie 1 napięcie powoli ustala się na odbiorniku. Jest to związane z elementem indukcyjnym L, który gromadzi energię elektromagnetyczną. Dlatego obserwujemy powolny wzrost napięcia na elemencie R.

W punkcie drugim badaliśmy odbiornik typu RC. Element C również gromadzi energię elektromagnetyczną. Na wykresie nr 2 obserwujemy spadek napięcia na elemencie R (aż do 0), gdyż kondensator stopniowo ładuje się i w granicznym przypadku (t zmierza do nieskończoności) stanowi dla obwodu przerwę.

Dla obwodów RLC mamy połączenie obydwu odbiorników. Dla wykresu 3 początkowo napięcie na odbiorniku R rośnie. Związane jest to z obecnością elementu L w obwodzie. Ale po osiągnięciu maksimum wartość napięcia na elemencie R maleje do zera tak jak to było w obwodzie RC. Element C stanowi przerwę w obwodzie, a co za tym idzie nie płynie w obwodzie prąd, więc napięcie maleje do zera. Podobną sytuację możemy zauważyć na wykresie 4.

---