1. Model matematyczny drgającego układu (dla dwóch stopni swobody) ma postać :
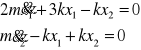
(m i k stałe dodatnie)
Wyznacz i narysuj postacie drgań własnych tego układu. Sprawdź bezpośrednim rachunkiem M- i K-ortogonalność postaci własnych.
2. Dla układu przedstawionego na rysunku wyznacz częstości i postaci drgań własnych. Przyjąć m = 1kg, k = 100 N/m
3. Jednorodny walec o promieniu R i masie M porusza się bez poślizgu między dwoma listwami. Jego ruch jest wynikiem poruszania się listew wzdłuż poziomych prostych x1 i x2. Listwy o masach m1 i m2 zamocowane są do sprężyn liniowych.
Napisz równania ruchu układu
Wyznacz częstości i postaci drgań układu
przyjmując: m1 = m2 = m, M = 8m, k1 = k,
k2 = 2k, k3 = 2k, k = k4 = 1000N/m, m = 1kg
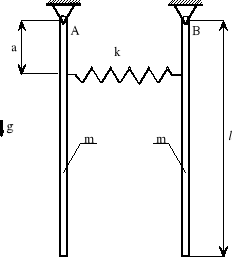
4. Dwa jednorodne pręty podwieszone jak na rys. połączone są sprężyną liniową o sztywności k. Wyznacz częstości i postaci drgań własnych układu. Długość swobodna sprężyny równa jest odległości AB.
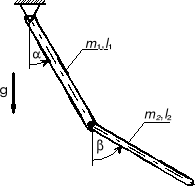
5. Dane jest wahadło fizyczne podwójne składające się z dwóch jednorodnych prętów o znanych masach i długościach. Napisz równanie charakterystyczne małych drgań tego układu
Wyszukiwarka
Podobne podstrony:
Zadania 01, MEiL, [NK 311] Drgania, Zadania treningowe
03 Równania kanoniczne, MEiL, [NK 336A] Mechanika analityczna, Zadania domowe
04 Teoria sterowania, MEiL, [NK 336A] Mechanika analityczna, Zadania domowe
01 Elementy rachunku wariacyjnego, MEiL, [NK 336A] Mechanika analityczna, Zadania domowe
Zadania nr 2, MEiL, Rok II, Drgania
02 Więzy, MEiL, [NK 336A] Mechanika analityczna, Zadania domowe
Zadania treningowe do ćwiczeń rachunkowych z chemii - kolokwium III, Studia, Moje, Chemia
3 kolo zadania treningowe przed kolokwium 2
Zadania treningowe MOMP B
Zadania treningowe MOMP A
MES1 zadania treningowe do kolokwium I
zadania treningowe kol2, Statystyka
MES1 zadania treningowe do kolokwium II
zadania treningowe
Zadania treningowe 2
MES1 zadania treningowe do kolokwium II
1 koło zadania treningowe issajewicz
zadania treningowe 2, zadania treningowa 1 rozwiązania
więcej podobnych podstron