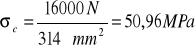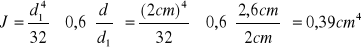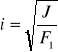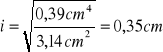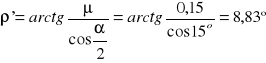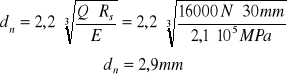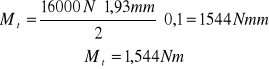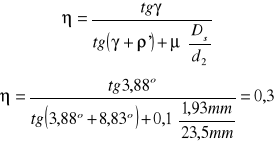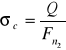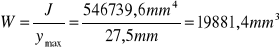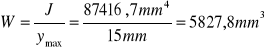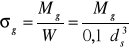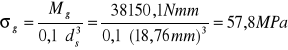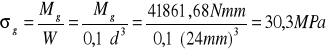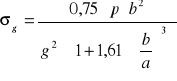POLITECHNIKA

Wydział Mechaniczny

Kierunek: Mechanika i Budowa Maszyn

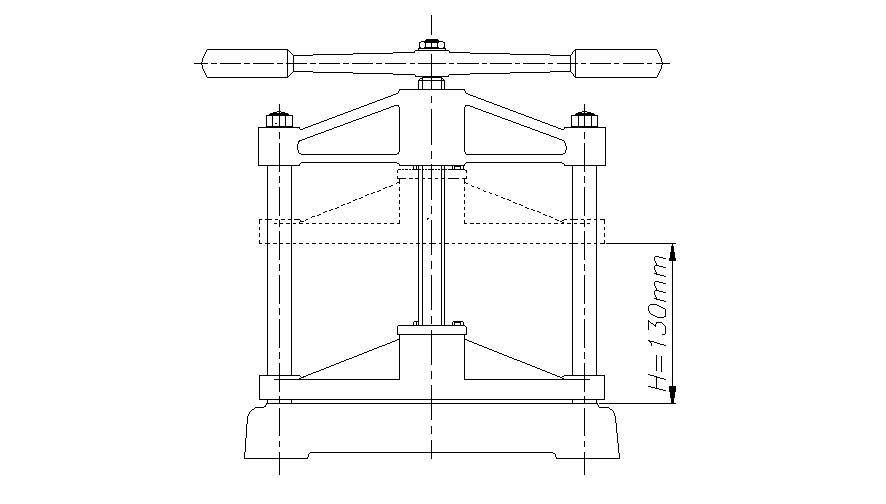
Dwusłupowa biurowa prasa śrubowa

Wykonał : Prowadzący :

DANE	OBLICZENIA I SZKICE	WYNIKI
F= 0,04 m^2 p= 400000 Pa	Założenia i wstępny szkic prasy Założenia do wstępnych obliczeń Zaprojektować biurową prasę śrubową o maksymalnym wzniosie H = 0,15 [m], czynnej powierzchni F = 0,20 x 0,20 =0,04 [m^2], oraz nacisku powierzchniowym p = 0,4 [MPa] . Jako materiał śruby przyjmuję stal 45 ulepszaną cieplnie. Wstępny schemat prasy Obliczenia śruby Obliczenia siły ściskającej śrubę: , gdzie: Q - siła nacisku obliczana ze wzoru :	Q = 16000N
d1 = 20 mm Q = 16000N F1 = 314 mm^2	Przyjmuję średnicę d1 = 20 mm , oraz gwint trapezowy symetryczny Tr 26 x 5 . Obliczenie pola powierzchni przekroju poprzecznego śruby Pole przekroju poprzecznego śruby F1 obliczamy z podanej wyżej zależności: Obliczenie naprężeń ściskających w rdzeniu śruby kc - dopuszczalne naprężenia ściskające wyznaczane z zależności : Re - granica plastyczności xe - współczynnik bezpieczeństwa	Gwint Tr 26x5; d = 26 mm; d2= 23,5 mm; d1 = 20 mm; α = 30^o F1= 3,14cm^2 σc= 50,96 MPa
Re= 420 MPa; RH= 358 MPa; xe= 2;	Warunek jest spełniony ponieważ : kc > σc	kc=210 MPa;
d1 = 2 cm; d = 2,6 cm	Obliczenie momentu bezwładności Moment bezwładności obliczamy ze wzoru :	J= 0,39 cm^4
J= 0,39 cm^4 F1= 3,14cm^2	Obliczenie ramienia bezwładności Ramię bezwładności obliczamy ze wzoru : gdzie: J - moment bezwładności , Po podstawieniu danych otrzymujemy :	i = 0,35 cm
λgr=100 α =1; lw=20cm: imin=0,35cm. λgr=100	Obliczenie smukłości pręta gdzie: α - współczynnik swobodnej długości pręta w zależności od rodzaju zamocowania lw - długość wyboczeniowa pręta i - promień bezwładności przekroju	λ = 57,14 λgr=100
λgr=100 RH= 358 MPa =a=420 MPa; =b= 0,62 MPa λ = 57,14	Obliczenie naprężeń krytycznych w śrubie: Ponieważ λ < λgr sprawdzamy warunek wytrzymałościowy na wyboczenie niesprężyste stosując wzór Tetmajera : gdzie : a,b - współczynniki uzależnione od własności materiału dobierane z tablic, (Re, RH, E)	σkr=384,57MPa
σkr=384,57MPa; σc= 50,96 MPa	Obliczenie rzeczywistego współczynnika bezpieczeństwa na wyboczenie Współczynnik xwyb obliczamy z niżej podanego wzoru:	xwyb=7,55
d2= 23,5 mm; p = 5mm Dla materiału śruby i nakrętki przyjmuję współczynnik tarcia μ = 0,15 α =30^o	Sprawdzenie samohamowności gwintu gdzie : P - skok gwintu Warunek samohamowności jest spełniony ponieważ : ρ' > γ	γ= ρ' =
Q=16000N; d2=23,5mm; γ= ; ρ' = .	Obliczenie momentu skręcającego śrubę Moment skręcający śrubę obliczam korzystając z następującego wzoru : gdzie : Q - siła działająca na śrubę; d2 - średnica podziałowa gwintu śruby; γ, ρ' - kąt wzniosu linii śrubowej gwintu i pozorny kąt tarcia	Ms=42,4Nm
Q = 16000N; Rs= 30mm; E= 2,1* 10^5MPa	Moment tarcia na kulistym końcu śruby Moment ten obliczamy stosując wzór Hertza : gdzie : Ds - średnica działania siły tarcia przy założeniu równomiernego nacisku na powierzchni μ - współczynnik tarcia powierzchni kulistej śruby o podkładkę gdzie : dn - średnica pola powierzchni docisku Rs - promień na kulistym końcu śruby	dn=2,9mm ;
dn = 2,9mm Q= 16000N; Ds = 1,93mm; Przyjmujmy współczynnik tarcia μ = 0,1 (stal - stal) Ms=25,9Nm Mt=1,544Nm	Mając wszystkie dane i podstawiając je do wzoru Hertza możemy obliczyć: Całkowity moment tarcia	Ds = 1,93mm. Mt=1,544Nm; Mc = 43,9 Nm
γ=3,88^o; ρ' = 8,83^o; μ =0,1; Ds = 1,93 mm; d2 = 23,5 mm.	Obliczenie sprawności mechanizmu śrubowego Sprawność η obliczamy ze wzoru :	η = 0,3
d = 26 mm; d1 = 20 mm;	Obliczenia nakrętki Obliczenia czynnej powierzchni jednego zwoju oraz ilość zwojów nakrętki Znając powierzchnię jednego zwoju możemy obliczyć ilość zwojów nakrętki n, korzystając ze wzoru:	Fn=216,66mm^2
Q = 16000N; pdop = 8 MPa; Fn =216,66 mm^2	gdzie : pdop - naciski dopuszczalne dla nakrętki	n = 9,4
d1 =20 mm H = 60 mm; P = 5 mm.	Obliczenia wysokości nakrętki Chcąc uzyskać dobre prowadzenie śruby w nakrętce obliczam wysokość nakrętki z zależności : Znając wysokość nakrętki H oraz skok gwintu P ilość zwojów nakrętki możemy obliczyć również z zależności :	H = 60 mm Przyjmuję ilość zwojów nakrętki n = 12
	Przyjęcie zewnętrznej średnicy nakrętki Przyjmuje zewnętrzną średnicę nakrętki równą 58 mm.
	Obliczenia naprężeń ściskających w nakrętce Naprężenia ściskające w nakrętce obliczam stosując wzór : gdzie : Fn2 - powierzchnia nakrętki gdzie : Dn - średnica zewnętrzna nakrętki D - średnica wewnętrzna nakrętki
Dn= 58 mm; D = 26 mm ; Q = 16000N; Fn2 = 2111 mm^2	stąd : Mając wszystkie dane możemy obliczyć naprężenia ściskające :	Fn2 = 2111 mm^2 σc = 7,6 MPa
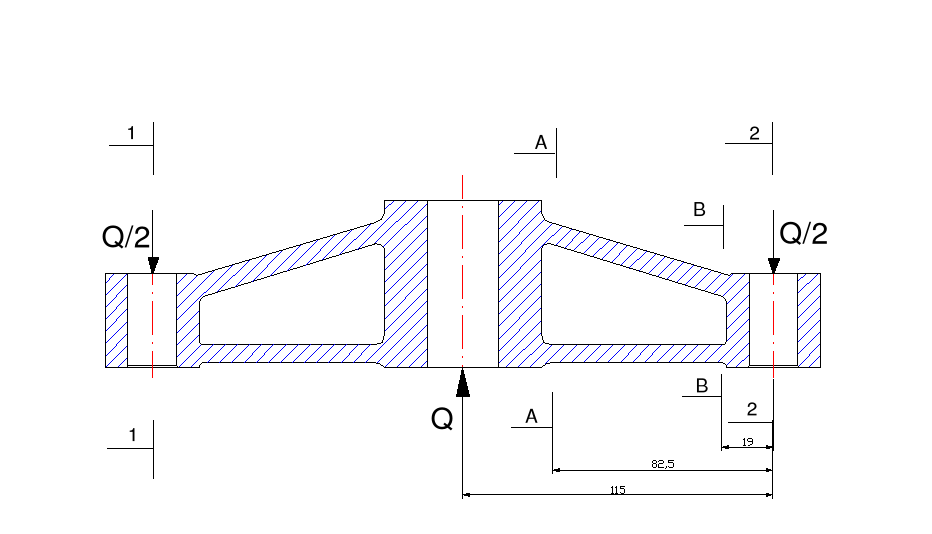
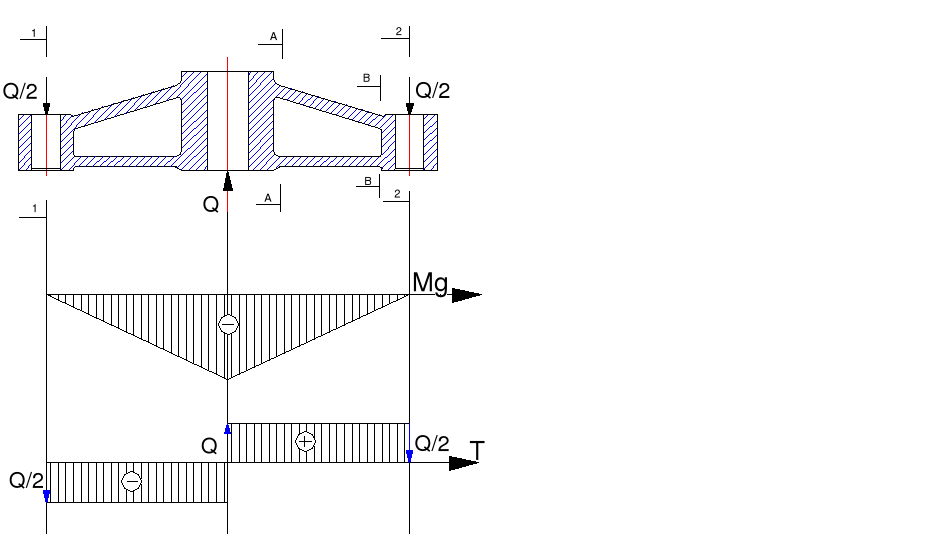
	Obliczenia belki górnej Szkic belki górnej Wobec dużej sztywności belki w porównaniu do słupków obliczamy ją jako swobodnie podpartą . Belkę obliczamy z warunku na zginanie gdzie: l - długość belki Naprężenia zginające belkę obliczamy korzystając z następującego wzoru : gdzie : W - wskaźnik wytrzymałości przekroju na zginanie
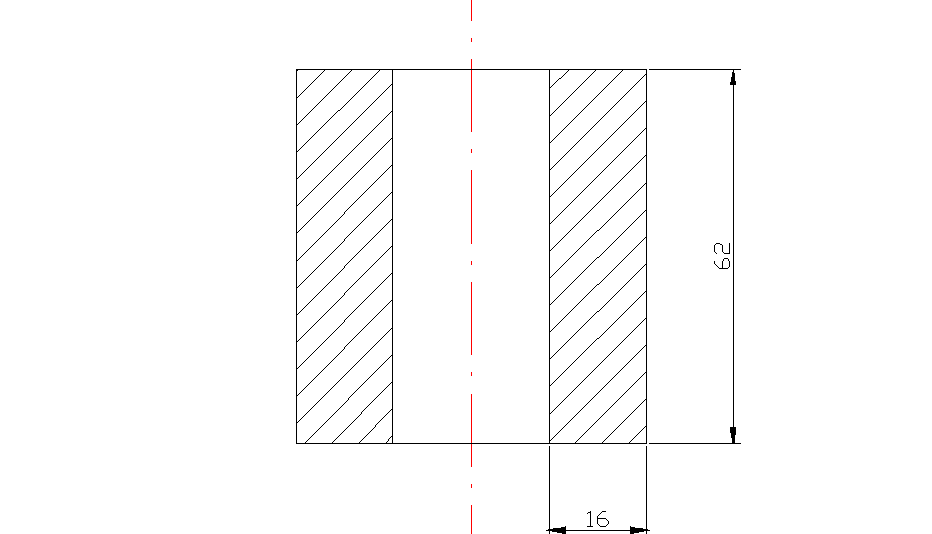
l = 230 mm; Q = 16000 N. b = 16 mm; h = 62 mm . Mg = 920000Nmm; W = 3481mm^3. Q = 16000 N; lA = 82,5 mm.	Obliczenia belki w przekroju środkowym: gdzie: b - szerokość belki w przekroju h - wysokość belki w przekroju Obliczenia belki w przekroju A - A gdzie: lA - długość belki do przekroju A - A	Mg = 920000Nmm W= =10250,67mm^3 σg = MPa Mg= 660000Nmm
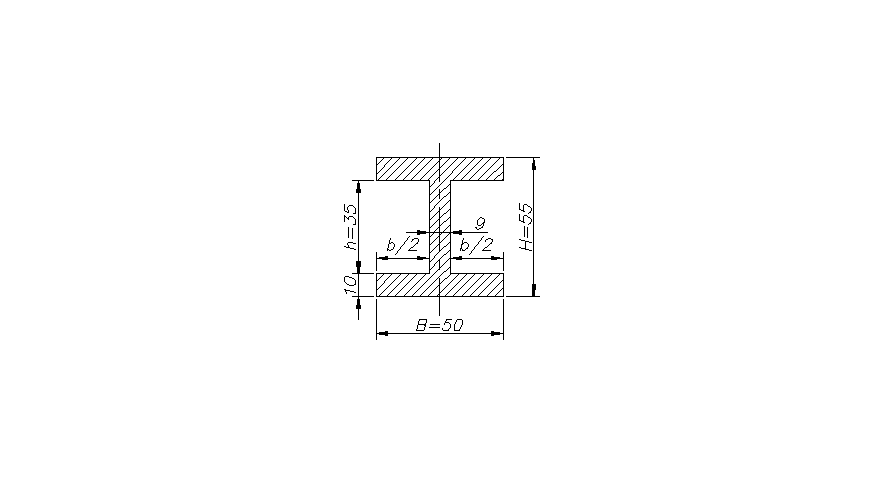
B = 50mm; H = 55mm; b = 41 mm; h = 35 mm. J = 546739,6mm^4; ymax = 27,5 mm . Mg= 660000Nmm; W= 19881,4mm^3. Q = 16000 N; lB = 19 mm.	gdzie: J - moment bezwładności ymax - najdalej oddalone włókna od osi przekroju poprzecznego belki Obliczenia belki w przekroju B - B gdzie: lB - długość próbki do przekroju B - B	J=546739,6mm^4 W= 19881,4mm^3 σg = 33,20 MPa Mg= 152000Nmm
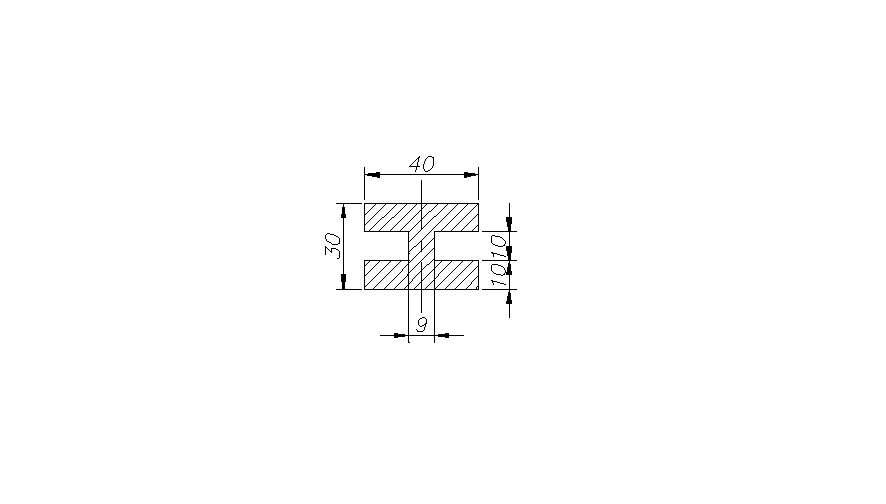
B = 40mm; H = 30mm; b = 31mm; h = 10 mm. J = 87416,7mm^4; ymax = 15 mm . Mg= 152000Nmm; W= 5827,8mm^3.		J = 87416,7mm^4 W = 5827,8mm^3 σg = 26,1 MPa
Q = 16000N Q = 16000N Q = 16000N	Obliczenie sił tnących: w przekroju środkowym w przekroju 1 - 1 w przekroju 2 - 2 Przedstawienie momentów gnących i sił tnących na wykresie Mgs = 920 Nm Ts = 16000 Mg1 = 0 T1 = - 8000N Mg2 = 0 T2 = 8000N MgA = 660 Nm MgB = 152Nm	Ts =16000N Ts = - 8000N Ts = 8000N
A1 = 144mm^2; Q = 16000N.	Obliczenia słupków Obliczanie naprężeń rozciągających w gwincie śruby M16 gdzie: A1 - pole powierzchni przekroju poprzecznego śruby	σr = 55,56 MPa
Ms=42380Nmm; L = 240 mm.	Obliczenie siły poziomej H w gwincie nakrętki Na słupek działa także siła pozioma H od momentu skręcającego w gwincie nakrętki i można ją obliczyć z następującego wzoru: gdzie: L - odległość między słupkami	H = 184,3 N
H = 184,3 N; h = 207mm.	Obliczenie momentu zginającego słupek gdzie: h - długość słupka	Mg=38150,1Nmm
Mg=38150,1Nmm; ds = 18,76 mm.	Obliczenie naprężeń gnących Do obliczeń naprężeń przyjmujemy jako średnicę obliczeniową średnią średnicę geometryczną słupka i naprężenia obliczamy z zależności: gdzie: ds - średnia średnica geometryczna słupka	ds = 18,76 mm σg = 57,8 MPa
Q = 16000N; d = 16mm.	Obliczenie naprężeń rozciągających słupek gdzie: A2 - pole przekroju poprzecznego słupka na średnicy 16 mm	σr = 39,79 MPa
σg = 57,8 MPa; σr = 39,79 MPa.	Suma naprężeń działających na słupek	σc=97,59MPa
Mc=43994Nmm; L = 380 mm.	Obliczenie pokrętła Obliczenie siły na jednym ręku przy dwustronnym uchwyceniu pokrętła gdzie: L - długość pokrętła	P = 115,64 N
P = 115,64 N; l = 181 mm. Mg=41861,68Nmm ; d = 24 mm	Obliczenie momentu zginającego i naprężeń gnących pokrętło gdzie: l - ramię działania siły	Mg=41861,68Nmm σg = 30,3 MPa
lo = 18mm b=5mm h=6,5mm z = 0,6; kc = 175MPa. Mc = 43994Nmm d = 18 mm P=4888N; h =5 ; ko = 105MPa . lo = 18 mm ; b = 5 mm.	Obliczenie połączenia wpustowego śruby z pokrętłem Wg normy PN - 70/M - 85005 dobieram wymiary poprzeczne wpustu bxh = 5x6,5 mm . Przyjmujemy, że wpust będzie wykonany ze stali St7, dla której kc = 175 MPa . Obliczam wartość dopuszczalnych nacisków powierzchniowych wg wzoru : gdzie: z - współczynnik określający warunki pracy połączenia Obliczenie siły P działającej na wpust korzystając ze wzoru: gdzie: d - średnica czopa śruby Znając wartość siły działającej na wpust oraz wymiary poprzeczne wpustu i wartość dopuszczalnych nacisków powierzchniowych możemy je sprawdzić na nacisk i na ścinanie: Sprawdzenie wpustu ze względu na nacisk powierzchniowy: Sprawdzenie wpustu ze względu na ścinanie: Dobieram wpust czółenkowy 5x6,5. Przyjmuję wpust pryzmatyczny 5x5x24.	bxh=5x6,5mm kt=kd 105MPa P = 4888N lo = 18mm
p = 0,4 MPa; b = 200 mm; a = 200 mm; g = 12 mm.	Obliczanie podstawy Podstawę obliczamy jako płytę prostokątną opartą na krawędzi i równomiernie obciążoną na powierzchni (w obliczeniach uproszczonych nie uwzględniamy żeber wzmacniających). Obliczenie naprężeń gnących Obliczeń dokonujemy wg zależności : gdzie: p - naciski powierzchniowe b, a, g - wymiary podstawy	σg = 31,9 MPa

1

- 14 -