Politechnika Częstochowska

Wydział Elektryczny

Katedra Elektrotechniki

Zakład Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Wyznaczanie charakterystyk magnesowania ferromagnetyków

Częstochowa 2004

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie pętli histerezy blachy transformatorowej oraz zbadanie zjawisk towarzyszących nasyceniu rdzenia.

2. Wiadomości podstawowe

2.1. Charakterystyki magnesowania

Cewka z rdzeniem ferromagnetycznym stanowi w obwodzie elektrycznym element nieliniowy. Jest to związane z nieliniowością charakterystyki magnesowania rdzenia B = f(H). Charakterystyka ta jest ponadto niejednoznaczna i w ogólności zależy od całej historii magnesowania rdzenia. Zależność własności układu od jego historii nazywa się histerezą.

Własności magnetyczne ferromagnetyka określone są jego charakterystykami magnetycznymi, przedstawiającymi zależność indukcji magnetycznej B od natężenia pola magnetycznego H w rdzeniu. Wyróżnia się następujące charakterystyki magnesowania:

• krzywa pierwotna magnesowania,

• statyczna pętla histerezy magnetycznej,

• statyczna podstawowa krzywa magnesowania,

• dynamiczna pętla histerezy magnetycznej,

• dynamiczna krzywa magnesowania.

Krzywą pierwotną magnesowania otrzymuje się dla próbki ferromagnetyka magnesowanej po raz pierwszy od stanu H = 0 i B = 0 przy monotonicznie rosnącym natężeniu pola H (rys. 1). Można na niej wyróżnić cztery charakterystyczne części:

• odcinek 0-1, zwany dolnym zagięciem charakterystyki, na którym przenikalność magnetyczna  rośnie,

• odcinek 1-2, będący w przybliżeniu odcinkiem prostoliniowym o nachyleniu  ≈ const,

• odcinek 2-3, zwany górnym zagięciem charakterystyki, na którym  maleje do ₀ w miarę jak zbliżamy się do punktu 3,

• odcinek powyżej punktu 3, będący obszarem nasycenia; na tym odcinku krzywa ma stałe nachylenie odpowiadające  = ₀ i dalszy wzrost natężenia pola H powoduje nieznaczny tylko przyrost indukcji B wg wzoru B = const + ₀H.

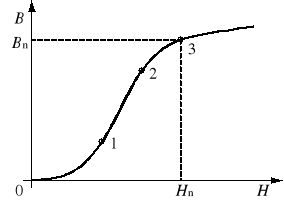
Rys. 1. Krzywa pierwotna magnesowania (H_n - natężenie nasycenia, B_n - indukcja nasycenia)

Dokonując wielokrotnego przemagnesowania ferromagnetyka od wartości -H_max do +H_max
i z powrotem od +H_max do -H_max otrzymuje się symetryczną krzywą zamkniętą, zwaną pętlą histerezy (rys. 2). Pętla histerezy dla H_max = H_n odcina na osiach dwa charakterystyczne odcinki:

• odcinek 0A = 0A′, którego długość jest proporcjonalna do indukcji remanentu B_r (indukcji szczątkowej, pozostałości magnetycznej), tj. indukcji występującej przy braku natężenia zewnętrznego pola magnetycznego,

• odcinek 0C′ = 0C, którego długość jest proporcjonalna do natężenia koercji H_k (natężenia powściągającego), tj. zewnętrznego natężenia pola magnetycznego potrzebnego do całkowitego rozmagnesowania.

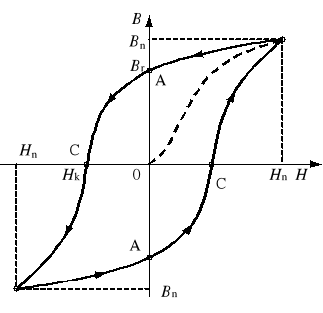
Rys. 2. Pętla histerezy otrzymana dla wielokrotnego przemagnesowania od -H_n do +H_n i z powrotem

Kształt pętli histerezy zależy od wielu czynników, m.in. od składników materiału ferromagnetycznego i sposobu jego obróbki. Ze względu na szerokość pętli materiały ferromagnetyczne dzielimy na magnetycznie twarde i magnetycznie miękkie.

Materiały magnetycznie twarde posiadają szeroką pętlę histerezy i charakteryzują się dużą wartością H_k i zwykle dużą wartością B_r. Nadają się one do zastosowań w obwodach prądu stałego oraz do budowy magnesów trwałych. Materiały magnetycznie miękkie posiadają wąską pętlę histerezy i charakteryzują się małą wartością H_k i zwykle dużą wartością B_r. Stosowane są w urządzeniach prądu zmiennego. Taki zakres zastosowań wynika z tego, że pole pętli histerezy jest miarą energii przypadającej na jednostkę objętości, potrzebnej do jednego cyklu przemagnesowania danego materiału. Magnesy trwałe powinny mieć jak największą energię, aby nie ulegały łatwo rozmagnesowaniu, stąd do ich budowy wykorzystuje się materiały magnetycznie twarde; z kolei w urządzeniach prądu zmiennego straty na przemagnesowanie powinny być jak najmniejsze, zatem w tym przypadku stosuje się materiały magnetycznie miękkie.

Powtarzając proces cyklicznego magnesowania materiału ferromagnetycznego dla różnych wartości maksymalnych H_max, otrzymuje się rodzinę pętli histerezy oraz graniczną pętlę histerezy, tj. pętlę o największym polu powierzchni (rys. 3). W zależności od sposobu przemagnesowania materiału ferromagnetycznego - prądem stałym lub przemiennym - otrzymuje się statyczną bądź dynamiczną pętlę histerezy. Statyczna pętla histerezy magnetycznej otrzymywana jest przy powolnej zmianie pola magnetycznego. Statyczna podstawowa krzywa magnesowania jest miejscem geometrycznym wierzchołków rodziny statycznych pętli histerezy (rys. 3). Praktycznie niewiele różni się ona od krzywej pierwotnej magnesowania

Dynamiczna pętla histerezy jest zależnością między uśrednioną w przekroju blachy ferromagnetycznej wartością chwilową indukcji magnetycznej B(t), a chwilową wartością natężenia pola magnetycznego H(t) na powierzchni blachy podczas przemagnesowania blachy prądem przemiennym. Jeśli porównamy statyczną i dynamiczną pętlę histerezy, otrzymaną przy takim samym natężeniu H_max, to stwierdzimy, że różnią się one dość znacznie zarówno pod względem kształtu jak i pola powierzchni. Kształt dynamicznej pętli zależy nie tylko od właściwości samego materiału ferromagnetycznego (jako ma to miejsce w przypadku pętli statycznej), ale również od struktury próbki, od jej wymiarów, a nawet od elektrycznych parametrów obwodu, w którym została ona pomierzona (np. od częstotliwości, kształtu prądu magnesowania). Wobec zwiększonych strat energii, spowodowanych prądami wirowymi i opóźnieniem magnetycznym (wynikającym z nienadążania zmian B za polem H w wyniku oporu stawianego przez domeny podczas ich reorientacji), dynamiczna pętla histerezy ma większe pole powierzchni niż pętla statyczna. Dynamiczna krzywa magnesowania jest miejscem geometrycznym wierzchołków rodziny dynamicznych pętli histerezy dla ustalonej częstotliwości.

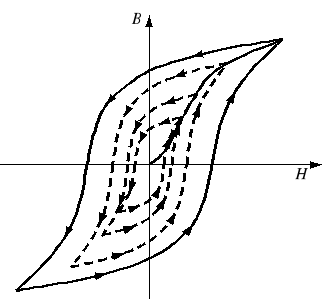
Rys. 3. Rodzina pętli histerezy i podstawowa krzywa magnesowania

2.2. Wyznaczanie dynamicznej pętli histerezy

Jedną z najczęściej spotykanych metod wyznaczania dynamicznej pętli histerezy jest metoda oscylograficzna. Schemat układu pomiarowego przedstawiono na rysunku 4.

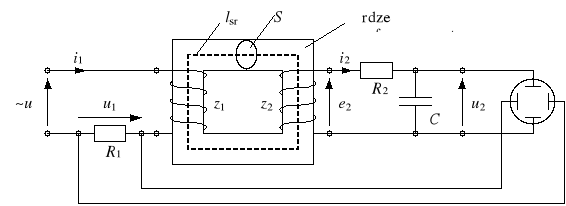
Rys. 4. Schemat układu do wyznaczania dynamicznej pętli histerezy metodą oscylograficzną

Pętlę histerezy rdzenia otrzymujemy na ekranie oscyloskopu doprowadzając do jego płytek odchylania poziomego sygnał napięciowy proporcjonalny do natężenia pola magnetycznego, a do płytek odchylania pionowego - sygnał napięciowy proporcjonalny do indukcji magnetycznej.

Napięcie u₁ proporcjonalne do natężenia pola magnetycznego H(t) w rdzeniu otrzymuje się
z opornika R₁ połączonego szeregowo z uzwojeniem magnesującym (wartość rezystancji R₁ powinna być mniejsza od impedancji cewki magnesującej). Korzystając z oznaczeń podanych na rysunku 4, można zapisać zależność wynikającą z prawa przepływu:

gdzie z₁ - liczba zwojów uzwojenia pierwotnego, l_sr - średnia droga strumienia magnetycznego, k₁ - współczynnik równy

Zgodnie z prawem indukcji elektromagnetycznej

gdzie z₂ - liczba zwojów cewki drugiej, S - pole przekroju poprzecznego rdzenia. Aby otrzymać sygnał proporcjonalny do chwilowej wartości indukcji magnetycznej B, sygnał e₂ należy podać na człon całkujący. Można do tego celu wykorzystać układ (R₂, C) w postaci podanej na rysunku 4. Jeśli R₂ >> 1/C i R₂ >> r, gdzie  - pulsacja podstawowej harmonicznej siły elektromotorycznej e₂, r - rezystancja drugiej cewki, to można zapisać

skąd

przy czym

2.3. Przebieg prądu w cewce z rdzeniem ferromagnetycznym

Jeśli cewkę z rdzeniem ferromagnetycznym zasilimy napięciem sinusoidalnie zmiennym, to prąd płynący przez cewkę nie będzie sinusoidalny. Konstrukcję przebiegu prądu pokazano na rysunku 5a. Rysujemy pętlę histerezy, obok rysujemy przebieg napięcia oraz indukcji. Jeśli indukcja ma przebieg sinusoidalny, to napięcie zgodnie ze wzorem

będzie mieć przebieg kosinusoidalny. Pod pętlą histerezy rysujemy układ współrzędnych (i, t), przy czym oś prądu rysujemy równolegle do osi H, a oś czasu - w dół. Dla każdego czasu wyznaczamy indukcję, z pętli histerezy odczytujemy odpowiadające jej natężenie pola magnetycznego
i równocześnie natężenie prądu (który jest proporcjonalny do H). W układzie (i, t) zaznaczamy punkt odpowiadający danemu czasowi i prądowi. Otrzymane punkty łączymy.

Przykładowo dla czasu t₁ znajdujemy punkt C na przebiegu indukcji, oraz odpowiadający mu punkt C na pętli histerezy, a następnie zaznaczmy punkt C w układzie (i, t). Zauważmy, że dla czasu t₂, choć indukcja jest taka jak dla t₁, otrzymuje się inną wartość prądu i, gdyż dla malejących indukcji znajdujemy się na górnej gałęzi pętli histerezy (punkt E).

Gdy pętla histerezy jest wąska, można pominąć zjawisko histerezy i konstrukcja z rysunku 5a upraszcza się do konstrukcji z rysunku 5b. Z obydwu rysunków widać, że prąd płynący przez cewkę z rdzeniem ferromagnetycznym jest znacznie odkształcony od prądu sinusoidalnego.

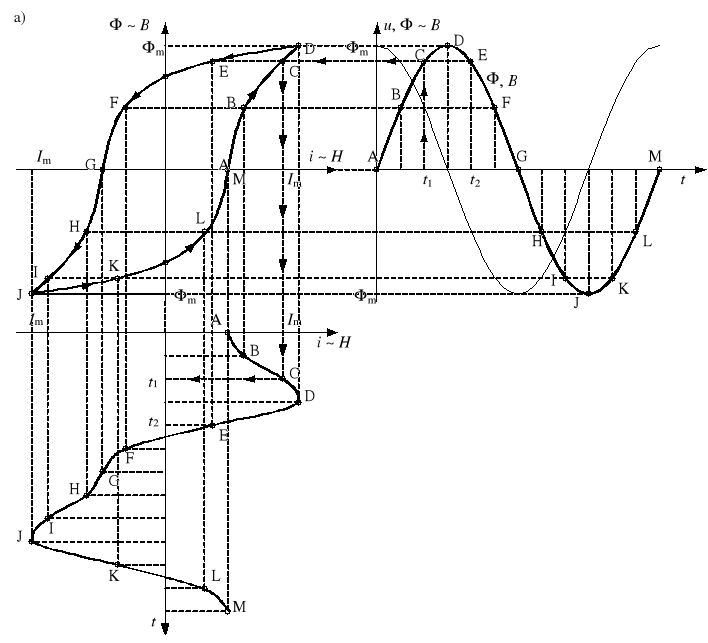
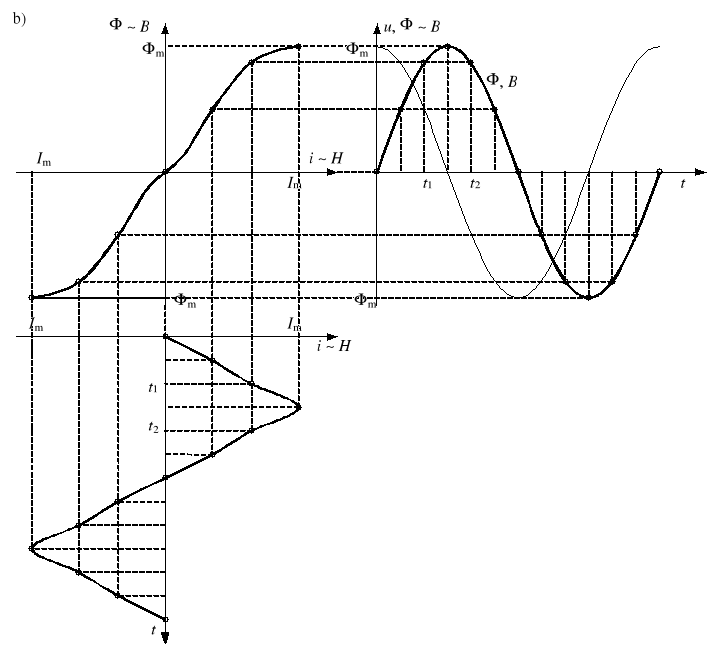
Rys. 5. Konstrukcje przebiegu prądu w cewce z rdzeniem ferromagnetycznym: dokładna (a) i uproszczona (b)

2.4. Wzmacniacz magnetyczny

Elementy ferromagnetyczne stanowią dla prądu przemiennego znaczną reaktancję, ale tylko przy napięciach mniejszych od pewnej wartości U_n, przy której następuje nasycenie rdzenia (X jest proporcjonalne do indukcyjności L, która jest proporcjonalna do przenikalności względnej _r, przyjmującej duże wartości poza obszarem nasycenia i wartość równą 1 w obszarze nasycenia). W zakresie zmian napięcia u na elemencie ferromagnetycznym od 0 do U_n charakterystyka magnesowania jest zbliżona do linii prostej i sinusoidalnym zmianom indukcji magnetycznej (a więc i napięcia) odpowiada prawie sinusoidalny przebieg natężenia pola (a więc i prądu) - rys. 6, krzywa 1 (zjawisko histerezy pomijamy). Napięcie U_n (wartość skuteczna) odpowiada maksymalnej wartości indukcji w rdzeniu B_n, czyli

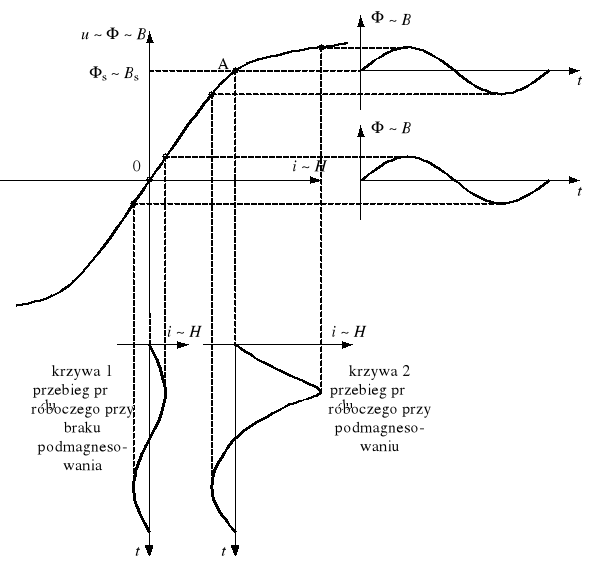
Rys. 6. Przebiegi prądu i strumienia w przypadku braku podmagnesowania i z podmagnesowaniem

Przekroczenie napięcia U_n prowadzi do nasycenia rdzenia przed upływem danego półokresu napięcia zasilania i punkt pracy przechodzi na poziomą część charakterystyki magnesowania, co znajduje odbicie w znacznym wzroście wartości natężenia pola magnetycznego (a tym samym prądu). Ten sam efekt nasycenia rdzenia można uzyskać również dla U < U_n, jeśli do rdzenia wprowadzimy dodatkowy strumień magnetyczny, przesuwający średni punkt pracy z punktu 0 do punktu A (rys. 6). Można w tym celu zastosować układ złożony z transformatora, którego jedno uzwojenie (robocze) zasilane jest napięciem sinusoidalnym, a drugie (sterujące) zasilane jest ze źródła napięcia stałego (rys. 7). W obwodzie sterującym znajduje się ponadto dławik, ograniczający wartość prądu pulsacyjnego zaindukowanego w uzwojeniu sterującym z_s na skutek czasowych zmian strumienia w rdzeniu.

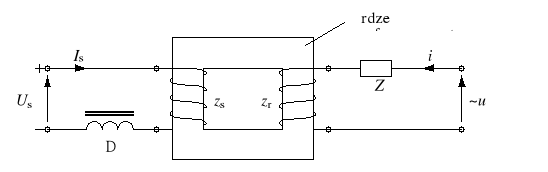
Rys. 7. Prosty wzmacniacz magnetyczny

Jeżeli prąd sterujący I_s jest równy zeru, a amplituda napięcia doprowadzonego do uzwojenia roboczego jest na tyle mała, że nie nasyca rdzenia, to sinusoidalnym zmianom napięcia
w uzwojeniu roboczym odpowiada w przybliżeniu sinusoidalny przebieg prądu roboczego. Ponadto ze względu na dużą przenikalność magnetyczną, odpowiadającą dużemu nachyleniu krzywej magnesowania, prąd roboczy jest niewielki (rys. 6, krzywa 1).

Gdy w uzwojeniu sterującym popłynie prąd I_s, wywoła on dodatkowy strumień _s i indukcję B_s. Ponieważ w pobliżu punktu A krzywa magnesowania jest bardziej płaska, strumień w uzwojeniu roboczym wywoła większe zmiany natężenia pola magnetycznego i prądu w uzwojeniu roboczym niż w przypadku I_s = 0 (rys. 6 - krzywa nr 2). Na skutek asymetrii krzywej magnesowania względem punktu pracy A krzywa natężenia pola H i prądu roboczego jest asymetryczna.

Reasumując, wzrost prądu sterującego I_s powoduje wzrost amplitudy prądu roboczego oraz jego odkształcenie. Zjawisko to wykorzystano do budowy wzmacniaczy magnetycznych,
w których za pośrednictwem prądu I_s steruje się wartością prądu roboczego bez zmiany napięcia zasilania uzwojenia roboczego. Każdy taki wzmacniacz posiada charakterystykę wartości skutecznej prądu roboczego I w funkcji prądu sterującego I_s (tj. I = f(I_s)). Przykładową charakterystykę pokazano na rysunku 8.

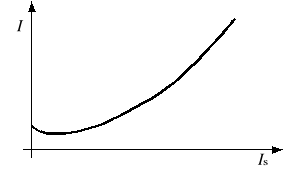
Rys. 8. Typowa charakterystyka wzmacniacza magnetycznego

Taki prosty układ, jak na rysunku 7, ma szereg wad:

• konieczność stosowania w obwodzie dławika o dużej reaktancji,

• duża zawartość harmonicznych w prądzie roboczym,

• charakterystyka sterowania I = f(I_s) jest silnie nieliniowa (rys. 8),

• układ cechuje duża bezwładność.

Dla wyeliminowania tych wad w praktyce stosuje się bardziej złożone układy.

Oprócz wzmacniaczy magnetycznych również inne urządzenia wykorzystują zależność funkcyjną między prądem I_s i prądem roboczym I, np. transduktory - urządzenia do pomiaru dużych prądów stałych za pośrednictwem prądu zmiennego.

3. Przebieg ćwiczenia

3.1. Badanie układu bez podmagnesowania prądem stałem

• Zestawić układ wg schematu z rysunku 9, przy czym przełącznik W zostawić otwarty,

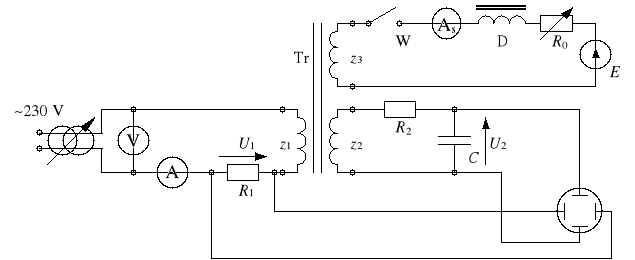
Rys. 9

• Przed przystąpieniem do obserwacji nastawić autotransformatorem napięcie rzędu kilku woltów i sprawdzić, czy napięcia odchylające przyłożone do obu par płytek oscyloskopu są w przybliżeniu jednakowe; sprawdzenie przeprowadzić przez porównanie długości linii poziomej
  i pionowej zakreślanych kolejno na ekranie w czasie doprowadzania do odpowiednich gniazdek oscyloskopu na przemian napięć U₁ i U₂,

• Zwiększając powoli napięcie autotransformatora obserwować pętlę histerezy i wyznaczyć napięcie zasilania U_n, przy którym następuje nasycenie rdzenia; odrysować z ekranu oscyloskopu pętlę histerezy zapisując jednocześnie nastawy pokręteł wzmocnienia tych napięć (tabela 1),

• Ustawić napięcie na zasilania kolejno na 0,5U_n, 0,75U_n i 1,5U_n, odrysowując za każdym razem pętlę (na tym samym rysunku co poprzednio) i notując nastawy pokręteł m_x i m_y.

Tabela 1 (Parametry układu)

z1	z2	R1	R2	C	S	lsr
Wartości parametrów (w górnym wierszu należy wpisać wartości odczytane z elementów układu, gdyż podane niżej wartości mogą być nieaktualne)
1000	1220	5 	100 k	10 F	26 cm	10 cm^2

Tabela 2

Lp.	Pomiary			Obliczenia
		U	Ymax	Xmax	U1	U2	Hmax	Bmax
		V	mm	mm	V	V	A/m	T
1	Un =
2	0,5Un
3	0,75Un
4	1,5Un

Wzory do obliczeń:

3.2. Badanie układu z podmagnesowaniem prądem stałym

• Nastawić R₀ na wartość maksymalną i ustawić wyłącznik W w pozycji zamkniętej,

• Przy napięciu 0,5U_n oraz przy wskazanych przez prowadzącego dwóch wartościach prądu sterującego I_s przerysować oscylogramy pętli histerezy,

• Z kolei przełączyć wyłącznik W do pozycji otwartej i ustawić takie napięcie zasilania, aby prąd I był równy wartości wskazanej przez prowadzącego (zwykle 25 mA); zanotować wskazania przyrządów dla I_s = 0 (tabela 3),

• Ponownie zamknąć wyłącznik i powoli zmniejszając wartość rezystora R₀ doprowadzić do stanu, w którym prąd I wzrośnie o wartość zadaną przez prowadzącego (zwykle 25 mA),

• Pomiary kontynuować, zmniejszając wartość rezystora R₀ tak, aby prąd I wzrastał o uprzednio zadaną wartość (UWAGA: wartość rezystora R₀ należy zmniejszać bardzo powoli, bacznie obserwując wskazania przyrządów; pomiary zakończyć, gdy prąd I lub I_s osiągnie maksymalną dopuszczalną wartość).

Tabela 3

Lp.	1	2	3	4	5	6	7	8	9
Is
I
I/Is
I/Is

4. Opracowanie sprawozdania

1. Cel ćwiczenia.

2. Schematy pomiarowe i tabele wyników.

3. Parametry i dane znamionowe zastosowanych przyrządów.

4. Przykłady obliczeń poszczególnych wartości podanych w tabelach.

5. Zamieścić, wyskalować i omówić otrzymane oscylogramy pętli histerezy.

6. Wyznaczyć przybliżoną podstawową charakterystykę magnesowania.

7. Na podstawie charakterystyki magnesowania skonstruować i wykreślić ch-kę  = f(H).

8. Wykreślić charakterystykę I = f(I_s) oraz wzmocnienie prądowe I/I_s = f(I_s).

9. Wnioski.

5. Pytania sprawdzające

1. Na czym polega zjawisko histerezy magnetycznej?

2. Co to jest statyczna pętla histerezy, a co dynamiczna?

3. Jakie czynniki wpływają na kształt dynamicznej pętli magnesowania? Dlaczego jest ona szersza od pętli statycznej?

4. Co to jest dynamiczna krzywa magnesowania?

5. Omówić charakterystyczne punkty pętli histerezy.

6. Co to są materiały magnetycznie miękkie i magnetycznie twarde? Podać zastosowania obydwu rodzajów materiałów.

7. Narysować i objaśnić układ do zdejmowania pętli histerezy.

8. Objaśnić rolę układu RC w układzie do zdejmowania pętli histerezy.

9. Omówić sposób konstrukcji przebiegu prądu w cewce z rdzeniem ferromagnetycznym, zasilanej napięciem sinusoidalnie zmiennym.

10. Omówić zasadę działania wzmacniaczy magnetycznych.

11. Jaką rolę spełnia dławik w obwodzie sterującym wzmacniacza magnetycznego?

Literatura

[1] Bolkowski S.: Elektrotechnika teoretyczna, tom I - teoria obwodów elektrycznych, WNT,
W-wa 1986, ss. 185-190, 486-492, 519-523.

[2] Kurdziel R.: Podstawy elektrotechniki, WNT, W-wa 1972, ss. 240-246.

[3] Lubelski K.: Podstawy elektrotechniki, część 2, skrypt Politechniki Częstochowskiej, Cz-wa 1973, ss. 184-190.

Wyznaczanie charakterystyk magnesowania ferromagnetyków

10

Politechnika Częstochowska, Wydział Elektryczny, Katedra Elektrotechniki

---