10.2. Losowe wymuszenia wewnętrzne i zewnętrzne w wyniku sprzężenia drgań pojazdu (na nierównościach drogi) z drganiami skrętnymi w układach transmisji momentu trakcyjnego na koła.

10.2.1. Funkcja położenia sprzęgła.

Funkcja położenia sprzęgła (dowolnego rodzaju) opisuje różnicę kątowych położeń odcinków wałów połączonych tym sprzęgłem. Funkcje =-; położenia sprzęgieł odsuwnych podano w p. 8.3 i 8.4. Funkcje położenia sprzęgieł wychylnych podano w tabeli 8.7, zamieszczonej w p. 8.5.3. Formalizm wpisania funkcji położenia sprzęgieł do matematycznych modeli konturów dynamicznych jak też do szeregowych struktur układów transmisji momentu został przedstawiony w p. 11.1. 11.2 i 11.3.

10.2.2. Funkcja położenia przekładni.

Funkcja położenia przekładni opisuje dodatkowy kąt obrotu wałka wejściowego (napędzającego). Ten dodatkowy kąt obrotu występuje w układzie napędowym wyłącznie w następstwie zmiany położenia obudowy przekładni. Podczas ruchu pojazdu trakcyjnego jest to nieuchronna, losowa, kompensacyjna zmiana położenia wywołana ruchem kół zestawu po nierównościach toru względem ramy pojazdu, do której przyłączone jest ramię reakcyjne obudowy przekładni. Zmiana położenia zestawu względem ramy jest równa ugięciu usprężynowania osi zestawu od położenia statycznego. Podczas ruchu pojazdu, omawiany dodatkowy kąt obrotu wałka wejściowego wywołuje dodatkowe zaburzenie dynamiczne nakładające się na (quasistatycznie pojmowane) obciążenie trakcyjne. Funkcja położenia przekładni określa stopień sprzężenia wymuszenia drgań skrętnych w układzie napędowym z pionowymi, losowymi ugięciami usprężynowania osi. Jest to sprzężenie bardzo szkodliwe.

Przekładnia płaska, w wykonaniu dwukołowym, została przykładowo przedstawiona na rysunku 10.1. Rozważymy zmianę kątowego położenia koła z2 wywołaną uniesieniem zestawu względem nieruchomej ramy wózka (lub ugięciem ramy w stosunku do nieruchomego zestawu). Rozważymy dwie fazy położeń. W obydwóch fazach kąt obrotu zestawu 1 potraktujemy jako równy zeru.

W fazie 2, ugięcie e = e(t), wywołało kąt obrotu * obudowy przekładni. Kąt obrotu 2 zębnika z2 w stosunku do obudowy przekładni wynosi

Całkowity, dodatkowy (pasożytniczy), kąt obrotu zębnika w stosunku do osi zestawu jest sumą kąta obrotu obudowy całej przekładni * (wraz z tym zębnikiem) oraz kąta obrotu zębnika w stosunku do obudowy przekładni. Ten całkowity, dodatkowy kąt obrotu zębnika nazywamy funkcją położenia przekładni p.

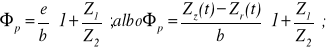
(10.6)

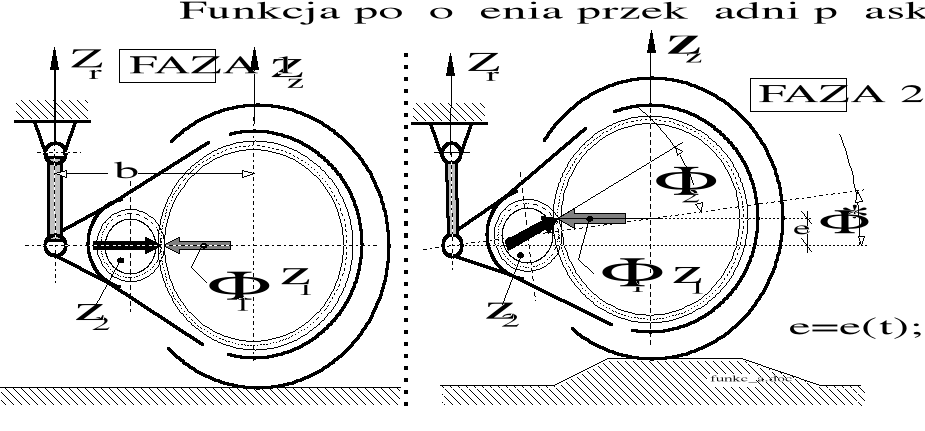
Rysunek 10. 1. Schemat przekładni płaskiej na nierówności toru.

Podczas ruchu pojazdu w torze, pasożytnicze zaburzenie ruchu zębnika nakłada się na ruch trakcyjny.

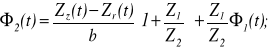
(10.7)

Pierwszy człon, po prawej stronie znaku powyższej równości, opisuje funkcję położenia przekładni; drugi człon - ruch trakcyjny.

Podobne zjawisko występuje w osiowych przekładniach kątowych.

Obciążenia płaskiej przekładni napędu osi lokomotywy.

Schematy dwukołowej i trójkołowej przekładni napędu osi lokomotywy, użyteczne przy modelowaniu dynamiki układu napędowego, przedstawiono na rysunku 10.3.

Z rysunku 10.3. wynikają następujące konstatacje praktyczne:

Działające na przekładnię dwukołową momenty zewnętrzne M1 i M2 mają zwroty zgodne.

Działające na przekładnię trójkołową momenty zewnętrzne M1 i M2 mają zwroty przeciwne.

Przy takich samych obciążeniach trakcyjnych wieszaki przekładni dwukołowej są obciążone bardziej niż wieszaki przekładni trójkołowej:

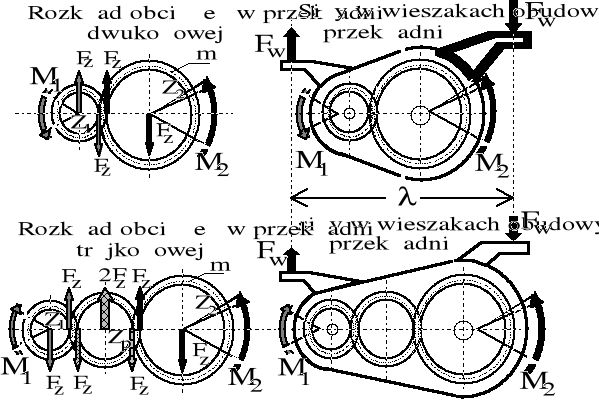
Rysunek 10.2. Schematy obciążeń płaskiej przekładni dwukołowej i trójkołowej.

Trakcyjne składowe obciążenia wieszaków przekładni dwukołowej:

(10.8)

Trakcyjne składowe obciążenia wieszaków przekładni trójkołowej:

(10.9)

W obrębie obudowy przekładni, wszystkie siły międzyzębne i łożyskowe, wzajemnie równoważą się.

Koło pośrednie Zp ma zęby obciążone w cyklu obustronnym symetrycznym; każdy ząb, na 1 obrót koła, podlega dwukrotnemu obciążeniu impulsowemu o zmiennym znaku.

Koła Z1 i Z2 mają zęby obciążone w cyku jednostronnym; każdy ząb, na 1 obrót koła, podlega jednokrotnemu obciążeniu impulsowemu.

Przekładnia kątowa została przedstawiona na rysunku 10.3.

Moment napędowy M2, pochodzący od zawieszonego na ramie silnika, przyłożony na wałku wejściowym przekładni, wywołuje nieznaczną asymetrię

Q obciążenia łożysk osiowych zestawu kół.

W przekładni kątowej mamy dwie możliwości (odmiany) konstrukcyjnego rozwiązania przyłączenia ramienia reakcyjnego obudowy przekładni do ramy wózka (pojazdu).

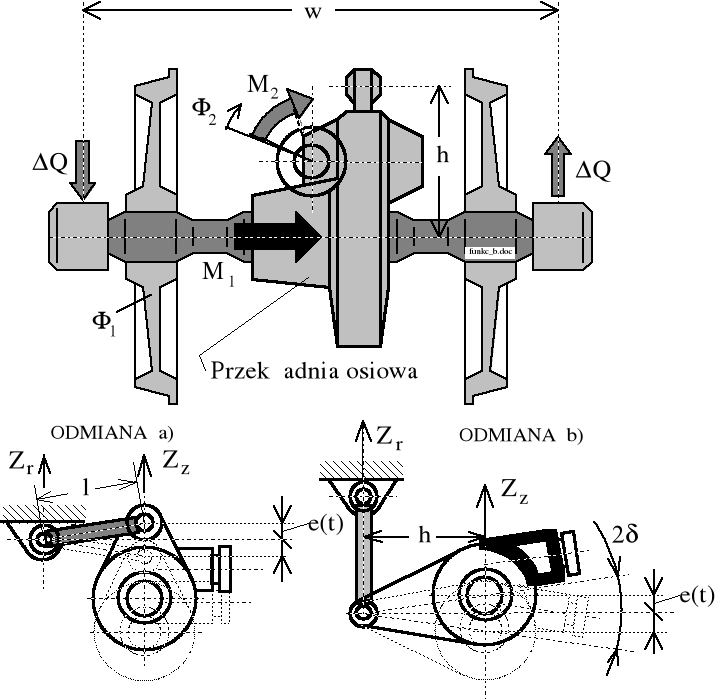
Rysunek 10.3. Schemat przekładni kątowej na nierówności toru.

ODMIANA a):

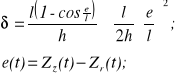
(10.10)

gdzie: - kąt obrotu korpusu przekładni:

Na podstawie wyżej przedstawionej zależności (e), możemy napisać wzór opisujący funkcję położenia przekładni:

(10.11)

gdzie:
- przełożenie przekładni

ODMIANA b): p = i; e/h;

(10.12)

Celowość stosowania wyłącznie odmiany a) jest, w świetle powyższych wzorów, oczywista.

10.2.3. Funkcja przestrzennej konfiguracji wału ("funkcja korby").

Przestrzenna konfiguracja wału przegubowego została pokazana na rysunku 8.65 sporządzonym dla celów analitycznych. Dla zilustrowania fizycznej istoty "funkcji korby" należy na środkowy odcinek wału przegubowego spojrzeć w ujęciu przestrzennym, jako na przekątną prostopadłościanu, według rysunku 10.4.

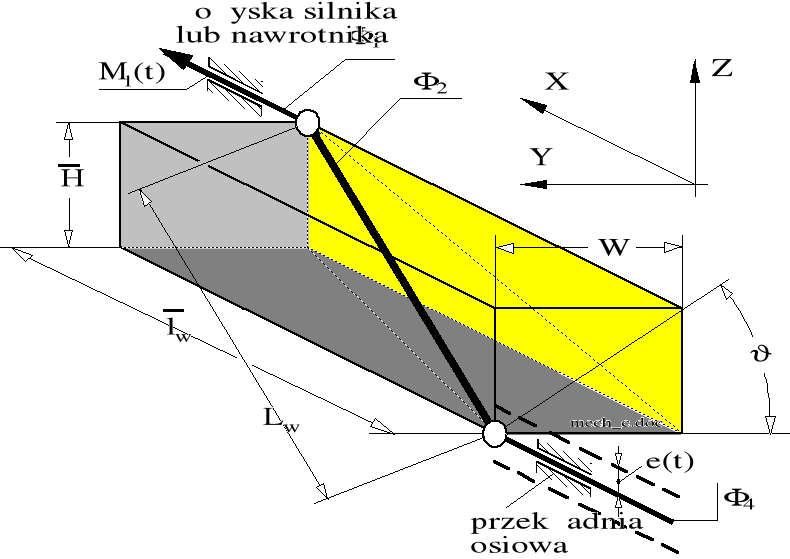
Rysunek 10.4. Przestrzenna konfiguracja wału przegubowego.

Funkcja przestrzennej konfiguracji wału przegubowego dotyczy wyłącznie przypadku zastosowania sprzęgieł nierównobieżnych, czyli wyróżniających się niezerowymi funkcjami położenia.

W przypadku przestrzennego wału przegubowego posadowionego na przekątnej prostopadłościanu
postępowe przemieszczenia e(t) przekładni osiowej w płaszczyźnie ZX wywołują zmianę wysokości prostopadłościanu
a tym samym zmianę kątów załamania wałów w sprzęgłach wychylnych. Przy sprzęgłach równobieżnych występujący w wale silnika (lub nawrotnika) dodatkowy kąt obrotu

wywołany przez "efekt korby" jest tylko pozorny. Jeżeli kąt obrotu wału 4=0, a sprzęgła są równobieżne, to niezależnie od zmienności wartości e(t), zawsze kąt
=0.

Jeżeli natomiast sprzęgła są nierównobieżne zaś odcinki wału "1" i "4" nie leżą na osiach do siebie równoległych, to wał przestaje być płaski (nie ma wspólnej płaszczyzny, nachylonej pod kątem , na której leżą wszystkie trzy odcinki wału "1", "2" i "4" - jak na rysunku 10.4). W takich okolicznościach, zmienne (w czasie) w poszczególnych sprzęgłach, kąty załamania osi odcinków wałów wywołają określone następstwa kinematyczne w ruchu obrotowym układu napędowego.

Uwzględnieniu funkcji przestrzennej konfiguracji wału przegubowego w modelowaniu dynamiki układu napędowego poświęcono miejsce w p. 11.3.

10.2.4. Podsumowanie p. 10.2.

W budowie układów transmisji momentu trakcyjnego należy dążyć do stosowania sprzęgieł równobieżnych.

Przy zastosowaniu (w wałach przegubowych) sprzęgieł nierównobieżnych należy dążyć do płaskiej konfiguracji wału.

Przy zastosowaniu sprzęgieł nierównobieżnych w płaskich układach konfiguracji wałów przegubowych należy dążyć do zapewnienia jednakowych wartości kątów załamania osi odcinków wałów w obydwóch sprzęgłach.

Przy zastosowaniu w płaskich wałach przegubowych sprzęgieł nierównobieżnych o jednakowych kątach załamania osi należy zapewnić odpowiedni dobór względnych kątowych położeń obydwóch sprzęgieł (przykład: - konfiguracja "A" według rysunku 8.69).

Włączenie funkcji przestrzennej konfiguracji wału przegubowego do procesu modelowania dynamiki układu napędu pojazdu szynowego zaprezentowano na przykładzie zamieszczonym w p. 11.4.

334

---