LABORATORIUM FIZYKI |
Ćwiczenie nr 1 |
|||
Wydział Inżynierii Lądowej |
Grupa nr 3 |
Zespół nr 3 |
Data
|
|
Nazwisko i imię: Grzywacz Wojciech |
Ocena: |
|||
Temat ćwiczenia: Wyznaczanie wartości przyspieszenia ziemskiego na podstawie pomiaru okresu drgań wahadła matematycznego. |
|
|||
|
Podpis: |
|||
Prowadzący: |
|
|
||
Wstęp
Doświadczenie ma na celu wyznaczenie wartości przyspieszenia ziemskiego.
Przyspieszenie ziemskie (g) jest to przyspieszenie grawitacyjne ciał swobodnie spadających na Ziemię, bez oporów ruchu. Z prawa powszechnej grawitacji Newtona można wyliczyć, że na powierzchni Ziemi jego wartość określa wzór:
![]()
gdzie G jest stałą grawitacji, MZ i RZ są odpowiednio masą i promieniem Ziemi. Możemy zauważyć ze przyspieszanie ziemskie zależy od odległości od środka Ziemi. Na biegunach, gdzie promień naszej planety jest najmniejszy, będzie ono miało największą wartość. Zmiana wartości przyspieszenia g wraz z szerokością geograficzną jest nie tylko wynikiem kształtu ziemi. Na wartość przyspieszenia wpływa również ruch obrotowy Ziemi - związane z nim przyspieszenie odśrodkowe zmniejsza mierzone przyspieszenie ziemskie na wszystkich szerokościach geograficznych poza biegunami. Oczywiście wartość przyspieszenia ziemskiego maleje wraz z wysokością nad powierzchnią Ziemi.
Metoda pomiaru
Za pomocą wahadła matematycznego postaramy się wyznaczyć przybliżoną wartość g. W tym celu dokonamy pomiaru okresu drgań wahadła i sprawdzimy zależność okresu drgań od jego długości. Wahadło matematyczne to punkt materialny zawieszony na nierozciągliwej i nieważkiej nici, (oczywiście jest to idealizacja wahadła matematycznego), całość umieszczona jest w polu sił ciężkości. Wahadło matematyczne o długości l ma to do siebie, że jeżeli zostanie odchylone od pionu o pewny kąt (tu przyjmujemy φ < 5º) i puszczone swobodnie, to zacznie wykonywać drgania harmoniczne.
Okres T drgań wahadła wyraża się wzorem:
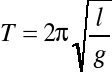
Po przekształceniu wzoru otrzymujemy:
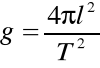
W ten sposób łatwo można zauważyć, że jeżeli zmierzymy okres drgań wahadła i jego długość to po podstawieniu do wzoru, otrzymamy przyspieszenie ziemskie g.
Układ pomiarowy
Badane wahadło to kulka metalowa, która zawieszona jest na cienkiej nici, która jest przymocowana do wysięgnika, który z kolei zamontowany jest w ścianie. Nie dysponuje profesjonalnym układem pomiarowym, dlatego też do celów pomiarowych posłużę się stoperem, który mierzy czas z dokładnością do 0,2 s. Stoper włączamy przy pierwszym puszczeniu kulki z punktu wychylenia i wyłączamy, gdy metalowa kulka wykona 10 pełnych drgań. Do zmierzenia długości wahadła użyliśmy dwóch przyrządów. Długość linki od punktu zaczepienia do kulki wyznaczyliśmy posługując się taśmą mierniczą, która pozwala mierzyć z dokładnością do 1 mm. Do zmierzenia średnicy kulki użyliśmy suwmiarki, której dokładność wynosi 0,1 mm.
4. Wykonanie ćwiczenia
Wychylenie wahadła od pionu, gdzie kąt wychylenia (φ) jest mniejszy od 5º (φ<5º).
Puszcze kulki oraz jednoczesne włączenie stopera.
Zmierzenie 10 drgań wahadła matematycznego.
Zapisanie wyników pomiaru.
Powtórzenie pomiaru jeszcze 9 razy.
Następnie zmierzyliśmy długość nici wykorzystując w tym celu taśmę mierniczą (długość nici od punktu zaczepienia do kulki) - 5 pomiarów. Zmierzyliśmy średnicę kulki, wykorzystując do tego suwmiarkę - 5 pomiarów.
5. Wyniki i ich opracowanie
Tabela 1. Wyniki pomiarów okresu drgań.
Numer pomiaru |
10T [s] |
1 |
20,3 |
2 |
21,0 |
3 |
20,8 |
4 |
21,0 |
5 |
20,8 |
6 |
21,0 |
7 |
19,0 |
8 |
20,4 |
9 |
21,2 |
10 |
21,4 |
Dokładność pomiaru czasu ΔT=0,1 [s]
Wartością najbardziej zbliżoną jest wartość średnia:
10![]()
10Tśr=20,69 [s]
Tśr=2,069 [s]
Tabela 2. Wyniki pomiarów długości wahadła matematycznego.
Numer pomiaru |
l [cm] |
d [mm] |
1 |
108,4 |
19,1 |
2 |
108,5 |
19,1 |
3 |
108,2 |
19,2 |
4 |
108,6 |
19,1 |
5 |
109,5 |
19,0 |
Dokładność pomiaru długości nici wynosi Δl=1[mm], a pomiaru średnicy kulki Δd=0,1[mm].
Wartością najbardziej zbliżoną jest wartość średnia. Postępujemy tak samo jak w przypadku liczenia średniej wartości okresu drgań, zatem:
lśr=108,64 [cm] dśr=19,10[mm]=1,91[cm]
Toteż całkowitą długość wahadła oznaczmy poprzez w,
wśr= lśr + 0,5 dśr=108,640+0,955=109,595[cm]=1,09595[m]
Wartość przyspieszenia ziemskiego:
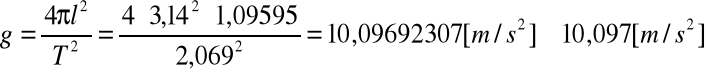
Rachunek błędów
Obliczenie odchyleń standardowych 10T, l, d:
1) 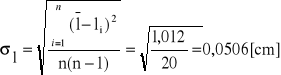
2) 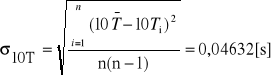
3) 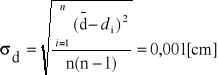
n - liczba pomiarów
Obliczanie niepewności przypadkowych (korzystając z tabeli studenta Fishera dla poziomu nieufności α=0,68):
Wykonano 5 pomiarów d i l. Odpowiadający takiej liczbie pomiarów i stopniowi ufności 0,68 wsp. Studenta - Fischera wynosi:
![]()
zatem:
![]()
![]()
Wartość 10T została zmierzona 10 razy - odpowiadający wsp. Studenta - Fischera :
![]()
![]()
Niepewności systematyczne
Pomiar długości nici l wykonywany był taśmą mierniczą o najmniejszej działce = 1mm więc jako niepewność systematyczną tego pomiaru przyjmujemy połowę tej działki czyli:
Δl=0,05[cm]
Z kolei pomiar średnicy kulki wykonywany był suwmiarką o podziałce = 0,1mm czyli jako niepewność systematyczną tego pomiaru przyjmujemy:
Δd=0,05[mm]
Czas 10T mierzony był stoperem o podziałce 0,2s więc:
Δ10T=0,1[s]
Obliczenie niepewności całkowitych d, l, T
Niepewności pomiarowe całkowite są sumą niepewności przypadkowych i systematycznych:
Δlc=0,028[cm]+0,05[cm]=0,078[cm]
Δdc=0,000[cm]+0,005[cm]=0,005[cm]
Δ10Tc=0,016[s]+0,1[s]=0,116[s]
a ponieważ:
![]()
więc:
ΔTc=0,0116[s]
Obliczenie g i błędu pomiarowego Δg
Ponieważ długość wahadła L powinniśmy mierzyć od punktu zaczepienia do środka kulki więc wzór na rzeczywistą wartość L ma postać:
![]()
a błąd pomiarowy przy jej wyznaczaniu:
![]()
Maksymalna niepewność względna określona wzorem (1) ma postać:
![]()
a dla danych zadania maksymalna niepewność względna wynosi:
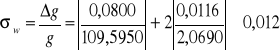
niepewność procentowa:
![]()
1,2%
niepewność maksymalna:
![]()
więc wynikiem doświadczenia jest otrzymana stała g równa:
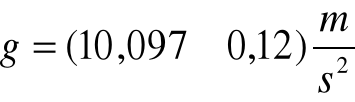
7. Wnioski
g zmierzone i wyliczone z ćwiczenia:
![]()
g z tablic fizycznych (dla Krakowa):
![]()
różnica wynosi: ![]()
Tak więc, po porównaniu wartości przyspieszenia ziemskiego zmierzonej w laboratorium i przeze mnie obliczonej, z wartością g z tablic fizycznych, widać, że odchylenie od wartości tablicowej wynosi :
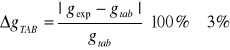
Wartość rzeczywista nie mieści się w oszacowanym maksymalnym błędzie pomiarowym.
Odchylenie od wartości tablicowej jest spowodowane :
przyjęciem że ruch wahadła jest ruchem harmonicznym
małą liczbą pomiarów długości nici (tylko 5)
jej rozciągliwością
zaniedbaniem oporu powietrza i masy nici
zaniedbaniem tarcia nici w punkcie zawieszenia kulki
zaniedbaniem rozmiarów kulki i traktowanie jej jako punktu materialnego (bez uwzględnienia jej momentu bezwładności)
nie uwzględnieniem faktu, że ruch nie odbywa się dokładnie w jednej płaszczyźnie
niedokładnością przyrządów pomiarowych lub osób posługujących się nimi.
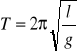
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Ćwicz. 71, Studia, 1 rok, od Magdy, FIZYKA, Fizyka, Laborki z fizyki, moje laborki
moja 13, 3 semestr, laborki z fizyki skał i gruntów, com miał
Laborka z fizyki
gęstość i wilgotność(1), 3 semestr, laborki z fizyki skał i gruntów, com miał
izotopy spr, Polibuda, Fiza, Fizyka sprawozdania (burdel jak cholera), Sprawozdania z Fizyki, labork
Ćwicz. 72, Studia, 1 rok, od Magdy, FIZYKA, Fizyka, Laborki z fizyki, moje laborki
wyznaczanie lepkości powietrza, laborki z fizyki
prom. kos. poprawione, Polibuda, Fiza, Fizyka sprawozdania (burdel jak cholera), Sprawozdania z Fizy
Oznaczenie kąta tarcia wewnętrznego i spójności w próbie trójosiowego ściskania(10), 3 semestr, labo
do wydruku, 3 semestr, laborki z fizyki skał i gruntów, com miał
Oznaczenie współczynnika filtracji skał, 3 semestr, laborki z fizyki skał i gruntów, com miał
budo2, 3 semestr, laborki z fizyki skał i gruntów
10(tabele), 3 semestr, laborki z fizyki skał i gruntów, com miał
Laborki z Fizyki- Sprawozdanie z siatki dyfrakcyjnej, Fizyka - LAB
Oznaczenie współczynnika filtracji skał(4), 3 semestr, laborki z fizyki skał i gruntów, fizyka skał
więcej podobnych podstron