rok akad. 2000/2001	Laboratorium z fizyki
nr ćwicz. 71	Promieniowanie cieplne
wydział: W.B. i I.Ś. kierunek: Budownictwo grupa: 1J	Ireneusz Tackowiak
data wykonania ćwiczenia	OCENA		data zal. ćwiczenia	podpis
08.04.2001 r	teoria:
		sprawozdanie:

1. ZASADA POMIARU.

W promieniowaniu cieplnym zdolność emisyjna promieniowania R_λ ciał rzeczywistych jest mniejsza od odpowiedniej wartości R_λc dla ciała doskonale czarnego. Dla każdego ciała prawdziwe jest prawo Kirchhoffa, które można zapisać:

R_λ (λ,T) = a_λ (λ,T) * R_λc (λ,T)

gdzie: aλ (λ,T) - współczynnik pochłaniania ciała.

Prawo Kirchhoffa stosuje się nie tylko do widmowej zdolności emisyjnej promieniowania Rλ, lecz również do emisji energetycznej ciała R. Emisja ta musi być równa mocy P wypromieniowanej przez jednostkę powierzchni ciała R = P (S) (dla ciała doskonale czarnego R_c = P (S) .

Uwzględniając prawo Stefana - Boltzmana:

R = δT4

gdzie:
T - temp. ciała

Otrzymamy: P = a S δ T⁴ (a = 1 - dla ciała doskonale czarnego)

Jeżeli temp. otoczenia T_O jest niższa od temp. ciała T, to ciało wypromieniowuje moc:

P = a S δ ( T⁴ - T_O⁴ )

W doświadczeniu porównuje się moc P wypromieniowaną przez badane ciało z mocą Po, wypromieniowaną w takich samych warunkach przez sadzę ( dla której a = 1). Wypromieniowana moc absorbowana jest przez termoparę „2” (schemat pomiarowy), wytwarzając w jej obwodzie prąd elektryczny o mocy P_I proporcjonalnej do P.

Ponieważ P_I = U² / R (R- wartość oporu obwodu),

musi zachodzić: P = f U2 (f- współczynnik proporcjonalności).

Wobec tego zgodnie z P = a S δ ( T⁴ - T_O⁴ ), przy tej samej temp. T badanego ciała i sadzy, znajdujących się w tych samych warunkach zew. opisanych przez temp. T_O zachodzi:

oraz

Dzieląc stronami otrzymamy:

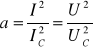
Równanie to pozwala obliczyć współczynnik pochłaniania „a” materiału, z którego wykonane jest dno naczynia „2” (schemat), ze stosunku napięć w obwodach termopary (U- napięcie w obwodzie termopary jeżeli ustawione jest nad nią badane ciało, U_C- napięcie jeżeli nad termoparą znajduje się ciało, którego powierzchnia jest poczerniona sadzą). Powierzchnie obu ciał są sobie równe,

a także jest jednakowa ich temperatura, gdyż w biegu wodnym połączone są szeregowo.

2. SCHEMAT POMIAROWY.

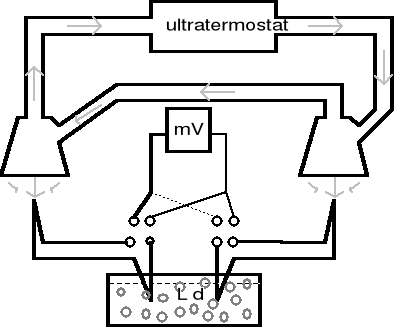
3. OCENA DOKŁADNOŚCI POJEDYNCZYCH POMIARÓW.

• Pomiar temperatury - termometr o dokładności 0,1C - podziałka termometru była bardzo mała, dlatego też względu na obecność obu laborantów i niedokładność ludzkiego oka można przyjąć dokładność w granicach dwóch działek - czyli 0,2C

• Pomiar napięcia - zarówno dla ciała badanego jak i dla sadzy wykonywany tym samym woltomierzem z odczytem cyfrowym , ze względu na duże wahania przyjmujemy dokładność 10 μV

4. TABELA POMIAROWA.

t [°C]	U [μV]	UC [μV]	a -	│aśr - ai│ -
60	111	171	0,421	0,09
65	158	220	0.515	0,004
70	181	247	0,536	0,025
75	205	280	0,536	0,025
80	210	300	0,49	0,021
85	250	342	0,534	0,023
90	286	387	0,546	0,036
wartość	średnia	=	aśr = 0,511	(∆a)p = 0,032

5. PRZYKŁADOWE OBLICZENIA.

Pomiar nr 1:

T = 60C

U₁ = 111 V

Uc₁= 171 V

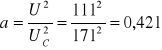
6. RACHUNEK BŁĘDÓW.

a) Błąd logarytmiczny dla pomiaru nr 1:

Błąd współczynnika a obliczono metodą różniczki logarytmicznej ze wzoru:

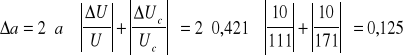
b) Błąd przeciętny:

Błąd przeciętny a podany obliczono ze wzoru:

Wartość średnia:

Błąd przeciętny: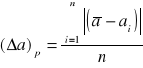

Błąd przeciętny pomiarów wynosi: 0,032

Błąd obliczony przy pomocy pochodnej logarytmicznej dla pomiaru nr 1 wynosi: 0,125

0,032 < 0,125

7. WNIOSKI I ZESTAWIENIE WYNIKÓW.

Jak widać z wyników otrzymanych w tabeli błąd przeciętny pomiaru nie jest duży i wynosi 0,032, jednak nie ma sensu podawanie takiego błędu w zestawieniu wyników, gdyż nie jest to błąd rzeczywisty. Dopiero uwzględnienie błędu aparaturowego (liczonego metodą pochodnej logarytmicznej), który jest znacznie większy niż błąd przeciętny pozwoli nam poznać rzeczywisty wynik doświadczenia. Wynik jest zgodny z zasadami teorii promieniowania termicznego, gdyż żadne ciało rzeczywiste nie może mieć stałej emisji większej od stałej emisji ciała doskonale czarnego, równej jedności.

a = 0,511 ± 0,125

---