Rok akademicki 2003/2004	LABORATORIUM Z FIZYKI
Nr ćwiczenia: 63	Procesy fizyczne w lampach Elektronowych.
Wydział: W.B. i I.Ś. Grupa: 2.3 6 lab	Robert Wachowski
Data wykonania: 30.10.2003 r.	OCENA		Data zaliczenia	Podpis
	Teoria
	Sprawozdanie

1. ZASADY POMIARU

Prąd elektryczny może płynąć także bez udziału przewodzącego materiału np. w lampach elektronowych. W częściach metalowych obwodu z lampą elektronową prąd polega na ruchu swobodnych elektronów w kierunku przeciwnym do umownego kierunku prądu. By obwód był zamknięty, w przerwie między anodą i katodą muszą też płynąć elektrony w kierunku od katody do anody. Rozgrzana katoda wysyła więc swobodne elektrony tworzące prąd anodowy. Zjawisko to nosi nazwę termoemisji. Ponieważ elektrony mogą się swobodnie poruszać tylko wewnątrz metalu od wyjścia na zewnątrz są powstrzymywane siłami przyciągania jonów dodatnich metalu. Na granicy metal-powietrze istnieje więc nagła zmiana potencjału zwana barierą potencjału. By elektron mógł się z metalu wydostać, musi pokonać tę barierę, tzn. musimy mu dostarczyć pracy równej przyrostowi energii potencjalnej przy przejściu z metalu do próżni. Jeśli skok potencjału na granicy zetknięcia przewodnika z powietrzem wynosi U , praca będzie równa eU. Nazywamy ją pracą wyjścia elektronu z metalu. Jeśli wszystkie elektrony tworzące prąd w lampie elektronowej docierają do anody to mamy do czynienia z prądem nasycenia.

Doświadczenia wykazują iż gęstość prądu nasycenia j_n wzrasta bardzo szybko wraz ze zwiększeniem temperatury katody. Na podstawie teorii kwantowej opisującej zjawisko termoemisji można obliczyć wartość gęstości prądu nasycenia. Wyraża ją wzór Richardsona - Dushmana :

gdzie:

T - temperatura bezwzględna w K,

W - praca wyjścia,

k - stała Boltzmana,

B - stała emisyjna zależna od stanu powierzchni metalu i stopnia jego czystości,

j_n - gęstość prądu nasycenia, j_n =

I_n - natężenie prądu nasycenia,

S_k - powierzchnia katody.

Logarytmując wzór Richardsona - Duchmana i dokonując uproszczeń, uzyskujemy:

=

Wykresem powyższej zależności w układzie współrzędnych ln j_n i 1/T jest linia prosta, zwana prostą Richardsona:

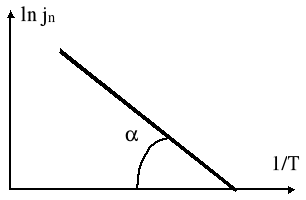
Rys. 1. Prosta Richardsona.

Z wykresu i w oparciu o wzór możemy wyznaczyć pracę wyjścia ”W”:

2. SCHEMAT UKŁADU POMIAROWEGO

Rys. 2. Schemat układu pomiarowego

3. OCENA DOKŁADNOŚĆI POJEDYŃCZYCH POMIARÓW

Dokładność pomiarów wynika z klasy przyrządu pomiarowego podanej przez producenta.

• woltomierz analogowy klasy 0,5

• miliamperomierz klasy 0,5

• amperomierz cyfrowy

ΔI_ż = ± 0,3% rdg + 1 mA

4. TABELE POMIAROWE

Tab. 1. Wyniki pomiarów

Lp.	Ua = 150 V
		Iż ± Δ Iż	Uż ± Δ Uż	In ± Δ In
		[A]	[V]	[mA]
1.	0,54 ± 0,003	1,09 ± 0,015	0,05 ± 0,04
2.	0,56 ± 0,003	1,20 ± 0,015	0,20 ± 0,04
3.	0,58 ± 0,003	1,30 ± 0,015	0,50 ± 0,04
4.	0,60 ± 0,003	1,40 ± 0,015	0,95 ± 0,04
5.	0,62 ± 0,003	1,48 ± 0,015	1,60 ± 0,04
6.	0,64 ± 0,003	1,57 ± 0,015	2,80 ± 0,04
7.	0,66 ± 0,003	1,66 ± 0,015	4,60 ± 0,04
8.	0,68 ± 0,003	1,75 ± 0,015	7,00 ± 0,04
9.	0,70 ± 0,003	1,90 ± 0,015	12,0 ± 0,15
10.	0,72 ± 0,003	1,95 ± 0,015	16,0 ± 0,15
11.	0,74 ± 0,003	2,05 ± 0,015	22,5 ± 0,15
12.	0,76 ± 0,003	2,16 ± 0,015	30,0 ± 0,15

Tab. 2. Wyniki obliczeń

Lp.	Pż ± Δ Pż	T	± Δ		jn	ln jn
		[W]	[K]	[K^-1]
1.	0,59 ± 0,01	675,0	0,001481	± 0,0000073	0,05	-3,00
2.	0,67 ± 0,01	697,8	0,001433	± 0,0000065	0,2	-1,61
3.	0,75 ± 0,01	718,1	0,001393	± 0,0000059	0,5	-0,69
4.	0,84 ± 0,01	737,8	0,001355	± 0,0000054	0,95	-0,05
5.	0,92 ± 0,01	754,3	0,001326	± 0,0000050	1,6	0,47
6.	1,00 ± 0,01	771,6	0,001296	± 0,0000047	2,8	1,03
7.	1,10 ± 0,01	788,5	0,001268	± 0,0000044	4,6	1,53
8.	1,19 ± 0,02	804,9	0,001242	± 0,0000041	7	1,95
9.	1,33 ± 0,02	827,6	0,001208	± 0,0000037	12	2,48
10.	1,40 ± 0,02	838,9	0,001192	± 0,0000036	16	2,77
11.	1,52 ± 0,02	855,3	0,001169	± 0,0000034	22,5	3,11
12.	1,64 ± 0,02	872,3	0,001146	± 0,0000032	30	3,40

5. PRZYKŁADOWE OBLICZENIA WYNIKÓW

Moc właściwa katody, czyli moc żarzenia przypadająca na jednostkę powierzchni katody obliczamy ze wzoru:

P_ż =

gdzie:

P_ż - moc właściwa katody

I_ż - prąd żarzenia

S_k - powierzchnia katody, przyjęliśmy dla AZ-1: S_k = 1 cm²

Np. dla pomiaru nr 7 :

P_ż =
= 1,10W

Temperaturę katody wyznaczyliśmy ze wzoru:

T =

gdzie:

P_ż - moc właściwa katody

σ - stała = 5,67 × 10^-12

ε - emisyjność całkowita równa 0,5 dla katody lampy AZ-1

Np. dla pomiaru nr 7 :

T =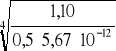
= 788,5 K

Przykładowe obliczenie wartości
dla pomiaru nr 7:

=
= 0,001268 K^-1

Gęstość prądu nasycenia obliczyliśmy ze wzoru:

j_n =

gdzie:

j_n - gęstość prądu nasycenia

I_n - natężenie prądu nasycenia

S_k - powierzchnia katody, przyjęliśmy dla AZ-1: S_k = 1 cm²

Np. dla pomiaru nr 7 :

j_n =
= 4,60

Przykładowe obliczenie wartości ln j_n dla pomiaru nr 7:

ln 4,60 = 1,53

6. RACHUNEK BŁĘDÓW

Błąd ΔP_ż (mocy właściwej katody) obliczyliśmy ze wzoru:

ΔP_ż = P_ż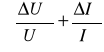

Błąd Δ
obliczyliśmy ze wzoru:

Δ
=

Wyniki błędów dla poszczególnych odczytów zestawiono w tabelach.

7. ZESTAWIENIE WYNIKÓW

Wykresy j_n = f (I_ż), j_n = f (P_ż), ln j_n = f (1/T) przedstawiono na następnych stronach.

W oparciu o wykres zależności ln j_n = f (1/T) i wzór

W = k × tg α (gdzie k - stała Boltzmana = 1,38 × 10^-23
)

możemy wyznaczyć pracę wyjścia elektronu z katody lampy AZ-1.

Z funkcji trygonometrycznej możemy obliczyć tg α.

tg α =
= 16964,29 K

Po podstawieniu na pracę wyjścia:

W = 1,38 × 10^-23 × 16964,29 K = 2,34107× 10^-19 J

Wiedząc, że: 1J = 6,242 × 10¹⁸ eV mamy:

W = 1,46 eV

8. UWAGI I WNIOSKI

Przeprowadzone doświadczenie miało na celu wyznaczenie pracy wyjścia elektronów, metodą prostej Richardsona. Jak wiadomo, praca wyjścia jest różna dla różnych ciał (1,8 eV dla litu lub 4,7 eV dla złota).

Należało znaleźć (z danego wykresu) współczynnik kierunkowy prostej, a następnie obliczyć pracę wyjścia (znając stałą Boltzmanna i tg kąta).

Na błędy pomiarów wpłynęła przede wszystkim niedokładność wykonywanych odczytów, różne czasy pomiędzy kolejnymi odczytami.

Praca wyjścia elektronów dla badanego wolframu wynosi: W=1,46 eV.

Dostałem za taki jak jest 4,0

Nie zaznaczyłem na wykresie ln j_n = f (1/T) błędów.

2

8

--

+

+

--

I_n

U_ż

I_ż

mA

A

V

Zasilacz anodowy

ZS - 1

Zasilacz

ZT-98-3M

---