I MDB 2005-04-29

BANAK MARCIN

Sprawozdanie z ćwiczenia nr 1.x

Temat: WYZNACZANIE PRZYŚPIESZENIA ZIEMSKIEGO ZA

POMOCĄ WAHADŁA REWERSYJNEGO.

Zagadnienia teoretyczne.

Newtonowskie prawo powszechnego ciążenia stwierdza, że wszelkie ciała oddziaływują ze sobą wzajemnie siłą przyciągania skierowaną wzdłuż prostej łączącej środki mas obu ciał i mającą wartość:

F= γ ⋅
,gdzie: M₁ , M₂ - masy oddziaływujących ciał

R - odległość między środkami mas

• stała grawitacyjna

γ = 6,67⋅10

Ciężar to siła, która nadaje ciałom przyśpieszenie ziemskie:

Q = m* g

Gdzie: Q - ciężar ciała

m - masa ciała

g - wektor przyśpieszenia ziemskiego

g ≈ 9,81

Ruch drgający harmoniczny prosty to ruch, w którym następuje okresowa zmienność określonej wielkości fizycznej np. przemieszczenia x.

F = - k ⋅ x gdzie: k - współczynnik proporcjonalności

m
= - k ⋅ x

+ ⋅ x = 0

x = A cos (w t + γ )  - część koła

 =

 =

x = A cos [  ( t + ) + δ ] = A cos ( t + 2 + δ ) = A cos ( t + δ )

T = = 2
T - okres drgań

Wahadło matematyczne jest to wyidealizowane ciało o punktowej masie zawieszone na cienkiej, nierozciągliwej i nieważkiej nici.

l - długość nici

N - naprężenie

γ - kąt odchylenia nici od pionu

Wahadło fizyczne jest to dowolne ciało sztywne mogące obracać się w poziomej osi nie przechodzącej przez środek jego masy. Zgodnie z okresem drgań wahadła fizycznego dla małych wychyleń można obliczyć według wzoru:

a - odległość punktu A od środka masy

b - odległość punktu B od środka masy

C - środek ciężkości

Jeśli oś obrotu przechodzi przez punkt A to okres drgań wahadła fizycznego względem tego punkt ma wzór: T_A = 2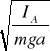
gdzie: I_A - moment bezwładności

I_A = I₀ + ma gdzie: I - moment bezwładności względem osi

przechodzącej przez środek masy

T_A = 2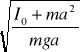

T_B = 2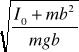

T_A = T_B

2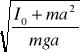
= 2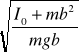

I₀ (a - b) = mab (a - b) gdy a  b I ₀ = mab

T_A = T_B = 2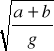
l _zr = a + b mamy zatem : T_A = T_B = 2

Wyznaczając ten okres drgań i mierząc odległość między ostrzami O1 i O2 równą odległości zredukowanej wahadła rewersyjnego l możemy obliczyć przyśpieszenie ziemskie ze wzoru:

g =

Przebieg ćwiczenia.

• Wyznaczamy odległość między ostrzami
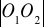
  = l

• Zawieszamy wahadło na ostrzu O₁ i ustawiamy masę m₂ w punkcie A

• Przesuwając masę m od A do B co 5 cm. mierzymy dla kolejnych jej położeń l_i okresy drgań T_i . W tym celu mierzymy czas t _i , np. n =10 wahnięć i obliczamy czas jednego wahnięcia ze wzoru:

T_i =

Wyniki zamieszczamy w tabelce.

• Zawieszamy wahadło na ostrzu O₂ i przesuwając masę m₂ od B do A i powtarzamy czynności jak w poprzednim punkcie

TABELA

Lp.	Lzr [m]	Li [m]	T1i [s]	T2i [s]	T [s]	g [m/s²]
1.	1,30	1,30	2,40	2,30	2,1	11,647±1,109
2.	1,30	1,25	2,30	2,25	2,1
3.	1,30	1,20	2,25	2,20	2,1
4.	1,30	1,15	2,20	2,20	2,1
5.	1,30	1,10	2,10	2,15	2,1
6.	1,30	1,05	2,15	2,10	2,1
7.	1,30	1,00	2,10	2,15	2,1
8.	1,30	0,95	2,05	2,15	2,1
9.	1,30	0,90	2,00	2,10	2,1
10.	1,30	0,85	2,00	2,10	2,1
11.	1,30	0,80	2,00	2,00	2,1
12.	1,30	0,75	1,85	2,00	2,1
13.	1,30	0,70	1,80	1,90	2,1
14.	1,30	0,65	1,85	2,00	2,1
15.	1,30	0,60	1,80	2,10	2,1
	,	,	,	,	,
	,	,	,	,	,
	,	,	,	,	,
	,	,	,	,	,
	,	,	,	,	,

ΔL=0,01 [m]

OBLICZENIA:



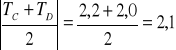
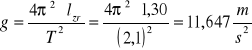
Obliczanie błędu:

Δ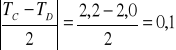
[s]

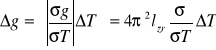
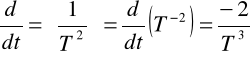
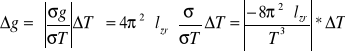
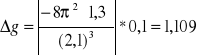
m/s²]

WNIOSKI:

Przyśpieszenie ziemskie g=9,81
.W wykonanym ćwiczeniu g=11,647
. Na niedokładności wyniku zsumowały się niedoładności pomiaru czasu wahnięć wahadła rewersyjnego oraz niedokładności pomiaru odległości przesuwamych mas

1

4

---