1. PODSTAWOWE POJĘCIA STATYSTYCZNE

Zbiory dowolnych elementów (osób, przedmiotów, faktów) podobnych ale nie identycznych - pod względem określonych właściwości i poddanych badaniom statystycznym określa się mianem zbiorowości (populacji statystycznych). Elementy składowe zbiorowości poddane bezpośredniej obserwacji lub pomiarowi noszą nazwę jednostek statystycznych lub jednostek badania. Zbiorowości statystyczne powinny być ściśle określone pod względem rzeczowym (kto lub co jest przedmiotem badania), przestrzennym (gdzie znajduje się zbiorowość) oraz czasowym (jakiego momentu dotyczy badanie lub okresu dotyczy badanie).jeśli przedmiotem badania są wszystkie jednostki statystyczne, co do których chcemy formułować ogólne wnioski - to zbiorowość tę nazywamy zbiorowością (populacją ) generalną. Podzbiór populacji generalnej, obejmujący część jej elementów wybranych w określony sposób - nosi nazwę zbiorowości próbnej (próby). Próba podlega badaniu statystycznemu, którego wyniki są uogólniane na całą zbiorowość generalną. W praktyce badań statystycznych bardzo często nie można badać całej zbiorowości generalnej, a chcąc zbadać interesujące nas właściwości pobieramy skończona liczbę elementów i poddajemy je obserwacji. Aby uzyskane wyniki można było odnieść do zbiorowości generalnej próba musi być reprezentatywna. Reprezentatywność próby zależy od : sposobu doboru próby (losowy, celowy), liczebności próby. Jeżeli próba została wybrana w sposób losowy i jest dostatecznie liczna to próba jest reprezentatywna. Badaniu statystycznemu podlegają właściwości jednostek statystycznych. Są one określane mianem cech statystycznych. Cechy mierzalne (ilościowe), cechy niemierzalne (jakościowe).

Pomiar polega na przyporządkowaniu cechom statystycznym określonych symboli, którymi mogą być: liczby, litery alfabetu, formy geometryczne, kolory, opis słowny itp. W statystyce cechom statystycznym najczęściej przyporządkowuje się liczby które powinny możliwie wiernie odzwierciedlać mierzoną cechę. Pomiar bezpośredni - to taki pomiar który jest jednoznacznie określony i wyrażony w odpowiednich jednostkach np. ciężar w gramach, temperatura w stopniach.. w naukach społecznych problem pomiaru jest bardziej skomplikowany niż w naukach eksperymentalnych. Wyróżnia się tu różne poziomy pomiarów, którym odpowiadają określone skale pomiarowe. Czynność odwzorowywania mierzonej cechy za pomocą wybranej skali nazywamy skalowaniem. Stevens wyróżnił cztery skale pomiarowe: nominalna, porządkową (rangową), przedziałową (ilorazową) oraz stosunkową (ilorazową). Dwie pierwsze z nich zaliczane są do skal niemetrycznych (jakościowych), pozostałe zaś do skal metrycznych (ilościowych).

Skala nominalna - stanowi najmniej precyzyjny sposób pomiaru. Liczby pełnią tu jedynie rolę umownych symboli służących do identyfikacji jednostek statystycznych i ich klasyfikacji do wyróżnionych kategorii. Jedyną dopuszczalną operacja matematyczną na danych typu nominalnego jest zliczanie jednostek należących do określonej kategorii danej cechy i obliczanie na tej podstawie np. proporcji, odsetek. Przykładowo wynik pomiarów jednostek pod względem cechy jakościowej płeć można przedstawić w postaci dwudzielnej (dychotomicznej ) skali nominalnej (kobieta, mężczyzna), a cechy grupa krwi - wielodzielnej (politomicznej) skali nominalnej (A, AB, B, 0 ). O poszczególnych wariantach cech można tylko powiedzieć że są równe lub różne.

Skala porządkowa (rangowa) - posiada wszystkie cechy skali nominalnej, a dodatkowo pozwala na porządkowanie jednostek w ramach wyróżnionych kategorii pod względem natężenia badanej cechy. Możliwe są zatem stwierdzenia nie tylko o równości czy różności elementów ale również określenia typu większy niż czy mniejszy niż. W skali rangowej liczby zwane rangami wyznaczają kolejność występowania jednostek, ale nie określają odległości między nimi. Można więc stwierdzić, że sok A jest słodszy od soku B ale nie można określić o ile. Porządkowanie jednostek według badanej cechy przy wykorzystaniu rang może być uporządkowaniem mocnym lub słabym. Uporządkowanie jest słabe jeżeli generowane jest przez relację typu mniejszy lub równy lub większy lub równy, natomiast mocne generowane jest przez relację typu mniejszy lub większy.

Skala przedziałowa (interwałowa) - zachowuje wszelkie własności skali rangowej, a oprócz tego umożliwia określenie odległości dystansu między jednostkami. W skali tej punkt zerowy ustalony jest umownie (brak zera absolutnego). Przykładowo w skali temperatury Celsjusza zero ustalone jest jako punkt w którym zamarza woda. Na liczbach w skali przedziałowej nie można wykonywać dzielenia.

Skala stosunkowa (ilorazowa) - ma własności trzech poprzednich skal, a jej cechą charakterystyczną jest posiadanie naturalnego punktu zerowego. Punkt ten oznacza fizyczny poziom zerowy) danej cechy. Umożliwia to dokonywanie na liczbach w tej skali wszystkich operacji matematycznych.

Skale pomiarowe - mają kumulatywny charakter tzn charakteryzują się narastającym stopniem dokładności pomiaru. Każda następna skala jest precyzyjniejsza od poprzedniej.

2. RODZAJE BADAŃ STATYSTYCZNYCH

Badania Pełne dotyczące przeprowadzane na całej populacji generalnej:

• spis,

• rejestracja bieżąca,

• sprawozdawczość.

Spisem statystycznym nazywamy jednorazowe lub powtarzalne co pewien czas badanie, odzwierciedlające szczegółowy stan danej zbiorowości statystycznej z punktu widzenia określonych cech. Np. narodowy spis powszechny przeprowadzany w Polsce co 10 lat. Rejestracja bieżąca polega na systematycznym notowaniu ściśle określonych zdarzeń, będących przedmiotem badania statystycznego.

Sprawozdawczość statystyczna polega na sporządzaniu przez jednostki sprawozdawcze sprawozdań na jednolitych formularzach.

Badania częściowe: reprezentacyjne, monograficzne, ankietowe.

Badanie reprezentacyjne polega na tym że z całej zbiorowości (populacji generalnej) pobiera się próbę, przeprowadza dokładne badanie jednostek wchodzących w jej skład, a następnie przenosi się wyniki badania na całą populację. Dobór jednostek do próby może być losowy jak i celowy. W doborze celowym subiektywnym wybór jednostek do próby uzależniony jest od osoby prowadzącej badanie. Metoda monograficzna - polega na wielostronnym opisie i szczegółowej analizie wybranej jednostki (województwa, gminy, przedsiębiorstwa) lub niewielkiego zespołu. Wybrana świadomie do badania jednostka powinna być typową lub wyróżniającą się (wzorzec).

Metoda ankietowa - jest badaniem opinii dotyczących określonego problemu lub zjawiska według ustalonego zestawu pytań. Stosując tą metodę badania nie prowadzi się bezpośrednich obserwacji, ale zawierający pytania kwestionariusz jest kierowany do wybranej grupy osób (ankietowanych respondentów). Badanie ankietowe może mieć charakter otwarty (np. redakcja pisma zwraca się do swoich czytelników o wyrażenie opinii na temat zamieszczonych w ni artykułów oraz ich autorów). Istotnym czynnikiem wpływającym na wyniki badań jest właściwe opracowanie kwestionariusza zawierającego pytania. Powinny być one tak skonstruowane, aby stwarzały możliwość ankietowanemu możliwość formułowania własnych opinii, wniosków i spostrzeżeń. Jedną z podstawowych zasad stosowanych w tego rodzaju badaniach jest zachowanie anonimowości respondentów.

W przypadku braku możliwości przeprowadzenia zarówno badania pełnego jak i częściowego stosuje się postępowanie nazwane szacunkiem statystycznym.

Szacunek statystyczny to postępowanie, w którym liczebność zbiorowości ustalana jest na podstawie informacji o innej zbiorowości logicznie powiązanej z badaną. Np. czas przeznaczony przez określona grupę ludzi na czytanie książek i czasopism można szacować na podstawie ilości zakupionych książek i czasopism.

Szczególnymi metodami szacunku statystycznego są rachunki interpolacyjne i ekstrapolacyjne. Interpolacja polega na szacowaniu nieznanych wartości badanej cechy na podstawie znajomości jej wcześniejszych i późniejszych realizacji. Ekstrapolacja pozwala na ustalenie nieznanych wartości znajdujących się poza przedziałem wartości znanych. Zarówno interpolacja jak i ekstrapolacja mogą mieć charakter liniowy lub nieliniowy. O liniowym charakterze rozwoju danego zjawiska mówimy wówczas gdy zmienia się ono w równych jednostkach czasu o tę samą wielkość absolutną. Jeśli natomiast badane zjawisko w równych odstępach czasu zmienia się o tę samą wielkość stosunkową (stopę wzrostu) - to mówimy o nieliniowym rozwoju.

3. ORGANIZACJA BADAŃ STATYSTYCZNYCH

Celem badania statystycznego jest realizacja jednego lub kilku wymienionych zadań:

• poznanie rozkładu zbiorowości pod względem wybranej lub wybranych cech (analiza struktury),

• ocena rodzajów związków występujących między cechami (analiza współzależności),

• poznanie zmian zbiorowości w czasie (analiza dynamiki).

Niezależnie od celu badania statystycznego, całość prac związanych z jego realizacją można podzielić na cztery etapy:

• przygotowanie (programowanie) badania,

• obserwację statystyczną,

• opracowanie i prezentację materiału statystycznego,

• opis lub wnioskowanie statystyczne.

Programowanie badania oznacza szczegółowo rozpisana koncepcję zamierzonego przedsięwzięcia. Etap ten obejmuje czynności przygotowawcze, takie jak ustalenie celu, przedmiotu i zakresu badania.

Obserwacją statystyczną nazywamy proces zbierania informacji (danych) statystycznych. Zbiór uzyskanych w wyniku obserwacji tworzy materiał statystyczny. Jeśli dane gromadzone są specjalnie dla celów badania statystycznego mówimy o materiale pierwotnym. Materiałem pierwotnym są np. dane zebrane podczas narodowego spisu powszechnego ludności. Służą one wyłącznie do realizacji programu statystycznego jakim jest spis. Źródłem pozyskania danych pierwotnych mogą być również wywiad lub ankieta. Dane zgromadzone z innych powodów np. do celów związanych z polityką podatkową lub dyscyplina pracy), a wykorzystywane w badaniach statystycznych tworzą wtórny materiał statystyczny.

Trzeci etap badania statystycznego - opracowanie i prezentacja materiału statystycznego obejmuje dwie zasadnicze części grupowanie i zliczanie. Grupowanie polega na wyodrębnianiu jednorodnych lub względnie jednorodnych części obejmujących jednostki o takich samych lub zbliżonych właściwościach. Wyróżnia się dwa podstawowe rodzaje grupowania: typologiczne i wariancyjne. Celem grupowania typologicznego (np. według cech przestrzennych, rzeczowych, czasowych) jest wyodrębnienie różnych jakościowo grup. Grupowanie wariancyjne opiera się na cesze ilościowej i polega na łączeniu w klasy jednostek statystycznych o takich samych lub zbliżonych wartościach cech. Czynnością ściśle związaną z grupowaniem jest zliczanie danych. Może ono odbywać się w rozmaity sposób: od zliczania ręcznego aż do wykorzystania komputerów.

Jeśli przedmiotem badania jest niewielka liczba jednostek statystycznych, to uporządkowany ciąg wartości badanej cechy tworzy szereg szczegółowy (wyliczający). Porządkowanie polega na ustawianiu cechy w kolejności rosnącej lub malejącej. Jeśli więc cech ta przyjmuje wartości x₁, x₂, x₃...x_n, to rosnące uporządkowanie można zapisać następująco x₁≤x₂≤x₃≤...≤x_n, a malejące x₁≥x₂≥x₃≥...≥x_n.

Szeregiem rozdzielczym nazywamy zbiór wartości liczbowych uporządkowanych według wariantów badanej cechy mierzalnej lub niemierzalnej przy czym poszczególnym wariantom zmiennej przyporządkowane są odpowiadające im liczebności. Zestawienie wyników w postaci szeregu rozdzielczego z cechą mierzalną nazywamy rozkładem empirycznym. Rozkład ten obrazuje strukturę badanej zbiorowości z punktu widzenia określonej cechy statystycznej.

Liczba przedziałów klas w szeregu uzależniona jest od obszaru zmienności badanej cechy (tj różnicy między maksymalna i minimalna wartością cechy), od liczebności zbiorowości oraz od celu badania. Im liczniejsza zbiorowość i większy obszar zmienności, tym więcej powinno być przedziałów.

Wzory za pomocą których można określić orientacyjna liczbę klas w zależności od liczebności zbiorowości.

k=1+3,322log n

k - liczba przedziałów klasowych

n - liczebność zbiorowości

Rozpiętość przedziału zwana interwałem lub rozstępem klasowym (przedziałowym), jest różnicą między górną i dolną granicą klasy. Jest ona uwarunkowana obszarem zmienności badanej cechy, a tym samym liczba ustalonych klas, stąd też przybliżona wielkość interwałów można wyznaczyć ze wzoru:

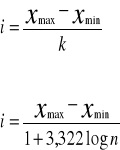
Przy budowie ilościowego szeregu rozdzielczego wyróżniamy trzy etapy:

• ustalenie liczby klas oraz wielkości przedziałów klasowych,

• przyporządkowanie danych przyjętym poszczególnym przedziałom klasowym

• zliczanie liczby jednostek w każdej klasie

Różnicę między x_1i a dolna x_0i granicą i - tego przedziału nazywamy rozpiętością przedziału klasowego. Przy grupowaniu z reguły staramy się ustalić jednakowe rozpiętości przedziałów klasowych. Przy równej rozpiętości przedziałów klasowych liczebności, częstości występujące w poszczególnych klasach są porównywalne. Jeżeli badana populacja jest niejednorodna i występuje duża koncentracja wartości w którejś z grup, wówczas należy stosować różne rozpiętości przedziałów klasowych. Dobór przedziałów klasowych powinien iść w tym kierunku aby szereg rozdzielczy dał możliwie szczegółowy, ale jednocześnie przejrzysty obraz struktury zbioru statystycznego. W odróżnieniu od dotychczas przedstawianych szeregów rozdzielczych (które nazywamy prostymi) wyróżniamy też szeregi skumulowane. Uzyskamy je z szeregów prostych przez dodanie kolejnych przedziałów klasowych i odpowiadających im liczebności. Przyporządkowanie kolejnym wartościom cechy statystycznej odpowiadających im częstości skumulowanych (lub liczebności skumulowanych) nazywamy dystrybuantą empiryczną.

Przykład

Badano czas reakcji organizmu osób cierpiących na pewne schorzenie po zażyciu nowego leku. Zbiorowość statystyczną stanowiło 150 pacjentów leczonych w szpitalu. Mierzono czas w (min) od podania jednorazowej dawki leku do momentu wystąpienia pewnego objawu. Zebrane wyniki przedstawiono w postaci prostego szeregu rozdzielczego jak i szeregu rozdzielczego kumulacyjnego.

Czas reakcji w min	Liczba osób	Liczebność skumulowana
3 - 7 8 - 12 13 - 17 18 - 22 23 - 27 28 - 32 33 - 37 38 - 42	3 4 15 24 70 22 7 5	3 7 22 46 116 138 145 150
Razem	150

Tablice wielodzielcze.

Szeregi rozdzielcze stosujemy dla grupowania prostego opartego na jednej cesze. W praktyce stosuje się także grupowanie oparte na kilku cechach. Tablice opisujące populacje wielocechowe noszą nazwę tablic wielodzielczych. Wśród tablic wielodzielczych na szczególna uwagę zasługują tablice dwudzielcze zwane korelacyjnymi.

Przykład

Z populacji mężczyzn urodzonych w 1970 r wybrano losowo grupę złożona z 90 osób i określono ich wagę i wzrost. Wagę mierzono z dokładnością do 0,1kg a wzrost 0,1cm. Otrzymane wyniki zaprezentowano w tablicy dwudzielnej.

waga	wzrost
Granice klas	Granice klas
		161,8-165,2	165,3-168,6	168,7-172	172,1-175,4	175,5-178,8	178,9-182,2	182,3-185,6
49-54	4	2	1	1			1
54,1-59	2	9	2			2
59,1-64	2	4	8	3	1
64,1-69			4	9	5	1	3
69,1-74	1	1			2	9	5
74,1-79		1	1				3
79,1-84				1		1	1

W szeregach rozdzielczych (punktowych i przedziałowych) do określania rozkładu czyli struktury badanej zbiorowości stosuje się obok liczebności bezwzględnych wskaźniki struktury. Wskaźnik struktury (zwany też częstością, liczebnością, frakcją lub odsetkiem ) jest ilorazem liczby jednostek o danej wartości cechy do liczebności całej zbiorowości statystycznej N. Wskaźniki struktury mogą być wyrażane w ułamku, procentach, promilach:

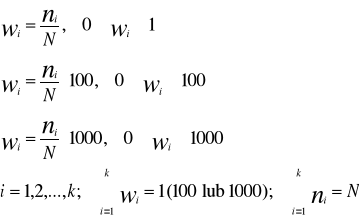
Przykład

W tabeli poniżej przedstawiono dwa szeregi rozdzielcze przedziałowe opisujące dwie zbiorowości (pracowników zakładów A i B) pod względem jednej cechy (wieku). Liczebności w tej tablicy podano zarówno w liczbach bezwzględnych (absolutnych) jaki i względnych (wskaźnikach struktury).

Wiek w latach	ZAKŁAD A		ZAKŁAD B
		Liczebności bezwzględne	Wskaźniki struktury (w %)	Liczebności bezwzględne	Wskaźniki struktury (w %)
18 - 24 25 - 34 35 - 44 45 - 54 55 - 59 60 - 65	204 264 356 320 201 48	14,64 18,95 25,56 22,97 14,43 3,45	274 355 472 429 271 68	14,66 18,99 25,25 22,95 14,50 3,65
Razem	1393	100	1869	100

Wskaźniki struktury pracowników zakładu A w poszczególnych grupach wieku obliczono następująco: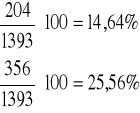

W analogiczny sposób obliczono wskaźniki struktury dla zbiorowości pracowników zakładu B.

Jak wynika z informacji zawartych w tabeli struktura obu załóg według wieku jest bardzo podobna, czego nie byłoby widać, gdyby ograniczono się tylko do liczb bezwzględnych.

Zestawienie wskaźników struktury dla dwóch lub więcej szeregów statystycznych pozwala na porównanie wewnętrznej budowy danej zbiorowości. Oceny podobieństwa porównywanych struktur można dokonać za pomocą względnego wskaźnika podobieństwa struktur,

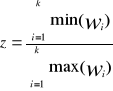
W liczniku tego wzoru znajduje się suma mniejszych wskaźników struktury zaobserwowanych w kolejnych przedziałach klasowych porównywanych rozkładów w mianowniku zaś suma wskaźników większych. Wskaźnik Z przyjmuje wartości z przedziału zamkniętego <0,1>, przy czym Z=1 świadczy o identyczności porównywanych struktur, zaś Z=0 informuje że są one zupełnie różne.

Obliczony w oparciu o dane z powyższej tabeli względny wskaźnik podobieństwa struktur przyjmuje wartość:

Do prezentacji materiału statystycznego wykorzystywane są również wykresy statystyczne. Wykres statystyczna - to wizualna forma prezentacji danych statystycznych oraz wyników analizy statystycznej. Z punktu widzenia form graficznych można wyróżnić następujące formy wykresów:

• liniowe w których prezentowane wielkości statystyczne są przedstawione w postaci pionowych lub poziomych odcinków, które są obrazem tych wielkości w odpowiedniej skali,

• powierzchniowe służące do prezentacji wielkości statystycznych za pomocą powierzchni figur płaskich (np. wykresy kołowe, słupkowe). Według kryterium rodzaju szeregu będącego przedmiotem prezentacji graficznej wyróżnia się między innymi następujące wykresy statystyczne: - wykresy obrazujące szeregi rozdzielcze (wykresy strukturalne),

• wykresy obrazujące szeregi przestrzenne (np. kartogramy),

• wykresy obrazujące szeregi czasowe (wykresy dynamiczne).

Dane statystyczne prezentowane w postaci szeregów rozdzielczych prezentowane są zwykle za pomocą:

• histogramów (wykresów słupkowych),

• diagramów (wieloboków liczebności)

• krzywych liczebności (częstości).

Jeśli przy sporządzaniu wykresów korzysta się z układu współrzędnych, to na osi odciętych odkłada się zazwyczaj wartości cechy, a na osi rzędnych liczebności (częstości występowania wariantów cech.

Histogram - to zbiór przylegających prostokątów, których podstawy - równe są interwałom klasowym - spoczywają na osi odciętych, a wysokości są liczebnościami (częstościami) odpowiadającymi poszczególnym przedziałom klasowym. Taki sposób konstrukcji histogramu jest zasadny wówczas, gdy wszystkie przedziały klasowe są równe. W przeciwnym wypadku wysokości prostokątów są określone przez gęstości liczebności (częstości). Gęstość liczebności jest obliczana z następującego wzoru:

g_i - gęstość liczebności i-tej klasy,

n_i - liczebność i - tej klasy,

i - długość rozpiętość przedziału klasowego tzn różnica między górną i dolną granicą danej klasy.

Histogram skumulowany - na osi rzędnych odkłada się liczebności częstości skumulowane.

Diagram (wielobok liczebności) jest łamana powstałą przez połączenie punktów o współrzędnych: środki przedziałów klasowych i odpowiadające im liczebności (częstości lub gęstości). Diagram liczebności (częstości) skumulowanej jest natomiast łamaną powstałą przez połączenie punktów, których współrzędnymi są górne granice przedziałów klasowych i odpowiadające im (częstości) skumulowane. Diagram taki jest wykresem dystrybuanty empirycznej.

Czwartym etapem badania statystycznego jest opis lub wnioskowanie statystyczne. Opis statystyczny ma sumaryczny charakter i dotyczy tylko i wyłącznie danej zbiorowości statystycznej. Wnioskowanie statystyczne ma natomiast miejsce wówczas, kiedy badanie jest reprezentacyjne (próba losowa), a jego wyniki uogólniane są na całą populacje generalną, z której pochodzi próba.

Przedmiotem opisu statystycznego są zatem obserwacje badania pełnego, a jego narzędziem są odpowiednie miary zwane charakterystykami opisowymi (np. średnia arytmetyczna, odchylenie standardowe, współczynnik korelacji). Metody analizy badań pełnych (a wiec metody opisu statystycznego) wchodzą w zakres statystyki opisowej. W szczególności metodami tymi są metody opisu struktury, współzależności i dynamiki zjawisk masowych.

Podstawą wnioskowania statystycznego są empiryczne wyniki badania reprezentacyjnego (wyniki obserwacji losowo dobranej próby). Charakterystyki empiryczne obliczane z próby losowej nazywamy statystykami (np. średnia arytmetyczna z próby, odchylenie standardowe z próby, współczynnik korelacji z próby. Te same charakterystyki obliczane z obserwacji populacji generalnej noszą nazwę parametrów. Wartości statystyk zależą od wyników próby losowej. Jeśli próba jest reprezentatywna, to statystyki są dobrymi estymatorami parametrów populacji generalnej. Wraz ze wzrostem liczebności próby wartość estymatorów zbliża się do prawdziwych wartości parametrów.

4. STATYSTYKA OPISOWA

Podstawowa analiza danych powinna doprowadzić do zwięzłego przedstawienia ogólnej charakterystyki istotnych właściwości badanej zbiorowości. Liczby dające taki sumaryczny opis zbiorowości nazywamy parametrami statystycznymi. Parametry tak charakteryzują zbiorowość że porównywanie różnych zbiorowości statystycznych można sprowadzić do ich porównań.

Podstawowe zadania tych parametrów opisowych to:

• określenie przeciętnego rozmiaru i rozmieszczenia wartości zmiennej, dokonujemy tego przez obliczenie miar położenia,

• określenie granic obszaru zmienności wartości zmiennej, dokonujemy tego przez obliczenie miar zmienności,

• określenie skupienia i spłaszczenia (w stosunku do kształtu krzywej rozkładu normalnego) oraz stopnia zmiany od idealnej symetrii, dokonujemy tego przez obliczenie miar symetrii i koncentracji.

Najważniejsze i popularne są parametry wspomniane w dwóch pierwszych punktach.

5. MIARY POŁOŻENIA

Miary położenia dzielą się na przeciętne i kwantyle. Ich nazwa wywodzi się stąd że wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości zmiennej. Miary przeciętne charakteryzują średni lub typowy poziom wartości zmiennej (cechy) czyli mówią o przeciętnym poziomie rozważanej cechy

Średnie.

Średnią arytmetyczną definiujemy następującym wzorem:

gdzie x₁, x_{2, ...} , x_n ciąg wartości zmiennej

Przykład

W pewnym doświadczeniu medycznym bada się czas snu pacjentów leczonych na pewną chorobe. Zmierzono u n=12 losowo wybranych pacjentów czas snu i otrzymano następujące wyniki w minutach: 435, 389, 533, 324, 561, 395, 416, 500, 499, 397, 356, 398. Średni czas snu obliczamy korzystając z powyższego wzoru

Średnia arytmetyczna jest najlepszą miarą charakteryzującą rozkład cechy i dlatego jest miarą najczęściej używana. Obliczanie jej opiera się na wszystkich obserwacjach i ma ogromne znaczenie teoretyczne i praktyczne. Jedyną poważniejszą jej wadą jest to, że duży wpływ na nią wywierają najmniejsza i największa wartość badanego szeregu, czyli tzw. Skrajne wartości cechy (niejednokrotnie przypadkowo włączonych do próby). Często w praktyce (gdy pewnym pomiarom trzeba nadać większe znaczenie) oblicza się średnią arytmetyczną ważoną według wzoru:

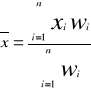
gdzie w_i tzw. wagi

Przykład

Przeprowadzono wśród pacjentów dwa testy psychomotoryczne. Oba oceniane w skali od 0 - 100. psycholog uznał, że waga wyników testów powinna być 2:3. Jeżeli osoba otrzymała z pierwszego testu 40 pkt, z drugiego 55 pkt to średnia ilość punktów liczona jest za pomocą średniej arytmetycznej. Otrzymujemy wiec:

oprócz średniej arytmetycznej można również wyróżnić inne rodzaje klasycznych miar tendencji centralnej w tym między innymi średnią geometryczną i średnią harmoniczną. Określa się je wzorami:

średnia geometryczna z liczb x₁, x₂, ... , x_n

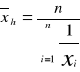
średnia harmoniczna z liczb x₁, x₂, ... , x_n

Obie średnie są mniejsze lub równe średniej arytmetycznej, przy czym równość zachodzi tylko dla identycznych wszystkich wartości. Średnią geometryczną stosujemy, gdy zjawiska są ujmowane dynamicznie (np. średnie tempo zmian). Średnie te są rzadziej wykorzystywane w problemach statystycznych w biologii i medycynie.

Modalna

Modalna (wartość najczęstsza) jest to wartość cechy statystycznej, która w rozkładzie empirycznym występuje najczęściej. Oznaczana jest symbolem M_o. W szeregach szczegółowych i rozdzielczych jest to wartość cechy, której odpowiada największa liczebność. Można więc łatwo określić przedział, w którym modalna występuje. Ogólny wzór na modalną ma następującą postać:

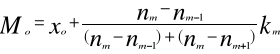
x_o - dolna granica przedziału w którym występuje modalna

n_m - liczebność przedziału modalnej

n_m-1 - liczebność klasy poprzedzającej przedział modalnej

n_m+1 - liczebność klasy następującej po przedziale modalnej

k_m - rozpiętość przedziału klasowego modalnej.

Przykład

W tabeli poniższej zestawiono liczbę pacjentów pewnej kliniki pogrupowanych według czasu działania leku przeciwbólowego.

Czas działania leku	8-12	13-17	18-22	23-27	28-32	33-37	38-42
Liczba pacjentów	4	29	39	81	25	9	4

Obliczamy modalną. Jak widać z tabeli, modalna występuje w czwartym przedziale.

Obliczając otrzymujemy :

KWANTYLE

Kwantyle to wartości cechy badanej zbiorowości (przedstawionej w postaci szeregu statystycznego), które dzieją zbiorowość na określone części pod względem liczby jednostek. Części te pozostają do siebie w określonych proporcjach. Do najczęściej stosowanych kwartyli należą kwartyle (podział na 4 części) i decyle (podział na 10 części) oraz percentyle (podział na 100 części).

• kwartyl pierwszy Q₁ jest to wartość jednostki, która dzieli zbiorowość w ten sposób, że ¼ (25%) jednostek ma od niej wartości większe, a ¾ (75%) nie mniejsze. Wyznaczenie Q₁ poprzedza ustalenie jego pozycji. Jest to przedział dla którego liczebność skumulowana jest mniejsza lub równa liczbie n/4 (n - liczebność zbiorowości).

• Kwartyl drugi (mediana wartość środkowa, Me) to wartość jednostki położonej w ten sposób że dzieli zbiorowość na dwie równe części. Mediana została wprowadzona do praktyki przez Pearsona w 1895 roku. Wyznaczenie mediany musi poprzedzić ustalenie jej pozycji. Jest to przedział dla którego liczebność skumulowana jest mniejsza lub równa liczbie n/2 (n - liczebność zbiorowości). Wówczas medianę obliczamy według wzoru:

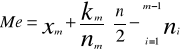
m - numer klasy w której występuje mediana

x_m - dolna granica tej klasy,

n_m - liczebność tej klasy

k_m - rozpiętośc tej klasy

- liczebność skumulowana do przedziału poprzedzającego klasę, w której występuje mediana.

Mediana obok średniej arytmetycznej jest najczęściej stosowanym parametrem statystycznym. Wartość mediany nie tylko zależy od wartości krańcowych. Możemy ją wyznaczyć nawet wtedy, gdy nie wszystkie obserwacje są dokładnie znane, np. z szeregów, w których występują nie zamknięte przedziały klasowe. Median wysuwa się na czoło w zastosowaniu do wszystkich wzrokowo uchwytnych, a trudno mierzalnych wielkości. Mediany używamy również do analizy cech jakościowych.

Przykład

W tabeli poniższej zestawiono liczbę pacjentów pewnej kliniki pogrupowanych według czasu działania leku przeciwbólowego.

Czas działania leku	8-12	13-17	18-22	23-27	28-32	33-37	38-42
Liczba pacjentów	4	29	39	81	25	9	4

Me=23+5/81*{201/2-72}=24,759

Oznacza to że dla połowy pacjentów czas działania leku nie przekracza 24,75 minut i dla takiej samej liczby pacjentów nie mniejszy od tej wartości.

Z szeregów wyliczających składających się z reguły z niewielkiej liczby jednostek medianę oblicza się wykorzystując do tego wzór:

Me

• kwartyl trzeci Q₃ jest to wartość jednostki, która dzieli zbiorowość w ten sposób, że ¾ (75%) jednostek ma od niej wartości niższe a ¼ (25%) wartości większe. Wyznaczenie Q₃ poprzedza ustalenie jego pozycji. Jest to przedział, dla którego liczebność skumulowana jest mniejsza lub równa od liczby 3n/4 (n liczebność zbiorowości).

Z kwartylami związana jest też charakterystyka zwana rozstęp kwartylny. Jest to różnica pomiędzy kwartylami trzecim i pierwszym. Rozstęp kwartylny (odchylenie ćwiartkowe) określa długość tej części przedziału zmienności cechy, w której znajduje się 50% środkowych obserwacji.

SZEREGI STATYSTYCZNE

Szczegółowe (wyliczające)

Rozdzielcze (strukturalne)

Przestrzenne (geograficzne)

Czasowe dynamiczne

momentów

okresów

Cech mierzalnych

Cech niemierzalnych

punktowe

przedziałowe

MIARY POŁOŻENIA

Średnia arytmetyczna

Średnia harmoniczna

Średnia geometryczna

Modalna

Kwantyle

Kwartyl pierwszy

Mediana (kwartyl drugi)

Kwartyl trzeci

Decyle

Gdy n jest nieparzyste

Gdy n jest parzyste

---