SPIS TREŚCI.

1. CAŁKA NIEOZNACZONA:

1. Całka nieoznaczona.

2. Funkcja pierwotna.

3. Całki funkcji elementarnych.

4. Tablica całek.

5. Podstawowe prawa całkowania.

6. Całkowanie funkcji trygonometrycznych.

7. Całkowanie funkcji wymiernej.

8. Całkowanie funkcji przestępnych (nie algebraicznych).

2. CAŁKA OZNACZONA:

1. Związek między całką oznaczoną a nieoznaczoną.

2. Definicja całki oznaczonej.

3. Własności całek oznaczonych.

4. Zastosowanie całek oznaczonych.

5. Zamiana zmiennej w całce oznaczonej.

6. Wyznaczenie objętości bryły na podstawie znajomości pół przekrojów równoległych.

7. Objętości bryły obrotowej.

8. Długość łuku krzywej płaskiej.

9. Pole powierzchni obrotowej.

10. Współrzędne środka ciężkości.

11. Całkowanie przybliżone.

12. Całki niewłaściwe:

• Całka niewłaściwa pierwszego rodzaju.

• Całka niewłaściwa drugiego rodzaju.

3. CAŁKI WIELOKROTNE, KRZYWOLINIOWE I POWIERZCHNIOWE:

1. Całka podwójna i jej obliczanie przez dwukrotne całkowanie.

2. Całka podwójna we współrzędnych biegunowych.

3. Obliczanie pól za pomocą całki podwójnej.

4. Masa, środek ciężkości i moment bezwładności.

5. Całka potrójna i jej obliczanie przez potrójne całkowanie.

6. Obliczanie wielkości za pomocą całki potrójnej.

7. Całki krzywoliniowe i ich obliczanie. Warunek niezależności od drogi całkowania.

8. Obliczanie wielkości za pomocą całek krzywoliniowych.

9. Całki powierzchniowe i ich obliczanie przez zamianę całki na podwójną.

10. Obliczanie wielkości za pomocą całek powierzchniowych.

CAŁKA NIEOZNACZONA.

Całka nieoznaczona funkcji
nazywamy rodzinę wszystkich pierwotnych i oznaczamy:

, gdy

• 
  - symbol całkowania

• 
  - funkcja podcałkowa

• 
  - stała całkowania

• 
  - zmienna całkowania

• 
  - wyrażenie podcałkowe

Funkcją pierwotną funkcji
określonej w przedziale
skończonym lub nie nazywamy każdą funkcję różniczkowalną
taką, że
dla każdego
. Jeżeli
jest funkcją pierwotną funkcji
, to każda inna funkcja pierwotna funkcji
jest równa
, gdzie
jest pewna stałą. Nie każda funkcja ma funkcję pierwotną. Te, które ją mają nazywamy funkcjami całkowalnymi.

Całki funkcji elementarnych:

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  
  
  

• 
  
  
  
  
  

Tablica całek:

1. 
   
   

2. 
   

3. 
   
   
   

4. 
   
   

5. 
   

6. 
   
   

7. 
   

8. 
   
   

9. 
   

10. 
    

11. 
    
    
    

12. 
    
    
    

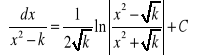
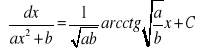
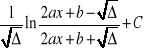
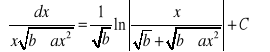
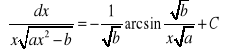
Podstawowe prawa całkowania:

• całkowanie przez podstawienie

, gdzie
i

• całkowanie przez części.

• całka z sumy (różnicy) funkcji

• całka z iloczynu funkcji przez stałą

, gdzie

Całkowanie funkcji trygonometrycznych.

Całki wyrażeń zawierających funkcje trygonometryczne o postaci:

1. 
   

2. 
   

3. 
   

4. 
   

można sprowadzić do podstawowych wzorów całkowania, a tym samym obliczać na podstawie następujących reguł:

1. Całki typu
   
   gdzie
   

1. Jeżeli n liczbą nieparzystą, to stosujemy podstawienie cos x = t przy obliczaniu pierwszej całki i sin x = t gdy obliczamy drugą całkę.

2. Gdy n jest liczbą parzystą to mamy do wyboru dwie możliwości:

1. przekształcić funkcję podcałkową wg wzorów (obniżenie wykładnika potęgi)

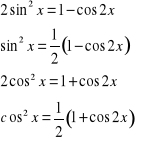
2. wykorzystując wzory rekurencyjne :

1. m - liczba nieparzysta
   
   

2. n - liczba nieparzysta
   
   

3. m, n - parzyste liczby
   ( wzory rekurencyjne)

2. Całki typu
   
   
   

1. Jeśli m jest liczbą nieparzystą, to podstawiamy cos x = t

2. Jeśli n jest liczbą nieparzystą, to podstawiamy sin x = t

3. Jeśli obie liczby są parzyste, to przekształcamy funkcję podcałkową wykorzystując do tego wzory

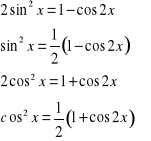
3. Całki typu
   ,
   

Obliczamy przez podstawienie nowej zmiennej, zamiast
lub odpowiednio
.

4. Całki typu
   ,
   ,
   

Obliczamy przez przekształcenie iloczynów wyrażeń podcałkowych na sumę, wg wzorów:

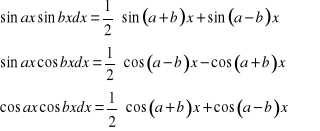
Całkowanie funkcji wymiernej.

Funkcją wymierną nazywamy funkcję postaci
,
, gdzie
(wielomian stopnia k-tego)

• 
  - funkcja wymierna niewłaściwa

• 
  - funkcja wymierna właściwa

Uwaga:

Każdy wielomian
może być przedstawiony w postaci iloczynu dwumianów
lub trójmianów

- rozkład na ułamki proste w postaci

,

1. Jeżeli
   

to:

2. 
   
   - rozkład na ułamki proste

3. 
   to
   

4. 
   
   doprowadzenie do pochodnej mianownika i zastosowanie

wzoru na arctg .

tzn

Całkowanie funkcji przestępnych (nie algebraicznych).

Do całek funkcji wymiernych sprowadzają się następujące całki (R - funkcja wymierna):

1. 
   

przez podstawienie

;

wtedy

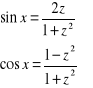
oraz

2. 
   

przez podstawienie

;

wtedy

3. 
   

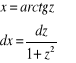
przez podstawienie

;

wtedy

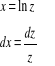
CAŁA OZNACZONA.

Związek między całką oznaczoną a nieoznaczoną.

Jeżeli przez F(x) oznaczymy funkcję pierwotną funkcji f(x), ciągłej w przedziale
, tzn. jeżeli F'(x) = f(x), to ma miejsce wzór

,

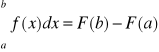
przy czym różnica F(b) - F(a) nie zależy od stałej całkowania C.

Prawą stronę równania oznacza się symbolem

lub
.

Jeżeli u, v są funkcjami zmiennej x mającymi ciągłą pochodną, to

.

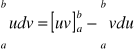
Jest to wzór na całkowanie przez części dla całek oznaczonych.

Jeżeli g'(x) jest funkcją ciągłą, g(x) funkcją rosnącą w przedziale
, a f(u) funkcją ciągłą w przedziale
to zachodzi następujący wzór:

.

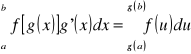
Jest to wzór na całkowanie przez podstawienie dla całek oznaczonych.

Definicja całki oznaczonej.

Jeżeli:

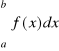
= F(x) + c,

to

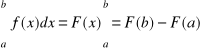
W interpretacji geometrycznej całka oznacza pole obszaru płaskiego zawartego między linią linią y=f(x)
0 i osią X

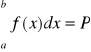
W ogólności:

P=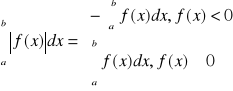

Dla f(x)≥0

P=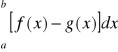

Gdy g(x)=0, to z poprzedniego wzoru otrzymujemy:

P=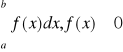

Właściwości całek oznaczonych.

Z definicji całki mamy:

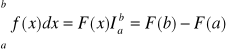
Warunki:

• f(x)≥0 =>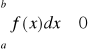
  

• f(x)<0 =>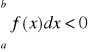
  

• f(x)≤g(x) =>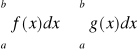
  

• 
  

• 
  

• 
  

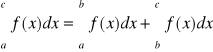
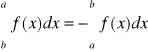
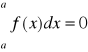
Z interpretacji geometrycznej całki można zauważyć, iż wzór 4⁰ jest prawdziwy przy dowolnym układzie liczb a,b,c.

Całka sumy równa się sumie całek, co można zapisać:

.

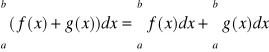
Powyższy wzór jest to tzw. addytywność całki względem funkcji podcałkowej.

Całka oznaczona posiada własność liniowości. Wzór ten należy rozumieć w ten sposób, że z istnienia całek po prawej stronie wynika istnienie całki po lewej stronie oraz podana równość.

Również prawdziwy jest wzór:

,

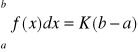
gdzie K jest liczbą spełniającą nierówność m ≤ K ≤ M, przy czym m oznacza kres dolny, a M kres górny funkcji f(x) w przedziale <a,b>.

Na podstawie własności Darboux, która mówi, że funkcja ciągła przybiera wszystkie wartości pośrednie pomiędzy swoimi kresami górnym i dolnym, wzór powyższy można zapisać w postaci:

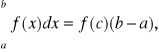
gdzie c jest liczbą spełniającą nierówność a ≤ c ≤ b, jeżeli funkcja podcałkowa f(x) , jest ciągła w przedziale <a,b>.

Całka jako funkcja górnej granicy.

Jeżeli funkcja f(t) jest ciągła w przedziale <a,b>, to funkcja

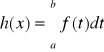
jest ciągła i różniczkowalna wzglądem zmiennej x w przedziale <a,b> i w każdym punkcie tego przedziału zachodzi związek h'(x)=f(x).

Zastosowanie całek oznaczonych.

1. Krzywa określona jest funkcją y=f(x), xє[a,b]

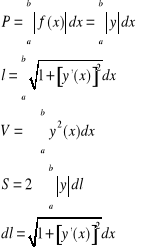
bryła powstała z obrotu krzywej y=f(x) dookoła osi OX.

2. Krzywa określona jest w postaci krzywej parametrycznej [x=x(t), y=y(t)].

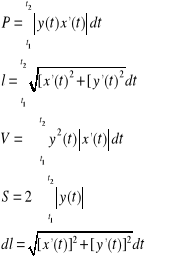
3. Krzywa określona jest w układzie biegunowym ζ=ζ(φ)

Ponieważ każda krzywa w układzie biegunowym sprowadza się do układu kartezjańskiego za pomocą związków to jest ona określona za pomocą:

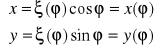
Pole, długość, objętość, pole powierzchni obliczamy tak samo jak krzywą określoną w postaci parametrycznej.

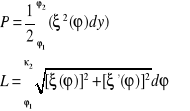
Zamiana zmiennej w całce oznaczonej.

Przy obliczeniu niektórych całek oznaczonych pożyteczne jest wprowadzenie nowej zmiennej całkowanie. Przy tym, jeżeli całka oznaczona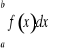
przekształcana jest za pomocą podstawienia
(lub
) na inną całkę z nową zmienną całkowania
, to poprzednie granice
i
należy zastąpić przez nowe granice całkowania
i
, które wyznaczamy na podstawie przyjętego podstawienia, czyli z równań
,
(albo
,
).

Jeśli
oraz
są ciągle w przedziale
, to zachodzi:

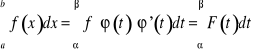
Wyznaczanie objętości bryły na podstawie znajomości pól przekrojów równoległych.

Gdy znane jest pole S(x) dowolnego przekroju danej bryły płaszczyzną równoległą do płaszczyzny P , gdzie x oznacza odległość płaszczyzny tnącej od płaszczyzny P, to przy zmianie x o wielkość dx różniczką objętości będzie objętość walca prostego o wysokości dx i o polu podstawy S(x), czyli dV= S(x)dx, a objętość bryły wyrazi się całką:

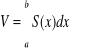
przy czym a i b stanowią odpowiednio lewą i prawą granicę przedziału zmienności
.

Objętość bryły obrotowej.

Jeśli pewna bryła powstaje przez obrót trapezu krzywoliniowego
dookoła osi
, to każdy z jej płaskich przekrojów, prostopadłych do osi
, stanowić będzie koło o promieniu równym odpowiedniej rzędnej krzywej
.

Pole przekroju
odpowiadającego odciętej
, jako pole koła, będzie równe
.

Różniczką objętości odpowiadającą przyrostowi
będzie
, a całkowitą objętość bryły obrotowej określa wzór:

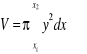
Gdy natomiast bryła powstaje przez obrót trapezu krzywoliniowego
wokół osi
,

to
oraz

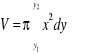
Długość łuku krzywej płaskiej.

Jeśli krzywa płaska, rozpatrywana w układzie współrzędnych prostokątnych, jest dana równaniem
lub
, albo w postaci parametrycznej

,

to różniczka
długości jej łuku wyraża się wzorem:

a długość łuku określona jest wzorem:

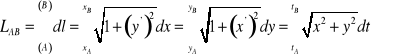
Pole powierzchni obrotowej.

Jeśli powierzchnia powstaje na skutek obrotu łuku
krzywej płaskiej wokół osi
, to różniczka pola tej powierzchni bocznej kołowego stożka ściętego, o tworzącej
i promieniach podstawy
i

a pole powierzchni, utworzonej przez obrót łuku AB, jest określone wzorem

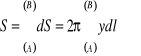
przy czym
określają wartość obranej zamiennej całkowania w punktach A i B,

a
- różniczkę łuku krzywej.

Jeśli obrót łuku odbywa się wokół osi
to,

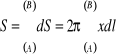
Współrzędne środka ciężkości.

Środkiem ciężkości zbioru punktów materialnych nazywamy punkt przyłożenia wypadkowej równoległych sił ciężkości, przyłożonych w tych punktach.

Dla łuku materialnego AB krzywej płaskiej współrzędne prostokątne środka ciężkości C są określone wzorami:

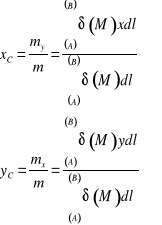
gdzie: m - masa luku ,
i
- momenty styczne łuku względem osi Ox i Oy,
- gęstość liniowa rozkładu masy w punkcie
łuku,
- różniczka długości łuku, a
i
- wartość obrabianej zmiennej całkowania w punktach końcowych A i B.

W przypadku gdy łuk materialny jest jednorodny, wzory upraszczają się, gdyż stałą
można wtedy wynieść przed znaki całek.

Współrzędne środka ciężkości jednorodnego trapezu krzywoliniowego, przylegającego do osi Ox , dane są wzorami:

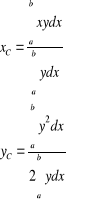
Jeśli jednorodna linia materialna lub figura mają oś symetrii, to środek ciężkości tej linii (figury) leży na tej osi.

Całkowanie przybliżone.

Istnieje kilka sposobów przybliżonego całkowania. Jeśli funkcja
dana jest albo za pomocą pewnego wzoru, albo za pomocą tablic jej wartości, to całkę oznaczoną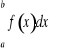
możemy obliczyć w sposób następujący:

1. dzielimy przedział całkowania
   na
   równych części
   za pomocą punktów
   ,

2. obliczamy wartości funkcji podcałkowej
   w punktach podziału, czyli obliczamy:

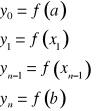
3. posługujemy się którymkolwiek ze wzorów całkowania przybliżonego.

Najczęściej stosowane są następujące przybliżone wzory, oparte na geometrycznym przedstawieniu całki oznaczonej jako pola trapezu krzywoliniowego.

1. Wzór prostokątów

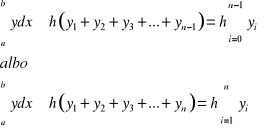
Geometrycznie wzór ten oznacza zastąpienie pola trapezu krzywoliniowego, odpowiadającego całce
, sumą pól prostokątów. Błąd powstały przy przybliżonym obliczaniu całki oznaczonej wg wzorów prostokątów ma oszacowanie:

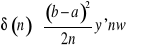
gdzie
- największa z wartości
w przedziale
.

2. Wzór trapezów.

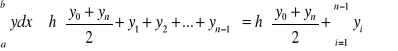
Geometrycznie wzór ten oznacza zastąpienie pola trapezu krzywoliniowego sumą pól trapezów. Błąd we wzorze trapezów ma oszacowanie:

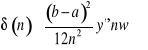
gdzie
- największa z wartości
w przedziale
.

3. Wzór trapezów parabolicznych (czyli wzór Simpsona);n jest tu liczbą parzystą.

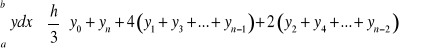
Geometrycznie na podstawie tego wzoru pole każdej pary pasków jest zastępowane polem trapezu parabolicznego, powstaje dzięki zastąpieniu łuku krzywej
łukiem paraboli
(o osi pionowej), przechodzącej przez trzy punkty krzywej o odciętych:

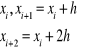
Błąd wzoru Simpsona ma oszacowanie

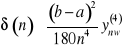
gdzie
- największa z wartości
w przedziale
.

Oczywiście, każdy z podanych tu wzorów będzie dokładniejszy, im więcej będzie punktów podziału, czyli im większe będzie
. Inaczej mówiąc, przy dostatecznie dużej wartości
za pomocą każdego z tych wzorów można obliczyć wartość przybliżoną całki oznaczonej z dowolną dokładnością.

Przy jednakowej liczbie podziałów
, drugi wzór jest na ogół dokładniejszy od pierwszego, pierwszego, pierwszego trzeci bardziej dokładny niż drugi.

Całki niewłaściwe.

Całkami niewłaściwymi nazywamy całki oznaczone, w których albo granice całkowania są nieskończone, albo funkcja podcałkowa jest nieciągła.

1. Całka niewłaściwa pierwszego rodzaju.

1. Funkcja podcałkowa f(x) nie jest ograniczona w otoczeniu punktu x = b, wówczas całkę określamy następująco:

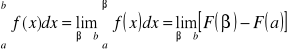
, a < β < b,

jeśli ta granica istnieje.

2. Funkcja podcałkowa f(x) nie jest ograniczona w otoczeniu punktu x = a, wówczas całkę określamy następująco:

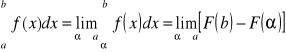
, a < α < b,

jeśli ta granica istnieje.

3. Jeżeli natomiast funkcja podcałkowa f(x) nie jest ograniczona w pewnym otoczeniu punktu x = c, gdzie a < c < b, to całkę określamy następująco:

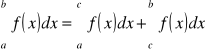
2. Całka niewłaściwa drugiego rodzaju.

1. Funkcja f(x) jest określona i ciągła w przedziale
   , wówczas całkę funkcji f(x) w przedziale
   określamy następująco:

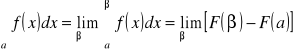
Jeżeli granica po prawej stronie nie istnieje, to mówimy, że całka niewłaściwa nie istnieje.

2. Jeżeli niewłaściwość występuje na lewym końcu przedziału całkowania
   , to całkę określamy następująco:

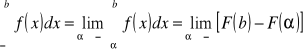
3. Przyjmijmy także określenie:

,

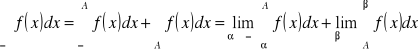
gdzie A jest dowolną liczbą.

Jeżeli istnieją skończone granice określające całki niewłaściwe pierwszego i drugiego rodzaju, to całki te nazywamy zbieżnymi. W przeciwnym razie nazywamy je rozbieżnymi.

18

---