Numer ćwiczenia
7 |
Temat ćwiczenia
Samoindukcja cewki
|
Ocena z teorii |
Numer zespołu
|
Nazwisko i imię
Fiołek Robert
|
Ocena zaliczenia ćwiczenia
|
Data
01.03.2006 |
Wydział, rok, grupa
EAIiE, AiR rok I, gr. I
|
Uwagi |
Cel ćwiczenia
Wyznaczenie współczynnika samoindukcji cewki poprzez porównanie impedancji dla prądu zmiennego i rezystancji dla prądu stałego.
Wprowadzenie
W cewce, przez którą przepływa prąd, pojawia się indukowana siła elektromotoryczna SEM. Podlega ona prawu indukcji Faradaya, jak każda indukowana SEM. Kierunek SEM samoindukcji wyznaczamy z reguły Lenza, która mówi, że kierunek prądu indukowanego, przeciwstawia się zmianie, która go wywołała. Wartość natężenia prądu nie wpływa na wartość SEM, istotna jest natomiast szybkość zmian natężenia prądu. Zakładamy, że przez cewkę płynie prąd I wytwarzany przez baterię. Po odłączeniu baterii z obwodu SEM natychmiastowo spada do zera, co spowoduje zmniejszanie się prądu I. Zmiana ta, w terminologii Lenza, jest zmianą, której musi przeciwdziałać samoindukcja. Aby zapobiec zmniejszaniu się I, indukowana SEM musi mieć ten sam kierunek, co prąd. Kiedy prąd w cewce wzrasta, z reguły Lenza wynika, że SEM samoindukcji ma kierunek przeciwny do kierunku prądu. W każdym z tych dwóch przypadków SEM samoindukcji działa tak, aby zapobiec zmianie prądu. Tłumaczy to również znak minus w równaniu opisującym SEM.
Wymagane wiadomości teoretyczne
prawo Ohma - mówi o tym, że wraz ze wzrostem napięcia na danym odbiorniku rośnie wprost proporcjonalnie natężenie prądu płynącego przez ten odbiornik, a współczynnikiem proporcjonalności jest jego rezystancja, która jest stała. Prawo to opisuje równanie:
U=IR
prawo indukcji Faradaya - indukowana w obwodzie siła elektromotoryczna (SEM) równa jest wziętej ze znakiem ujemnym szybkości zmian strumienia ΦB indukcji magnetycznej przechodzącego przez ten obwód. Wielkość SEM opisuje równanie:
ε = -dΦB/dt (∫Edl = -dΦB/dt)
samoindukcja cewki - jest to zjawisko pojawiania się indukowanej SEM (siły elektromotorycznej samoindukcji) w pojedynczej cewce pod wpływam zmian natężenia prądu płynącego przez tą cewkę. Jak każda indukowana SEM podlega prawu indukcji Faradaya, które dla np. dla ściśle nawiniętej cewki przyjmuje postać
ε = -d(NΦB)/dt
(N - liczba zwojów, NΦB - wypadkowy strumień przechodzący przez wszystkie zwoje). Iloczyn NΦB jest ważną wielkością charakterystyczną dla indukcji. Dla danej cewki, oddalonej od wszelkich materiałów magnetycznych wielkość ta jest proporcjonalna do natężenia prądu i płynącego w cewce
NΦB = Li
gdzie L jest stałą proporcjonalności, nazywaną indukcyjnością cewki. Można więc zapisać
ε = -d(NΦB)/dt = -Ldi/dt
z czego otrzymujemy wzór na indukcyjność:
L = -ε/(di/dt) [L]=1henr [H]=1Vs/A.
(ε i di/dt mają przeciwne znaki, bo L zawsze jest dodatnie).
rezystancja - (opór elektryczny czynny) jest wielkością charakterystyczną dla danego elementu elektrycznego. Jest to stosunek różnicy potencjałów na końcach tego elementu do natężenia prądu przepływającego przez niego. Jest to, zatem miara oporu, jaki dany element stawia przepływowi ładunku elektrycznego.
R = U/I [R] = 1Ω (om)
Rezystancja przewodu jest wprost proporcjonalna do jego długości, a odwrotnie proporcjonalna do jego przekroju:
R=ςl/S
reaktancja - (opór bierny) jest właściwością obwodu elektrycznego zawierającego pojemność elektryczną, która wraz z oporem czynnym tworzy opór elektryczny pozorny.
Dla cewki: XL=ωL
Dla kondensatora: XC=1/ωC
W szczególnym przypadku szeregowo połączonych elementów o indukcyjności L i pojemności C wypadkowa reaktancja wynosi
X = ωL-1/(ωC) ω=2Лf
impedancja - czyli opór pozorny Z jest dany wzorem
Z2 = R2 + X2
gdzie R jest oporem czynnym danego obwodu, a X oporem biernym.
konduktancja - przewodność elektryczna czynna przewodnika w obwodzie prądu stałego co do wartości równa odwrotności wartości rezystancji
G = 1/R [G] = 1S (simens)
admitancja - (przewodność elektryczna pozorna) pojęcie wprowadzane przy przepływie przez przewodnik prądu sinusoidalnie zmiennego, jest wielkością zespoloną, której moduł jest równy
|Y| = √(G2 + B2)
susceptancja - to przewodność elektryczna bierna B, część urojona admitancji
przesuniecie fazowe - występuje miedzy zmiennym napięciem i prądem w obwodzie elektrycznym zawierającym oprócz oporu czynnego także opór bierny. Przykładowo, jeżeli do kondensatora przyłożymy napięcie sinusoidalnie zmienne: U(t) = U0cos(ωt), to zgodnie z równaniem Q = CU ładunek kondensatora będzie opisany równaniem:
Q(t) = CU0cos(ωt)
Zmiana ładunku kondensatora oznacza, że płynie prąd przemienny. Ponieważ I = dQ/dt, więc podstawiając wcześniejszą zależność i obliczając pochodną otrzymujemy:
I(t) = -ω C U0 sin(ωt)
Wynika z tego, że na kondensatorze prąd wyprzedza napięcie o kąt π/2, co jest częstotliwość resztą logiczne, gdyż najpierw płynie przez niego prąd ładowania częstotliwość potem stopniowo rośnie napięcie.
częstotliwość - f [Hz] - liczba pełnych cykli drgań okresowych w jednostce czasu określona w hercach liczbowo równa odwrotności okresu drgań
częstość - ω - liczba określonych zdarzeń zachodzących w jednostce czasu
krzywa namagnesowania ferromagnetyka - wykres obrazujący zależność wartości namagnesowania rdzenia ferromagnetycznego BM od wartości B0. Pętla przyjmuje rozmiary charakterystyczne dla danej substancji, jednak ogólny jej kształt i punkty ją charakteryzujące występują w każdym rozpatrywanym przypadku.
|
0- rozmagnesowana substancja A, D- stan nasycenia B, E- zmiana kierunku prądu C, F- pełne rozmagnesowanie 0A- krzywa namagnesowania pierwotnego 0B, 0E- pozostałość magnetyczna 0C, 0F- koercja
|
Cewka 1
Konduktancja: G = 69,73mS
Admitancja: Y = 2,79mS
Obliczam rezystancję zwojów:
R=![]()
R=![]()
= 14,34Ω
Obliczam impedancję i reaktancję cewki:
Z=![]()
Z=![]()
= 358,42Ω
Z = ![]()
![]()
![]()
358,13Ω
Obliczam indukcyjność:
L = ![]()
, ![]()
, f = 50[Hz] L=1,14H
Obliczam błąd pomiaru ∆L metodą różniczki zupełnej:
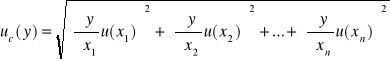
L = 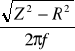
, czyli L(Z,R), bo 2πf jest stałe, zatem
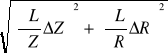
ΔL =
Obliczamy najpierw ∆Z oraz ∆R, aby potem zastosować prawo przenoszenia niepewności:
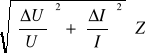
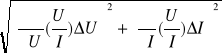
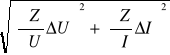
∆Z= = =
Dla prądu zmiennego ∆U=0,01V Uśr=6,5V ∆I=0,0001A Iśr=0,0225A zatem:
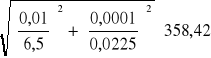
∆Z= = 1,7Ω
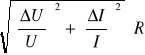
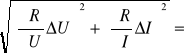
∆R=
Dla prądu stałego ∆U=0,01V Uśr=6,5V ∆I=0,001A Iśr=0,458A zatem:
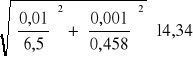
∆R= = 0,04Ω
Obliczam teraz błąd ΔL:
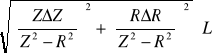
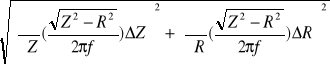
ΔL= =
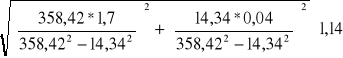
ΔL= = 0,006H
Obliczam kąt przesunięcia fazowego:
tg![]()
= ![]()
= ![]()
![]()
= arctg(![]()
)= arctg(![]()
)= 87,7o
Cewka 2
Obliczenia są analogiczne jak dla cewki 1:
Konduktancja: G=32,31mS
Admitancja: Y=1,4mS
R=31Ω
Z=714,3Ω
XL=713,6Ω
L=2,27H
Dla prądu zmiennego ∆U=0,01V Uśr=6,5V ∆I=0,00001A Iśr=0,01095A zatem:
∆Z=1,3Ω
Dla prądu stałego ∆U=0,01V Uśr=6,5V ∆I=0,001A Iśr=0,21A zatem:
∆R=0,16Ω
ΔL=0,004H
![]()
=87,5o
Wnioski:
Na wykresach wyraźnie widać, że nachylenie prostej I=f(U) jest mniejsze dla prądu zmiennego, czyli jest mniejsza konduktancja. Jest to spowodowane pojawieniem się zjawiska samoindukcji, które wywołuje reaktancję i zmniejsza wartość prądu płunącego w obwodzie. W przypadku, gdy przez cewki płynął prąd zmienny, punkty pomiarowe nie układały się liniowo, co było spowodowane nasycaniem się rdzenia wraz ze wzrostem prądu przepłuwającego przez cewki, a co za tym idzie, zwiększenie indukcyjności oraz reaktancji cewek.
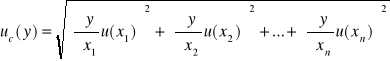
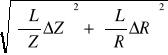
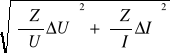
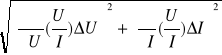
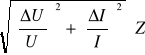
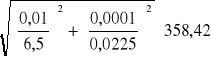
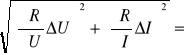
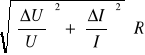
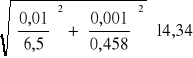
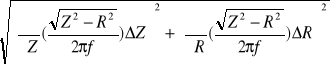
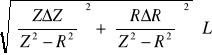
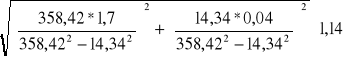
Wyszukiwarka
Podobne podstrony:
Indukcja wzajemna, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labork
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
WICZENIE8 12 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
wspolczynnik zlamania sprawozdanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Lab
Sprawozdanie lab3, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labork
poziomy energetyczne sprawozdanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Labo
35 Elektroliza2222, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
hall sprawozdanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labork
Sprawozdanie z praktyk wakacyjnych, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Lab
lab 71, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki
SPRAWOZDANIE Z MATLABA, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
5 OSKOT, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Labork
SP DZWI K MOJE , Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
sprawozdanie v2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
10 W EM, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki
WICZENIE12 4 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYKA3, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki
dozymetria promieniowania gamma, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Labora
więcej podobnych podstron