Funkcje wielu zmiennych.
Obliczyć wskazane pochodne cząstkowe podanej funkcji:
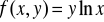
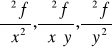
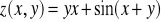
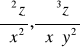
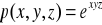
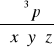
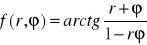
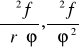
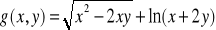
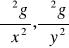
Wyznaczyć różniczkę zupełną funkcji:
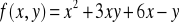
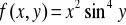
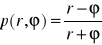
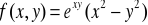
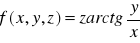
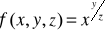
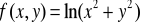
Sprawdzić, czy dana funkcja spełnia podane równanie:
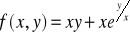
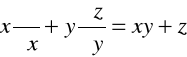
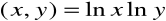
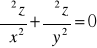
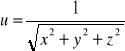
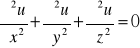
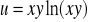
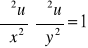
Wyznaczyć ekstrema funkcji:
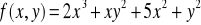
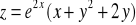
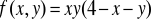
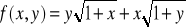
Obliczyć gradient funkcji:
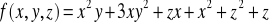
w P(-1,1,0)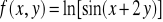
w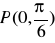
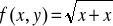
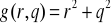
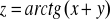
Znaleźć pochodną funkcji
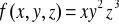
w A(3,2,1) w kierunku wektora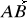
, gdzie B(5,4,2).Znaleźć pochodną funkcji
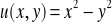
w M(1,0) w kierunku wektora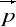
, tworzącego kąt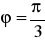
z dodatnim zwrotem osi )x.Obliczyć pochodną funkcji w kierunku gradientu tej funkcji w punkcie P, gdy
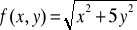
, P(2,1).Obliczyć pochodne kierunkowe funkcji określonych wzorami:
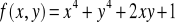
w P(1,2) w kierunku wektora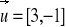
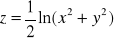
w A(1,1) w kierunku wersora dwusiecznej kąta pierwszej ćwiartki układu )xy.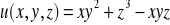
w B(1,1,2) w kierunku wektora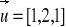
.Obliczyć przybliżoną wartość wyrażenia:
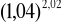
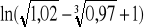
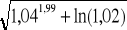
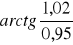
Wyznaczyć ekstrema funkcji uwikłanej określonej równaniem:
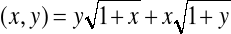
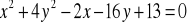
, f(1)=3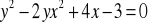
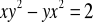
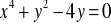
Wyszukiwarka
Podobne podstrony:
Matematyka III (Ćw) Lista 06 Ekstrema lokalne i globalne funkcji wielu zmiennych Zadania
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
analiza matematyczna funkcje wielu zmiennych pwn
Ćwiczenia z Matematyki, Zadania - Funkcje Wielu Zmiennych, Elementy logiki i teorii mnogości
Wykłady z Matematyki, Wykłady - Rachunek Różniczkowy Funkcji Wielu Zmiennych, Dr Adam Ćmiel
Funkcje wielu zmiennych, Studia Budownictwo UZ, 1 semestr, Matematyka, Wyklady matematyka
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Zadania
Matematyka III (Ćw)-Lista 06-Ekstrema lokalne i globalne funkcji wielu zmiennych, Odpowiedzi 2
Matematyka III (Ćw) - Lista 06 - Ekstrema lokalne i globalne funkcji wielu zmiennych, Zadania
Matematyka III (Ćw) Lista 06 Ekstrema lokalne i globalne funkcji wielu zmiennych Odpowiedzi 2
Matematyka III (Ćw) Lista 05 Rachunek rózniczkowy funkcji wielu zmiennych Odpowiedzi
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
funkcje wielu zmiennych UWM id Nieznany
10 Funkcje wielu zmiennych
11 RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
ek mat ii optymalizacja funkcji wielu zmiennych
140 Funkcje wielu zmiennych
więcej podobnych podstron