Sprawozdanie

Politechnika Śląska

Wydział A E i I

Kierunek A i R

Ćwiczenie laboratoryjne z fizyki:

Pomiar prędkości dźwięku w powietrzu. Metody: rezonansowa i przesunięcia fazowego.

Grupa sekcja

Gliwice

1.1 Fala akustyczna

Rozchodzenie się dźwięku w powietrzu jest zjawiskiem falowym. Jest to zaburzenie rozchodzące się w ośrodku sprężystym ( powietrzu ), polegające na przenoszeniu energii przez drgające cząstki ośrodka bez zmiany ich średniego położenia. Fala akustyczna jest sprężystą falą podłużną. Równanie tej fali rozchodzącej się wzdłuż osi x, w dwóch punktach odległych od siebie o r ma postać: y1 = A cos [ 2 ( t/T - x/ ) + δ ] y2 = A cos [ 2 ( t/T - (x + r)/ ) + δ ] . Między falą w punkcie 1 i 2 istnieje dodatkowa różnica fazy δ   r/c gdzie c - prędkość propagacji fali. Zakładając że w punktach 1 i 2 są dwa kolejne węzły otrzymujemy:  =  ri i /c -  ri-1/c . Podstawiając: δri = ri - ri-1 otrzymujemy: c = 2 δri. Analogicznie postępując możemy otrzymać wzór w którym zmieniana jest częstotliwość - dla tegosamego punktu po zmianie częstotliwości powinniśmy otrzymać ponownie węzeł. Wzór na prędkość propagacji fali ma wtedy postać: c = 2r δi

Rozchodzenie się fali jest równierz procesem termodynamicznym. Zagęszczenia i rozrzedzenia ośrodka, który jest nośnikiem fali, są adiabatyczne - ze względu na dużą szybkość propagacji fali w powietrzu. Znając cp/cv =  można wzór na propagację fali w powietrzu zapisać w postaci:

gdzie R- uniwersalna stała gazowa, T- temperatura w kelwinach, - masa molowa powietrza.

1.2. Fale stojące

W wyniku interferencji dwóch fal, biegnących na przeciw siebie, o równaniach: y1 = A cos  ( t/T - x/ ) y2 = A cos  ( t/T + x/ ) otrzymamy falę wypadkową o równaniu : y = y1 + y2 = 2A cos  x/ cos  t/T Analizując powyższe równanie otrzymujemy warunki na istnienie fali stojącej. W przypadku rury Kundta, gdy fala jest ograniczona dwoma ośrodkami gęstszymi warunek ten przyjmuje pstać: l = (2n +1 )/4, co oznacza, że fala stojąca wytworzy się tylko w rurze o takiej długości, gdy mieści się w niej nieparzysta liczba ćwiartek fal. Analizując równanie fali można również podać warunki na istnienie węzłów i strzałek. Węzły, czyli punkty w których nie występują drgania powstają w miejscach spełniającym warunek: x = (2n +1 )  /4 , a strzałki, czyli punkty w których amplituda drgań jest maksymalna, powstają w punktach spełniających warunek: x = n  /2.

2.1. Schematy układów

W pierwszej części ćwiczenia dokonywano pomiaru prędkości dźwięku w powietrzu metodą rezonansową. W celu dokonania pomiarów zbudowano układ według schematu przedstawionego poniżej.

Schemat 1. G- generator, F- częstotliwościomierz, 1-głośnik, 2-rura Kundta, 3-mikrofon, 4-oscyloskop

W części drugiej ćwiczenia dokonywano pomiarów metodą przesunięcia fazowego. Zbudowano układ według schematu zamieszczonego poniżej.

Schemat 2. Oznaczenia jak powyżej.

2.2 Krótki opis przebiegu ćwiczenia

W części pierwszej ćwiczenia zbudowano układ jak na schemacie 1. Zdejmowano pomiary za pomocą metody rezonansowej. Pomiarów dokonywano w następujący sposób: 1. Ustawiano częstotliwość f0 i szukano takiego położenia mikrofonu by wskaznie na oscyloskopie było maksymalne ( strzałka ). 2. Nie zmieniając położenia mikrofnu szukano dwóch najbliższych wartości częstotliwości odpowiadających rezonansowi akustycznemu. Ogółem dokonano 5 serii pomiarów według powyżej przedstawionej kolejności.

Wczęści drugiej mierzono prędkość dźwięku metodą przesunięcia fazowego. Zbudowano układ jak na schemacie 2. Pomiarów dokonywano według następującej kolejności: 1. Ustawiano częstotliwość. 2. Szukano takich położeń mikrofonu, kiedy na ekranie oscyloskopu elipsa przechodziła w prostą skośną. Notowano pięć kolejnych takich płożeń. Ogółem dokonano pomiarów dla 3 różnych częstotliwości.

3. Obliczenia i analiza błędów

Do obliczeń przyjęto następujące wartości błędów wynikających z niedokładności odczytu i niedoskonałości mierników: l = 0.005 [m] - błąd odczytu z przymiaru,  = 1 [Hz] - błąd częstotliwościomierza, T = 0.5 [° C] - błąd odczytu z termometru.

Metoda rezonansowa.

Wstawiając do wzorów : c = 2 l |  - | c = 2 l |  - | obliczono następujące prędkości dźwięku w powietrzu: c1=346.5 [m/s] c2=316.0 [m/s] c3=323.4 [m/s] c4=357.0 [m/s] c5=374.9 [m/s] c6=342.3 [m/s] c7=357.6 [m/s] c8=344.0 [m/s] c9=350.1 [m/s] c10=342.9 [m/s]

Następnie ze wzoru na różniczkę zupełną obliczono błąd, który wyraża się wzorem: c = | 2 | | l | + | 2 l | || Po wstawieniu odpowiednich danych uzyskano następujące błędy dla odpowiednich prędkości: Dc1=7.4 [m/s] Dc2=6.8 [m/s] Dc3=6.0 [m/s] Dc4=6.6 [m/s] Dc5=5.7 [m/s] Dc6=5.6 [m/s] Dc7=5.3 [m/s] Dc8=5.1 [m/s] Dc9=4.8 [m/s] Dc10=4.7 [m/s] Stosując wzór na średnią ważoną otrzymano wartość prędkości dźwięku w powietrzu: c=343.8 [m/s] , oraz błąd średniej ważonej: c=1.8 [m/s]

Metoda przesunięcia fazowego

Obliczono odległości między strzałkami dla danych czestotliwości: 2000 Hz x1=8.6 [cm] x2=8.7 [cm] x3=8.6 [cm] x4=8.5 [cm] 2500 Hz x1=6.9 [cm] x2=7.0 [cm] x3=7.0 [cm] x4=7.0 [cm] 3000 Hz x1=5.8 [cm] x2=5.6 [cm] x3=5.8 [cm] x4=5.7 [cm] . Następnie wstawiając do wzoru: c = 2 x  otrzymano następujące wartości c : c1=344.0 [m/s] c2=348.0 [m/s] c3=344.0 [m/s] c4=340.0 [m/s] c5=345.0 [m/s] c6=350.0 [m/s] c7=350.0 [m/s] c8=350.0 [m/s] c9=348.0 [m/s] c10=336.0 [m/s] c11=348.0 [m/s] c12=342.0 [m/s] Ze wzoru na różniczkę zupełną wyprowadzono wzór na błąd wyznaczenia c tą metodą: c = | 2n | | l | + | 2x | |  | Po podstawieniu odpowiednich danych otrzymano odpowiednio dla każdej prędkości następujące błędy: Dc1=20.2 [m/s] Dc2=20.2 [m/s] Dc3=20.2 [m/s] Dc4=20.2 [m/s] Dc5=25.1 [m/s] Dc6=25.1 [m/s] Dc7=25.1 [m/s] Dc8=25.1 [m/s] Dc9=30.1 [m/s] Dc10=30.1 [m/s] Dc11=30.1 [m/s] Dc12=30.1 [m/s] . Wstawiając do wzoru na średnią ważoną otrzymano następującą wartość c: c=345.4 [m/s] oraz błąd średniej ważonej : c=7.0 [m/s]

Następnie obliczono wykładniki adiabaty , stosując poniższy wzór:

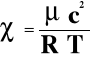
gdzie R=8.31 [J/ (mol K)], =28.87E-3 [kg/mol], T=293.5 [K]. Podstawiając uzyskane prędkości c z obu części ćwiczenia, oraz pozostałe dane otrzymano następujące wartości stałej   1.41 Błąd wyznaczenia c obliczano według wzoru: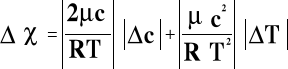

Po wstawieniu danych otrzymano:

1=0.02 =0.06 gdzie 1,- dla metody rezonansowej, ,- dla metody przesunięcia fazowego.

4. Podsumowanie

Za pomocą dwóch metod otrzymano prędkości dźwięku w powietrzu . Metodą rezonansową zmierzono prędkość c=343.8 +- 1.8 [m/s], a metodą przesunięcia fazowego c=345.4 +- 7.0 [m/s]. Za pomocą obu wyznaczonych prędkości obliczono wykładniki adiabaty  =1.41+-0.06 .Wartość tablicowa  dla powietrza wynosi t=1.40. Jak widać metodą rezonansową otrzymano wartość  dokładniejszą niż metodą przesunięcia fazowego. Dzięki znajomości  można porównać wyznaczoną prędkość z wartością tablicową prędkości propagacji dźwięku w powietrzu (w tmperaturze 273 K). Prędkość c0 wyznaczono korzystając ze wzoru:

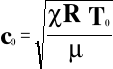
i wyniosła ona dla metody rezonansowej c01=331.7 [m/s] i c02=332.9 [m/s] dla metody przesunięcia fazowego. Błąd uzyskanego wyniku liczono ze wzoru: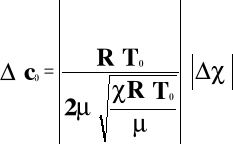
. Wyniósł on odpowiednio: c01=2.3 [m/s] , oraz c02=7.1 [m/s]. Wartość tablicowa c wynosi c0t=331 [m/s]. Porównanie ze sobą prędkości otrzymanych z pomiaru z wartością tablicową prowadzi do wniosku, że metoda rezonansowa jest dokładniejsza niż metoda przesunięcia fazowego - otrzymany wynik jest obarczony mniejszym błędem, a wartość prędkości jest dokładniejsza. Otrzymano za jej pomocą wartość: c01=331.7+-2.3 [m/s]. Odchyłka od wartości tablicowej wynosi: σ= c01- c0t/ c0t *100% =0.2 %. Używając metody przesunięcia fazowego otrzymano: c02=332.9+-7.1 [m/s]. W tym przypadku σ=0.6%. Warto zauważyć, że mimo użycia dwóch różnych metod otrzymano wyniki bardzo zbliżone do siebie. Fakt ten można wytłumaczyć tym, że pomiarów dokonywano na tych samych przyrządach, a szacowanie wyników przebiegało na liczbach tego samego rzędu.

---