Wyprowadzenie równań Hartree-Focka
Nie wprowadzamy parametrów wariacyjnych do funkcji falowej, ale energię traktujemy jako funkcjonał orbitali (czyli E=E(ψi))
(dla uproszczenia będziemy używali symbolu E zamiast Eel).
Należy obliczyć wariację energii (oznaczoną jako δE) spowodowaną wariacją orbitali. Każda zmiana orbitali ψ pociągnie za sobą zmianę wartości całek Ip, Jpq, Kpq, a tym samym zmianę energii wyrażonej równaniem
Wariacje całek Ip, Jpq, Kpq będziemy oznaczali odpowiednio przez δIp, δJpq i δKpq, a minimum energii E znajdziemy z warunku:
Pamiętamy, że zbiór orbitali ψ jest zbiorem ortonormalnym, a więc warunek ortonormalności (konieczność spełnienia tego warunku) ogranicza nam częściowo dopuszczalne zmiany orbitali. Warunek ortonormalności zbioru orbitali możemy zapisać jako:
![]()
dla p, q = 1, 2, 3, ..., n/2 ; przy czym δpq jest symbolem Kroneckera (równym 1 gdy p=q oraz równym 0 gdy p≠q)
Aby uwzględnić warunek ![]()
można zastosować metodę nieoznaczonych mnożników Lagrange'a.
W tym celu powyższe warunki zapiszmy jako Spq - δpq = 0, co musi być spełnione dla p, q = 1, 2, ..., n/2.
W metodzie nieoznaczonych mnożników Lagrange'a wprowadzamy dodatkowe współczynniki liczbowe εpq (mnożniki Lagrange'a) a powyższe warunki zapisujemy jako:
εpq ( Spq - δpq ) = 0
Załóżmy, że warunki ograniczające dotyczące całek Spq są spełnione.
Możemy wówczas napisać:
(ostatni człon możemy dodać do wyrażenia z prawej strony, gdyż zgodnie z wprowadzonymi warunkami człon ten jest równy zeru)
Równanie określające wariację δE przyjmie zatem postać:
(skorzystaliśmy z warunku, że wariacja z symbolu Kroneckera znika, co wynika z warunków ograniczających).
Obliczmy wariację całki Ip, czyli δIp przy założeniu, że wszystkie orbitale są rzeczywiste:
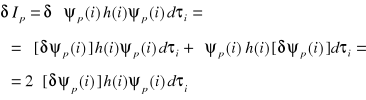
Wariacja całki Spq wynosi:
![]()
Wprowadzamy następnie dwa operatory:
operator kulombowski ![]()
oraz operator wymiany ![]()
, zdefiniowane przez określenie ich działania na orbital ψq(i) :
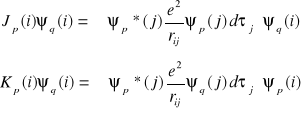
Wyrazimy następnie całkę kulombowską i całkę wymiany przez odpowiednie operatory:
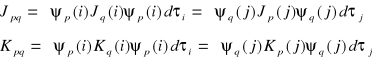
Wariując orbitale ψp będziemy stosować pierwszą postać tych operatorów, a wariując ψq będziemy stosować postać drugą:
Otrzymujemy:
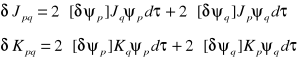
(opuściliśmy indeksy i, j numerujące elektrony)
uwaga: wymagane jest dokonanie wariacji zarówno orbitali ψp jak i orbitali ψq, gdyż operator kulombowski oraz operator wymiany zawierają (z definicji) funkcje ψp i ψq
Podstawiamy wyrażenia na: δIp, δSpq, δJpq i δKpq do równania
i otrzymujemy:
![]()
![]()
Powyższy wzór otrzymuje się przez proste podstawienie odpowiednich wariacji i wyłączenie czynnika 4∑ ∫ [δψp(i)]
Wiemy, że δψp(i) są dowolne, więc powyższe równanie jest spełnione jeżeli współczynniki przy δψp(i) znikają identycznie.
Mamy więc:
![]()
![]()
![]()
Zauważmy, że powyższy zapis jest tak naprawdę układem równań, gdyż pamiętamy, że dotyczy on współczynników przy δψp, a te dotyczyły wartości p = 1, 2, ... n/2. A zatem, gdybyśmy zapisali powyższe równanie najpierw dla p=1, później dla p=2, itd., to otrzymalibyśmy układ n/2 równań.
Jeżeli zdefiniujemy teraz operator ![]()
jako:
![]()
To wówczas możemy układ równań (w ramce) zapisać w zwięzłej formie:
gdzie p = 1, 2, 3, ..., n/2
Operator ![]()
nazywamy operatorem Focka:
![]()
Układ równań (dla p = 1, 2, 3, ..., n/2)
jest układem sprzężonych równań różniczkowo-całkowych. Rolę „niewiadomych” pełnią w tym układzie orbitale ψ, ale zauważmy, że występują one zarówno po prawej stronie znaku równości, jak i po lewej (m.in. w operatorach całkowych J i K).
Powyższy układ równań można sprowadzić do prostszej postaci. Przekształcenia unitarne (jak wiadomo z algebry liniowej) nie zmieniają wyznacznika (a nasza funkcja falowa jest właśnie wyznacznikiem). Możemy więc dokonać dowolnego przekształcenia unitarnego nie zmieniając wyznacznika (w naszym przypadku: funkcji). Dlatego mówi się, że wyznacznikowa funkcja falowa określona jest z dokładnością do transformacji unitarnej.
Wniosek: istnieje wiele równoważnych funkcji wyznacznikowych, którym odpowiada ta sama wartość energii. Funkcje te możemy otrzymywać (jedne z drugich) stosując transformacje unitarne (czyli działając na daną funkcję operatorem unitarnym
Dygresja: operator ![]()
nazywamy operatorem unitarnym, jeżeli zachodzi ![]()
, gdzie ![]()
jest operatorem sprzężonym do operatora ![]()
, natomiast ![]()
jest operatorem jednostkowym.
Mamy więc swobodę (której zasięgiem jest przekształcenie unitarne) w wyborze funkcji wyznacznikowej. Wybieramy więc taką postać funkcji wyznacznikowej, która sprowadzi nasz układ równań do prostszej postaci.
A zatem, wykonujemy taką transformację unitarną orbitali ψp, aby odpowiadająca tym orbitalom macierz współczynników εpq była diagonalna (czyli εpq=0 dla p≠q). Różne od zera pozostaną więc tylko te współczynniki εpq , dla których p=q (czyli εpp ). Możemy je zatem oznaczyć jako εpp albo εp.
Nasz układ równań przyjmuje zatem prostą postać:
(dla p = 1, 2, 3, ..., n/2 )
Powyższy układ równań nazywamy układem równań Hartree-Focka
Zauważmy, że operator Focka przypomina operator Hamiltona (również w sensie fizycznym), natomiast każde z równań Hartree-Focka przypomina jednoelektronowe równanie Schrödingera
Orbitale Hartree-Focka (kanoniczne). Energie orbitalne
Zauważmy, że orbitale ψp są funkcjami własnymi operatora Focka,
a wartościami własnymi są współczynniki liczbowe εp
Wobec tego, można się spodziewać, że współczynniki εp będą miały związek z energią. Rzeczywiście, liczby te nazywane są energiami orbitalnymi (np. dla i-tego elektronu opisywanego orbitalem ψp(i), energia orbitalna wynosi εp).
Energię orbitalną εp można interpretować jako energię elektronu poruszającego się w polu jąder i w uśrednionym polu potencjału wszystkich pozostałych elektronów.
Orbitale ψp występujące w równaniach Hartree-Focka nazywamy orbitalami Hartree-Focka (lub orbitalami kanonicznymi).
Energie orbitalne εp są po prostu wartościami średnimi odpowiednich operatorów Focka, gdyż ![]()
Warto jednak pamiętać, że całkowita energia elektronowa nie jest sumą energii orbitalnych. Jest tak dlatego, że energia orbitalna każdego elektronu obejmuje uśrednioną energię oddziaływania tego elektronu z wszystkimi pozostałymi elektronami. Tak więc energia oddziaływania między każdą parą elektronów liczona jest dwukrotnie.
Metoda rozwiązywania równań Hartree-Focka
Widzimy więc, że procedura wariacyjna (analogiczna do tej, którą stosujemy np. w metodzie Ritza), mająca na celu znalezienie orbitali odpowiadających najmniejszej możliwej wartości energii, prowadzi w efekcie do układu równań Hartree-Focka (jest to układ sprzężonych równań różniczkowo-całkowych).
![]()
Pamiętamy, że niewiadomymi w tych równaniach są orbitale ψp
i to właśnie znalezienie tych orbitali jest naszym zadaniem.
Występujące w operatorze Focka operatory ![]()
, ![]()
zależą od wszystkich orbitali, a więc operator Focka zależy od wszystkich orbitali.
Dochodzimy zatem do (pozornego) paradoksu:
aby obliczyć orbitale (co jest naszym celem), musimy zbudować najpierw operator Focka, a żeby to zrobić, musimy znać wszystkie orbitale. Czyli aby obliczyć orbitale musimy znać orbitale!
Okazuje się, że ten pozornie niemożliwy do rozwiązania problem można jednak rozwiązać. Stosuje się do tego metodę iteracyjną.
Postępowanie w metodzie iteracyjnej jest następujące:
1. Zakładamy pewne startowe orbitale ψ1, ψ2, ψ3, ..., ψn/2 . Ponieważ są to orbitale startowe oznaczmy je dodatkowym symbolem (0). Mamy więc orbitale startowe: ψ1(0), ψ2(0), ψ3(0), ..., ψn/2(0)
2. Stosując te orbitale budujemy operatory Focka (obliczając odpowiednie potencjały).
3. Wstawiamy zbudowane z orbitali ψ1(0), ψ2(0), ψ3(0), ..., ψn/2(0) operatory (ściślej: obliczone potencjały) do równań Hartree-Focka.
4. Rozwiązujemy otrzymane równania Hartree-Focka uzyskując wyniki: nowy zbiór orbitali ψ1(1), ψ2(1), ψ3(1), ..., ψn/2(1) (oznaczonych teraz symbolem (1), zestaw energii orbitalnych ε1(1), ε2(1), ..., εn/2(1) oraz całkowitą energię elektronową E(1).
5.Sprawdzamy, czy uzyskane w punkcie No4 orbitale ψ1(1), ψ2(1), ..., ψn/2(1) oraz całkowita energia elektronowa są identyczne, jak odpowiednie wielkości obliczone z orbitali, które zostały użyte do ich obliczenia (czyli w tym przypadku ψ1(0), ψ2(0), ψ3(0), ..., ψn/2(0)).
Jeżeli oba zestawy są identyczne - mówimy, że doszło do samouzgodnienia i kończymy procedurę (gdyż znamy już dokładne, samouzgodnione orbitale).
Jeżeli oba zestawy nie są identyczne - wykonujemy obliczenia dalej: znowu używamy orbitali (tym razem zbioru ψ1(1), ψ2(1), ..., ψn/2(1) ) do konstrukcji operatorów Focka, po czym rozwiązujemy równania Hartree-Focka. Uzyskujemy kolejny zestaw orbitali (ψ1(2), ψ2(2), ..., ψn/2(2), energii orbitalnych ε1(2), ε2(2), ..., εn/2(2), jak również całkowitą energię elektronową E(2). Wyniki porównujemy z poprzednimi (sprawdzając, czy doszło do samouzgodnienia).
Postępowanie iteracyjne kontynuujemy tak długo, aż dojdzie do samouzgodnienia wyników, to znaczy, aż do momentu, gdy orbitale uzyskane w wyniku rozwiązania równań Hartree-Focka nie będą się różniły od orbitali zastosowanych do konstrukcji tych równań.
Metodę Hartree-Focka nazywamy metodą pola samouzgodnionego
(ang. Self-consistent field, SCF ).
Techniczna metoda (opracowana przez Roothaana) rozwiązywania równań Hartree-Focka.
Jednym z etapów postępowania w metodzie SCF jest rozwiązanie równań Hartree-Focka (dla danych orbitali). Jak się okazuje, jest to zadanie bardzo trudne (nawet przy użyciu metod numerycznych i bardzo szybkich maszyn cyfrowych).
Roothaan zaproponował przybliżoną metodę rozwiązywania równań Hartree-Focka na drodze konstrukcji analitycznych przybliżeń do orbitali Hartree-Focka. Mianowicie, zakładamy orbitale ψp w postaci kombinacji liniowych pewnych znanych funkcji χ, nazywanych funkcjami bazy.
Czyli każdy orbital ψp przyjmuje postać:
![]()
Po wstawieniu takiej formy orbitali do układu równań Hartree-Focka okazuje się, że poszczególne równania przestają być skomplikowany-mi równaniami różniczkowymi przechodząc w znacznie prostsze równania algebraiczne. Po rozwiązaniu tych równań otrzymujemy wyniki w postaci zestawu współczynników liczbowych cpi.
Ponieważ funkcje χi znamy, mamy natychmiast poszukiwane orbitale Hartree-Focka ψp.
Uwaga No1: Metoda Hartree-Focka w połączeniu z techniką Roothaana jest nazywana metodą Hartree-Focka-Roothaana (HFR).
Uwaga No2: Metoda HF jest jedną z najpopularniejszych metod stosowanych współcześnie w chemii kwantowej (często w połączeniu z innymi metodami uwzględniającymi tzw. korelację elektronową).
Uwaga No3: Metodę HF stosuje się prawie zawsze w schemacie Roothana (czyli stosuje się metodę HFR).
Uwaga No4: Metoda Hartree-Focka prowadzi do najlepszej możliwej do uzyskana energii w ramach przybliżenia jednoelektronowego a także do najlepszych orbitali możliwych do uzyskania w ramach tego przybliżenia.
Uwaga No5: Intuicja współczesnych chemików (np. pojęcie orbitali) opiera się przede wszystkim na pojęciach określonych przez metodę Hartree-Focka i przybliżenie jednoelektronowe.
125
![]()
![]()
![]()
![]()
![]()
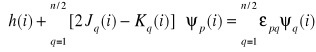
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
wykladChK-03, Chemia UŁ, teoretyczna wykład
wykladChK-10, Chemia UŁ, teoretyczna wykład
wykladChK-11, Chemia UŁ, teoretyczna wykład
wykladChK-15, Chemia UŁ, teoretyczna wykład
wykladChK-13, Chemia UŁ, teoretyczna wykład
wykladChK-07, Chemia UŁ, teoretyczna wykład
wykladChK-14, Chemia UŁ, teoretyczna wykład
wykladChK-04, Chemia UŁ, teoretyczna wykład
wykladChK-09, Chemia UŁ, teoretyczna wykład
wykladChK-05, Chemia UŁ, teoretyczna wykład
wykladChK-01, Chemia UŁ, teoretyczna wykład
wykladChK-02, Chemia UŁ, teoretyczna wykład
Prawo konkurencji wykład 7 - 04.12, WPiA UŁ, Prawo ochrony konkurencji i konsumentów (T. Ławicki)
prawo konkurencji wykład 8 - 11.12, WPiA UŁ, Prawo ochrony konkurencji i konsumentów (T. Ławicki)
wyklad 1 1 2008, CHEMIA UŁ, 3 rok, Fizyczna, różne
Prawo konkurencji wykład 7 - 04.12, WPiA UŁ, Prawo ochrony konkurencji i konsumentów (T. Ławicki)
Wykład 12 Chemia Organiczna, grupy funkcyjne, klasy związków 5fantastic pl
CHEMIA 12, Chemia fizyczna AGH laborki, lab 12
temat 12, chemia wody-w-
więcej podobnych podstron