Politechnika Świętokrzyska
Wydział Mechatroniki i Budowy Maszyn
Przedmiot: Mechanika doświadczalna
Ćw. Nr 5 Temat: Całka J - pomiar metodą wielu próbek .
Wykonał: Łukasz Skiba	Grupa: 302	Data: 3.12.2008	Prowadzący: dr inż. Lis Zbigniew	Ocena:

1. Wstęp.

Kryterium pękania wykorzystujące pojęcie współczynnika intensywności naprężeń jest wyłącznie prawdziwe dla materiałów kruchych, dla których praktycznie nie obserwuje się odkształceń plastycznych. Jak wykazano powyższe kryterium dopuszcza co najwyżej niewielka strefę plastyczną przed frontem pęknięcia, której długość r_p jest mniejsza niż jedna setna długości pęknięcia a. W innym przypadku materiał ma skłonność do pękania, w którym ciągliwy charakter tego procesu zaczyna odgrywać istotną rolę aż do całkowitej dominacji nad mechanizmem pękania kruchego. Wielkość strefy plastycznej staje się na tyle duża, że nie można już założyć, że materiał jest liniowo sprężysty. prawo Hooka przestaje obowiązywać i obliczenia należy wykonać stosując związek konstytutywny dla ciał sprężysto-plastycznych lub plastycznych. W zakresie plastycznym zależność pomiędzy składowymi tensorów odkształcenia i naprężenia nie jest liniowa. Co więcej, bardzo często naprężenia zależą od sposobu w jaki obciążamy próbkę (zależą od historii obciążenia). Rozwiązanie tak zwanego problemu brzegowego staje się znacznie trudniejsze i niełatwo go uzyskać w postaci zamkniętej. Rozwiązanie to nazywa się dziś rozwiązaniem HRR. problem rozwiązano dla materiału nieliniowo sprężystego opisanego związkiem konstytutywnym Ramberga-Osgooda.

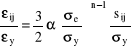
,n - stałe materiałowe;
- naprężenia efektywne;
- granica plastyczności;
- współrzędne dewiatora naprężeń.

Dla takiego materiału rozwiązanie HRR ma postać:

,

.

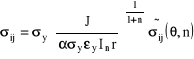
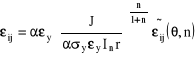
I_n- funkcja n zależy od tego czy analizujemy p.s.n czy p.s.n.

,
-funkcja zależna od wykładnika n i kąta
określającego połażenie wybranego punktu względem płaszczyzny szczeliny.

Funkcje te maja uniwersalny charakter gdyż nie zależą od geometrii elementu. Naprężenia i odkształcenia są proporcjonalne do:

,
.

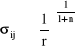
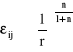
są osobliwe (wzrastają do nieskończoności gdy r
0). Gdy materiał jest liniowo sprężysty to wówczas n=1 naprężenia i odkształcenia dążą do nieskończoności, maja osobliwość
. Gdy n=
to mamy do czynienia z ciałem doskonale plastycznym (nie umacniającym się) i wówczas naprężenia są skończone przed frontem szczeliny a odkształcenia mają osobliwość 1/r. Aby móc ocenić jak szybko naprężenia i odkształcenia zmierzają do nieskończoności należy znać amplitudę tej osobliwości, którą w tym przypadku oznaczono przez J i nazwano całką J.

Własności całki J.

-jest amplitudą osobliwego pola naprężenia odkształceń przed frontem szczeliny,

-odpowiada ilości energii uwolnionej z elementu przy przyroście szczeliny o długość da,

-jest niezmiennicza od konturu całkowania (występują ograniczenia).

Biorąc pod uwagę te cechy można postulować kryterium pękania w postaci:

J_I (dł szczeliny a, obciążenia zewnętrzne, parametry geometryczne elementu) =J_IC

J_IC może być uznane za stalą materiałową gdy badany element próbka znajduje się w p.s.o. Stanie się tak jeżeli będą spełnione poniższe warunki:

b oraz B oraz a >
, gdzie a=25 dla próbek z prawda zginania i a=175 dla próbek rozciąganych.

Istota tej metody polegania tym, że jej twórcy (Landes, Begeley) zaproponowanie kilku w miarę możliwości jednakowych próbek (co najmniej pięciu), łącznie z pęknięciem zmęczeniowym przed frontem naciętego karbu. Następnie każdą próbkę należy obciążyć na maszynie wytrzymałościowej do innej wartości przemieszczenia punktu przyłożenia siły
. W domyśle każdej wartości
odpowiadać powinna inna wartość przyrostu długości pęknięcia
. Następnie każdą próbkę odciążamy wkładając do pieca (ok 300⁰)w celu zabarwienia przełomu. Po wystudzeniu próbkę doładujemy i za pomocą mikroskopu laboratoryjnego dokonujemy zarówno początkowej długości pęknięcia a₀ jak i b₀ oraz końcowej długości pęknięcia a_k. W ten sposób potrafimy obliczyć przyrost długości pęknięcia
i oznacza kolejny numer próbki. Kolejnym krokiem jest obliczenie pola powierzchni A_i pod krzywą P-
. Zmierzymy więc ilość energii, która została dostarczona do próbki od momentu początku jej obciążenia do momentu przerwania próby.

Wartości A_i, (b₀)_i, B podstawiamy do wzoru:

dla próbek typu kompakt; b₀- dł niepękniętego odcinka próbki przed frontem pęknięcia

dla próbki trójpunktowo zginanej.

Obliczając wartość całki J_i. W efekcie otrzymamy kilka par współrzędnych par punktów na wykresie

Na wykresie poza kilkoma punktami (J_i,
) wrysowano kilka linii Linia prosta wychodząca z początku układu współrzędnych nazywana jest linią stępienia J=(s_y+s_m)Da. Linia stępienia symuluje proces stępienia ostrej początkowo szczeliny. Po wrysowaniu lini stępienia rysuje się dwie ograniczające, równoległe do tej pierwszej i mające swój początek w odległości Da=0.15mm i 1.5mm. Linie te ograniczają ilość „ważnych” punktów pomiarowych> Punkty J_i,Da, które znalazły się na zewnątrz obszaru ograniczającego przez linię ograniczające eliminuje się z dalszej analizy. Liczba pozostałych punktów powinna być nie mniejsza niż cztery. W oparciu o te punkty wykreślamy prostą regresji. prostą tą nazywamy „linią R”. Następnie wrysowujemy dwie linie pomocnicze dające wartość J większe o 35 i mniejsze o 25% w stosunku do linii R. Punkt przecięcia linii R z linią stępienia określi nam J_IC wtedy i tylko wtedy gdy spełniony zostanie warunek:

b oraz B oraz a >

2. Schemat układu pomiarowego.

3. Wyniki pomiarów i obliczeń.

[N/mm]

gdzie:
= 2 - dla próbki trójpunktowo zginanej

A - pole pod krzywą P-D

b_o = W - a_o - dł. niepękniętego odcinka próbki

B - grubość próbki

Wykres całki J w funkcji Da sporządzony w oparciu o pomiary i obliczenia sporządzone przez pozostałe grupy laboratoryjne.

Lp		B [mm]	W [mm]	ao [mm]	da [mm]	A [Nmm]	J [N/mm]
1	SR15_AN	12,46	24,92	12,540	0,450	18768	243,3376
2	Cw11_MG	12,5	25,01	12,956	0,452	19370	257,1097
3	SR08_AN	12,44	24,97	13,030	0,811	20310	273,4735
4	WT09_AN	12,45	24,95	12,550	0,540	23310	301,9821
5	WT08_AN	12,45	24,96	12,470	0,825	28717	369,3493
6	SR13_JG	12,5	24,98	13,096	1,280	32107	432,2639
7	SR16_DI	12,46	24,98	12,349	1,403	33641	427,5069
8	PN15_MG	12,49	25,07	13,296	1,595	36417	495,2765
9	PN13_ZL	12,58	24,97	12,633	2,136	46344	597,2186
10	PN09_DI	12,47	24,96	13,290	2,350	44595	612,8848
11	Cw13_DI	12,45	25	13,250	3,380	49449	676,0523

Wartość J odczytana na podstawie wykresu wynosi około 205 [N/mm].

5,31 < a, B, b

Warunek spełniony, wiec

4. Wnioski.

W powyższym doświadczeniu wyznaczaliśmy całkę J_IC, za pomocą metody wielu próbek, zgodnie z zaleceniami PN. Pomiar został dokonany prawidłowo gdyż liczba punktów w zakresie od 0,15 do 1,5 mm Δa oddzielone liniami równoległymi do linii stępienia wynosi więcej niż 4 punkty jak przewiduje PN.

Błędy, jakie mogły mieć zasadniczy wpływ na otrzymany wynik to:

• błędy pomiaru wielkości geometrycznych próbek:

• błędy wyznaczenia nie pękniętego odcinaka próbki i wielkości przyrostu długości szczeliny da;

• błędy spowodowane wygładzaniem wykresu P(U), co w konsekwencji miało wpływ na wartość całki, czyli pola powierzchni pod wykresem;

• błąd wyznaczenia linii regresji.

---