Nowakowski Sławomir		Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn		Laboratorium z mechaniki doświadczalnej
Temat: Wyznaczanie całki metodą zmiany podatnosci
Grupa 32 b	Data: 05.01.01		Ocena:		Podpis:

1. Cel ćwiczenia.

Celem ćwiczenia jest praktyczne zapoznanie się z metodami pomiaru przyrostu długości szczeliny. Badanym materiałem jest stal 40HMNA. Badanie zostało przeprowadzone przy użyciu hydropulsacyjnej maszyny wytrzymałościowej MTS.

Schemat blokowy układu pomiarowego.

2. Wstęp teoretyczny.

Amplitudę osobliwych naprężeń i odkształceń dla ciał nieliniowych nazywamy całką J.

Całka J jest amplitudą naprężeń i odkształceń przed frontem szczeliny w ośrodku nie linowym wg. prawa Ramberga- Osgooda.

Ogólna postać tej całki

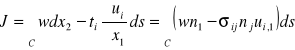
Całka J jest nie zmiennicza od drogi całkowania

Należy pamiętać również o ograniczeniach w stosunku do całki J.

Całka jest niezmiennicza od drogi całkowania dla ciał liniowych i nie liniowo sprężystych oraz dla ciał plastycznych wg. teorii plastyczności. W ostatnim przypadku tylko dla szczelin stacjonarnych. Całka J nie jest niezmiennicza od drogi całkowania dla zagadnień dynamicznych.

Całka J jest równoważna różnicy energii potencjalnych dwóch prawie takich samych, identycznie obciążonych próbek różniących się jedynie długością szczeliny o infinitezymalną długość da.

Całka J ma miano (Nxm)/m²= N/m, gdyż zmianę energii potencjalnej obliczamy na jednostkowy przyrost powierzchni szczeliny.

J_1c może być uznane za stałą materiałową gdy badany element znajduje się w p.s.o. Stanie się tak gdy zostanie spełniona nierówność:

b oraz B oraz a>

gdzie α= 25 dla próbek w których występuje przewaga zginania, α=175 dla próbek rozciąganych.

Aby doświadczalnie wyznaczyć wartość całki J_1cnależy rozstrzygnąć dwie sprawy:

• dostarczyć wzór na obliczenie całki J w oparciu o dane otrzymane z eksperymentu,

• oszacować moment w którym zacznie wzrastać pęknięcie.

Wzór na obliczenie całki J w oparciu o dane otrzymane z eksperymentu:

gdzie:

η=2 dla trójpunktowego zginania

b_o- długość niepękniętego odcinka próbki przed frontem pęknięcia

B- grubość próbki

A- sumaryczna ilość energii zmagazynowanej odwracalnie zmagazynowanej w próbce A_spr oraz dysypowanej na odkształcenia plastyczne A_pl, oznaczają powierzchnie pod krzywą P-Δ.

Istniej kilka metod i technik pomiarowych pozwalających na oszacowanie momentu w którym zacznie wzrastać pęknięcie np.

1. metoda wielu próbek

2. metoda jednej próbki -technika zmiany podatności

3. metoda jednej próbki - technika spadku potencjału.

3. Schemat stanowiska.

4. Wyniki pomiarów i obliczeń.

Materiał próbki: 40HMNA.
Próbka trój punktowo zginana, nr L2.
Własności wytrzymałościowe		Geometria próbki
Re [MPa]	Rm [MPa]	ao [mm]	B [mm]	W [mm]	b=W-a0 [mm]
1265	1387	12.449	20.01	24.957	12.493

Metoda zmiany podatności.

Podatność obliczamy ze wzoru :

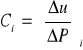
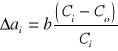
gdzie : b=W-a_o

C_o - podatność zerowa

Co=0,0247 [mm/kN] - podatność wyliczona na podstawie punktów leżących na liniowej części wykresu P=f(u)

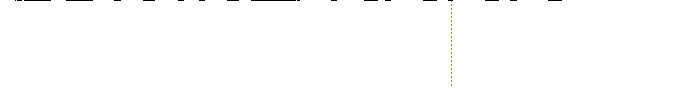
gdzie: B=20,01[mm] ; W=24,957[mm] ; S=100[mm] ; a_i=a_o+ Δa_i [mm] ;

ν=0.3 ; E=2.15*10⁵ [Mpa]

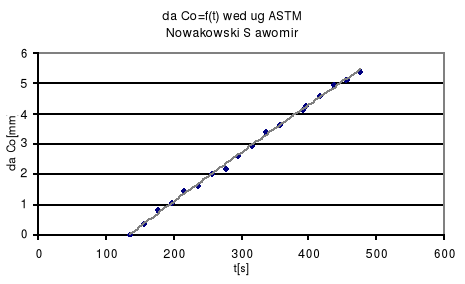
Wyniki pomiarów:

Wykres obciążania i odciążania próbki zawierającej pęknięcie i zmiany podatnoasci

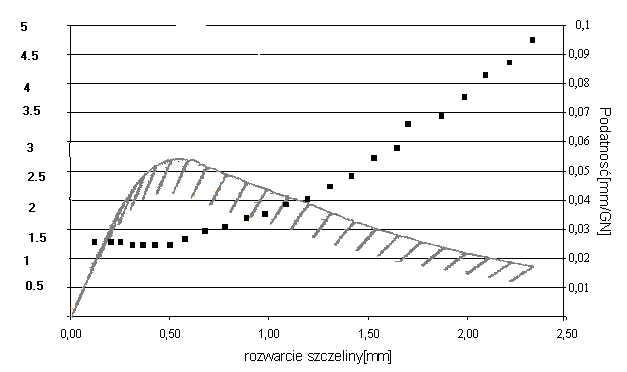
wraz z wzrastającym przemieszczeniem.

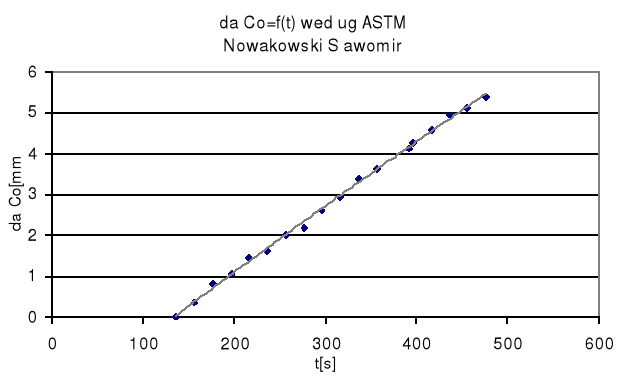
Wyniki uzyskane przy użyciu programu Fracture:

co	A1	A2	A1+A2	J[N/mm]
0,0283	1,059	21,949	23,007	16,8123
0,0271	6,621	65,08	71,7	49,11892
0,0265	8,755	119,769	128,524	67,89337
0,0269	25,694	165,824	191,518	93,28081
0,0265	39,422	216,166	255,588	123,262
0,0265	83,275	247,612	330,886	154,2369
0,0275	124,025	290,638	414,662	185,131
0,0281	214,312	280,488	494,8	216,124
0,0296	287,542	279,139	566,68	250,6462
0,03	389,223	236,232	625,454	279,3347
0,0317	472,87	244,423	717,293	306,7233
0,0329	550,168	237,849	788,017	332,8662
0,0346	634,68	236,365	871,044	357,7459
0,0355	717,802	242,651	960,452	383,3283
0,0372	785,109	243,509	1028,617	403,0618
0,0376	873,282	200,394	1073,676	425,2168
0,0389	958,686	153	1111,686	444,8716
0,042	1014,879	149,313	1164,192	464,161
0,0455	1123,64	87,25	1210,889	499,1685
0,0488	1158,019	92,258	1250,277	514,275
0,0502	1198,065	94,604	1292,669	527,3927

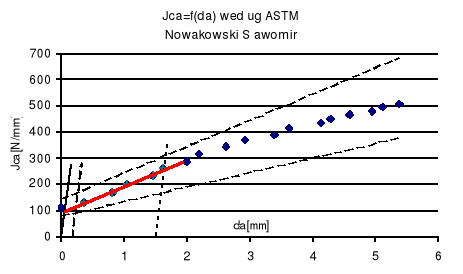
Wykres wyznaczania wartości J1c w oparciu o uzyskane wyniki z doswiadczenia.

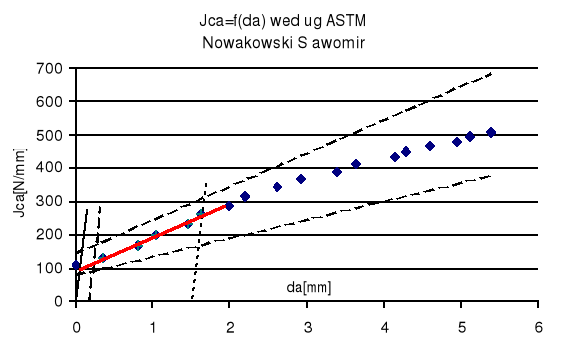
J_Q=93,335 [N/mm]

b oraz B oraz a >

b=12,493mm

B=24,957mm

a=12,449mm

=25

b,B,a>2,596mm warunek spełniony

5. Wnioski .

Przeprowadzone doświadczenie miało na celu wyznaczenie momentu inicjacji oraz wyznaczenie przyrostu długości szczeliny. Wielkości te są niezbędne dla określenia odporności materiałów sprężysto - plastycznych na pękanie.

Próbę doswiadczalnego wyznaczenia całki J można uznać za ważną, gdyż pomiędzy liniami ograniczającymi znalazło się pięć punktów , a warunek dotyczący geometrii próbki został spełniony.

Wzmacniacz Micro

MTS Profiler

Mostek

tensom.

Czujnik

rozwarcia pęknięcia

Czujnik przem. trawersy

obciążenie

Układ obciążający

Moduł

A/C

PC

---