POLITECHNIKA ŚWIĘTOKRZYSKA W KIELCACH
LABORATORIUM MECHANIKI DOŚWIADCZALNEJ
Nr Ćwiczenia:	Temat: Pomiar rozwarcia wierzchołka pęknięcia (RWP), kąta rozwarcia pęknięcia (KRP) i kąta rozwarcia wierzchołka pęknięcia (KRWP).	Wykonała: Milena Parzych
Data wykonania: 07.01.00	Data oddania: 21.01.00	Ocena:

1.Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z metodyką:- rozwarcia wierzchołka pęknięcia w oparciu o normę, jak również przy wykorzystaniu dwóch ekstensometrów, by nie przyjmować r jako wartości stałej, - kąta rozwarcia pęknięcia oraz kśt rozwarcia wierzchołka pęknięcia według podejścia lokalnego i globalnego.

2.Wstęp teoretyczny:

Przed momentem inicjacji pęknięcia następuje stępienie plastyczne szczeliny ostrej. W wyniku tępienia następuje rozwarcie szczeliny do wartości przemieszczenia w jej umownym wierzchołku.

Wells przedstawił przybliżoną analizę rozwarcia wierzchołka pęknięcia dla materiałów plastycznych. Motywacją był związek między RWP i współczynnikiem intensywności naprężeń K dla uplastycznienia bliskiego zasięgu. Jeżeli założymy, że przed wierzchołkiem szczeliny istnieje strefa plastyczna o promieniu r, to w efekcie rozwarcia powierzchni szczeliny w pobliżu jej wierzchołka można obliczyć w różny sposób. Jeden z nich to model Irwina. Założono w nim, że na wskutek istnienia strefy plastycznej wierzchołek szczeliny przesunięty zostaje ( umownie ) w okolice jej środka. Wówczas przemieszczenie u obliczymy ze wzoru:

μ - moduł ściskania,

ν - współczynnik Pissona.

Innym ciekawym modelem jest model Dugdela lub model pasma plastycznego (zaletą modelu jest wyeliminowanie osobliwych naprężeń przed wierzchołkiem szczeliny). Plastyczną strefę o kształcie klinowym przed wierzchołkiem szczeliny modelowano przez zastąpienie jej jednowymiarowym obszarem, wewnątrz którego panuje jednorodne naprężenie ściskające o wartości równej granicy plastyczności. Szczelinę wydłuża się o długość strefy plastycznej.

Modele Irwina czy Dungala w sposób jednoznaczny określają miejsce, w którym obliczono RWP. Dla innych modeli lub przy wykorzystaniu metody elementów skończonych miejsce, w którym oblicza się RWP wyznaczone jest jako przecięcie się prostych zaczepionych w fizycznym wierzchołku szczeliny z jej profilem, przy czym proste te wykreśla się pod kątem + lub - ¾ π w stosunku do osi.

Obliczenia RWP można dokonać za pomocą wzoru wykorzystując koncepcje zastosowania dwóch ekstensometrów. Wykorzystanie tej metody pozwoli na obliczenie r a nie przyjmowanie jego wartości ( wykorzystano analizę trójkątów podobnych ). Rejestrując sygnały z dwóch czujników rozwarcia pęknięcia RP1 i RP2 oraz mierząc dwa wymiary k i a rozwarcie wierzchołka pęknięcia obliczymy z poniższego wzoru:

Korzystając z tej metody możemy określić kąt rozwarcia pęknięcia oraz kąt rozwarcia wierzchołka pęknięcia, za pomocą wzorów:

Kąt rozwarcia i kót rozwarcia wierzchołka pęknięcia mierzone są w sposób pośredni, wykorzystując sygnały: zmiany potencjału, zmiana siły obciążającej, przemieszczenie punktu przyłożenia siły oraz rozwarcie szczeliny mierzone dwoma ekstensometrami RP1 i RP2.

• 
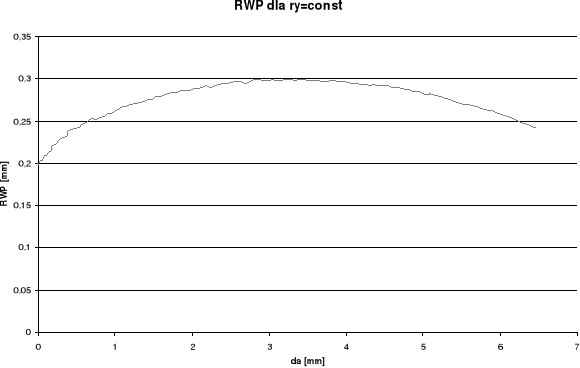
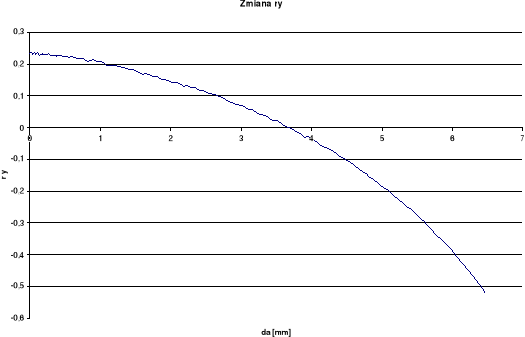
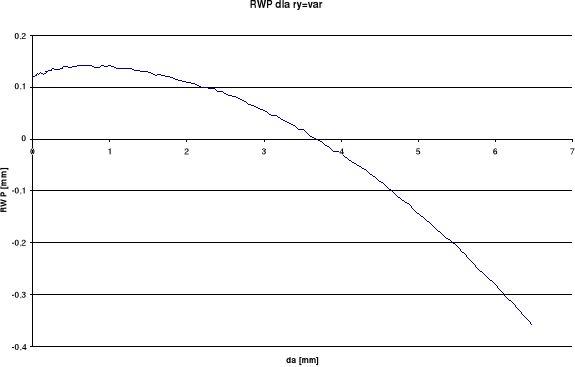
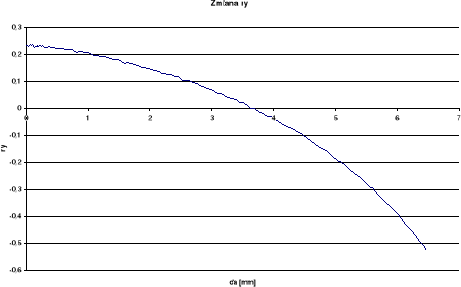
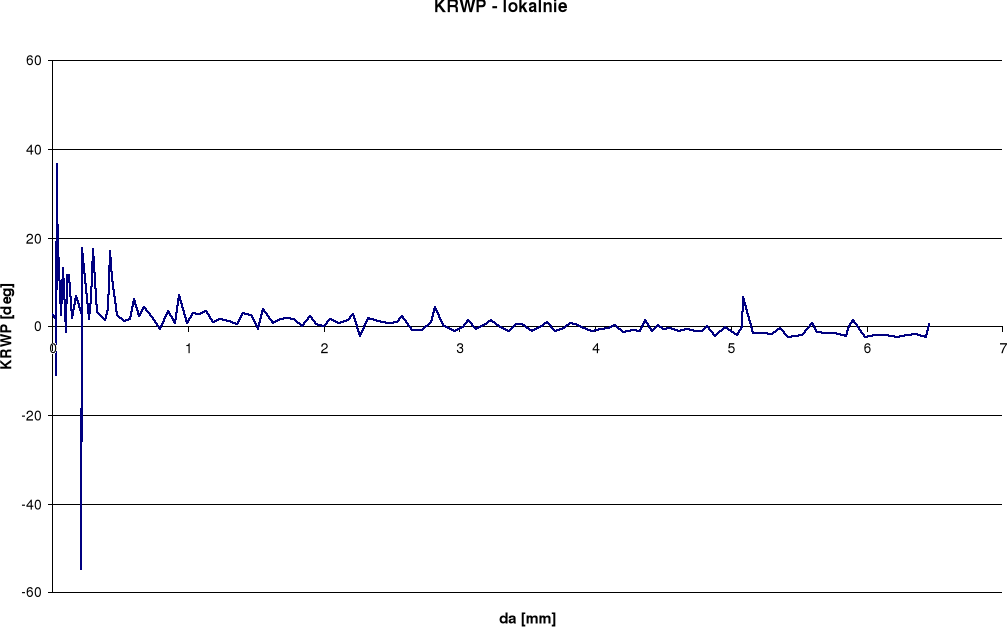
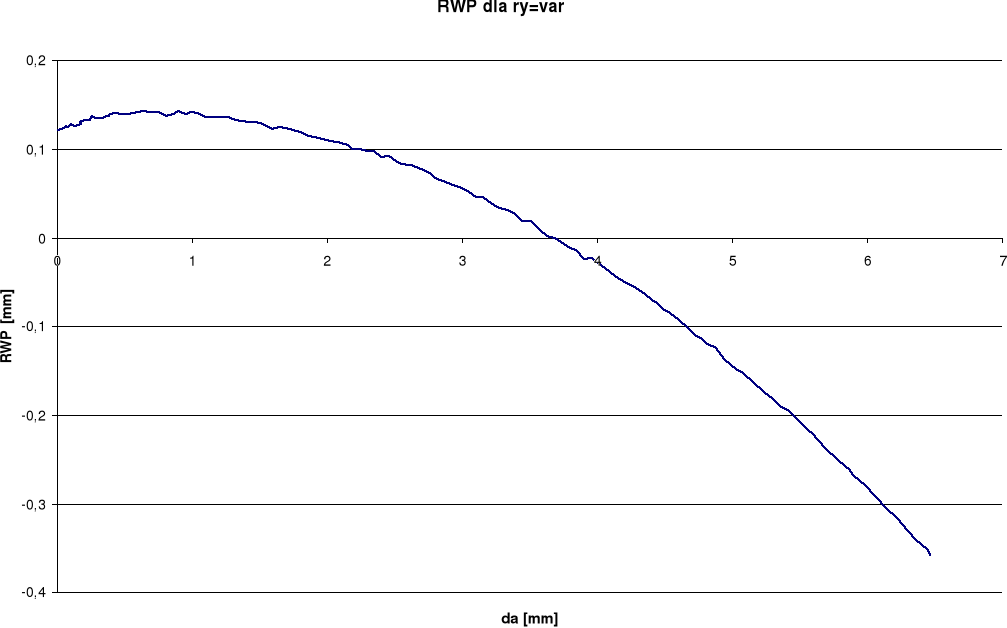
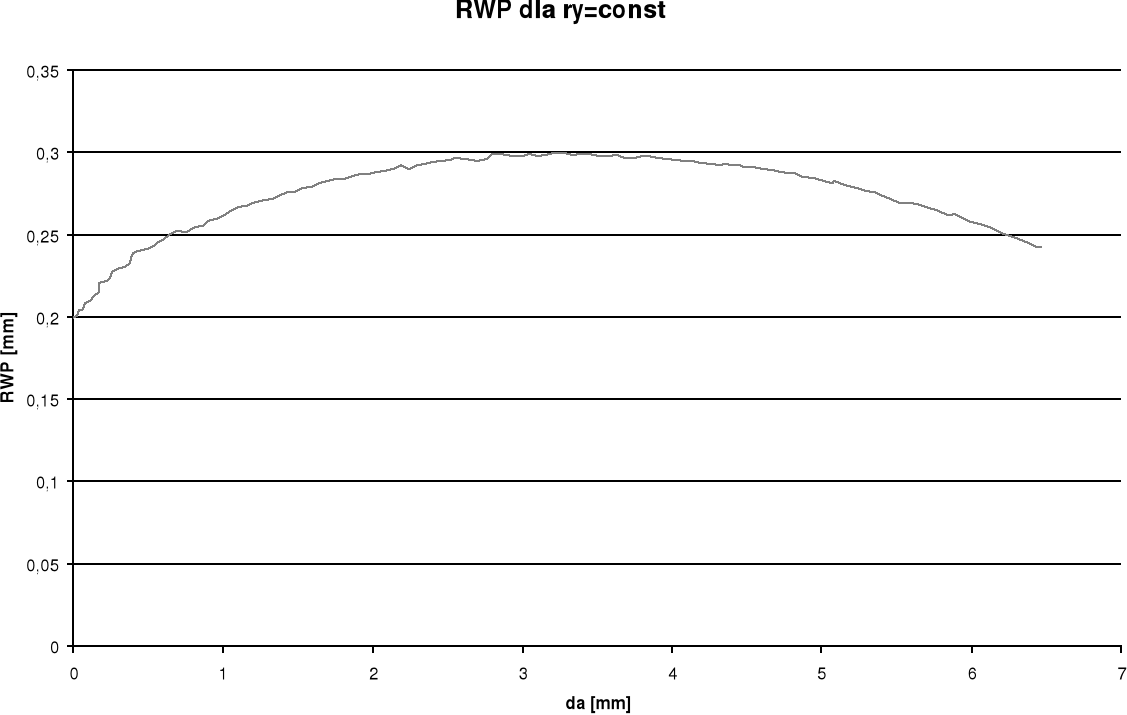
  RWP

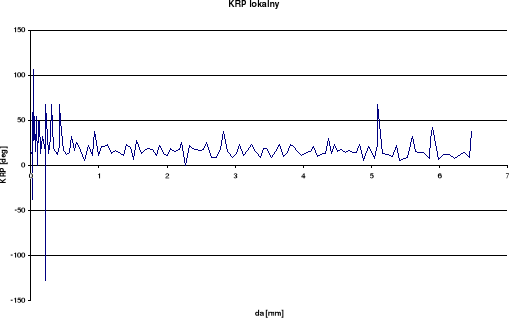
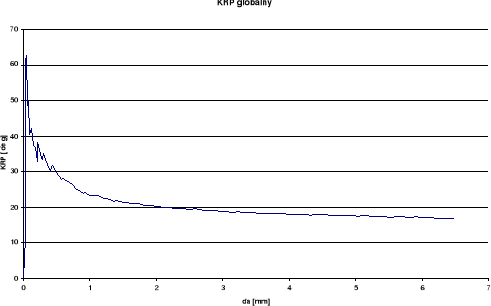
• KRP

• 
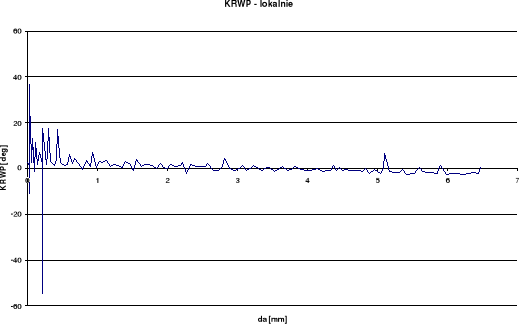
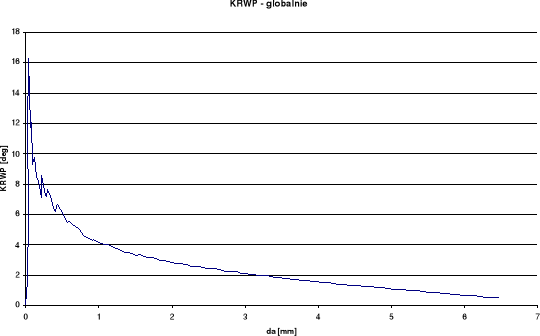
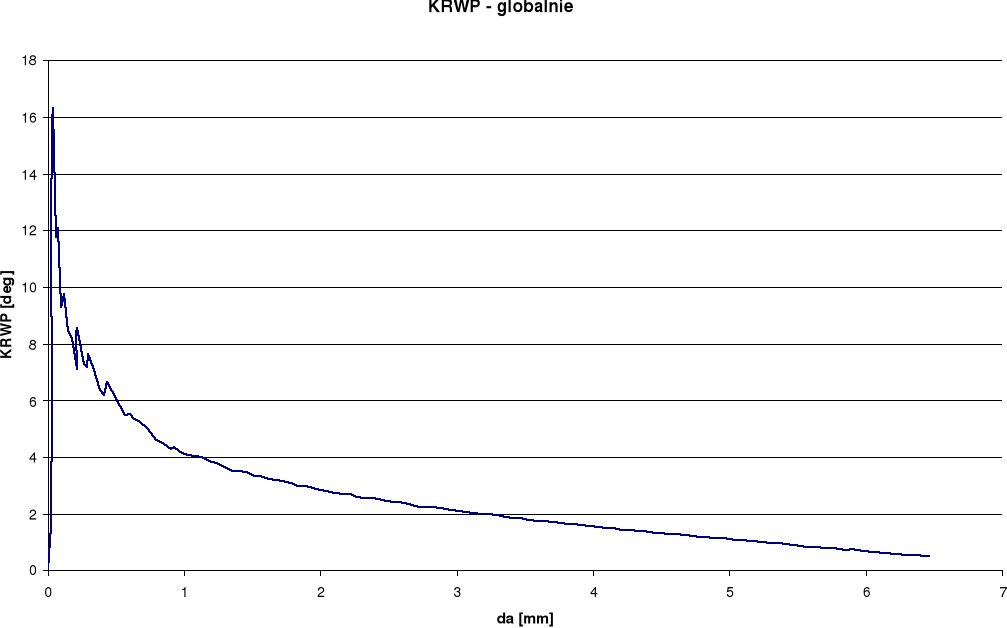
  KRWP

Wnioski:

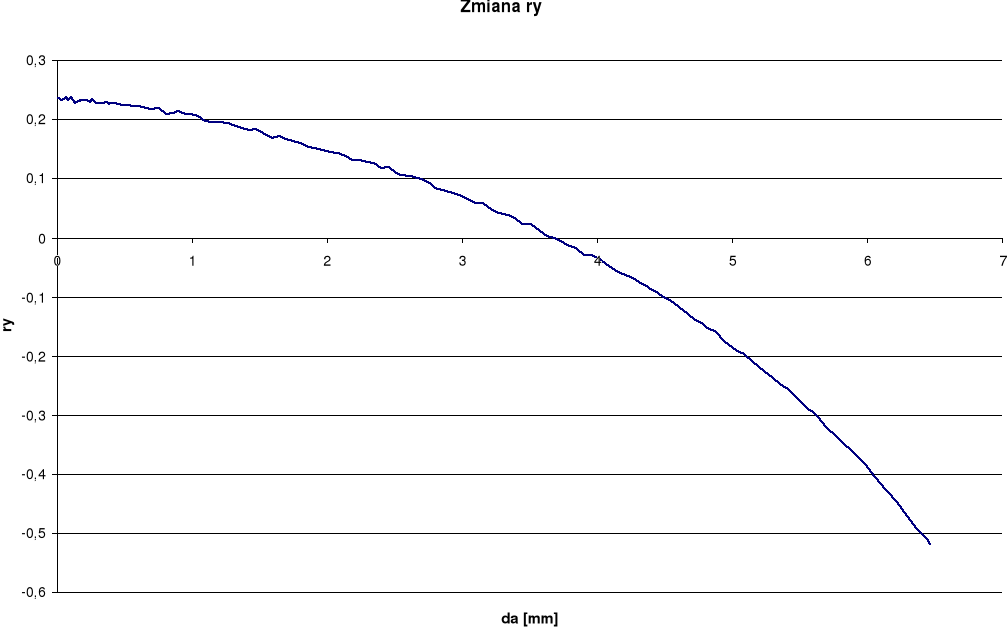
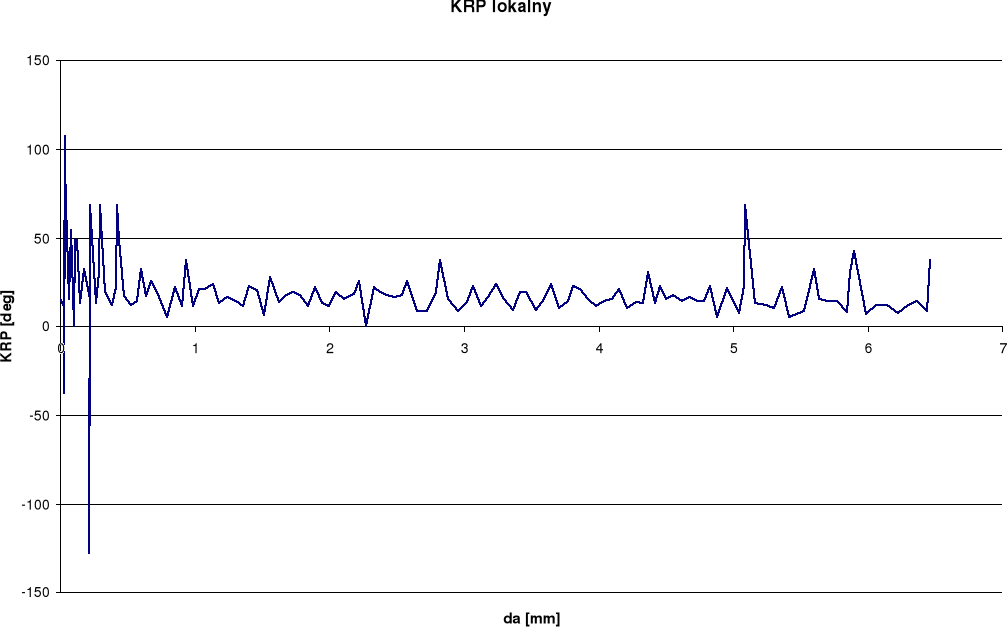
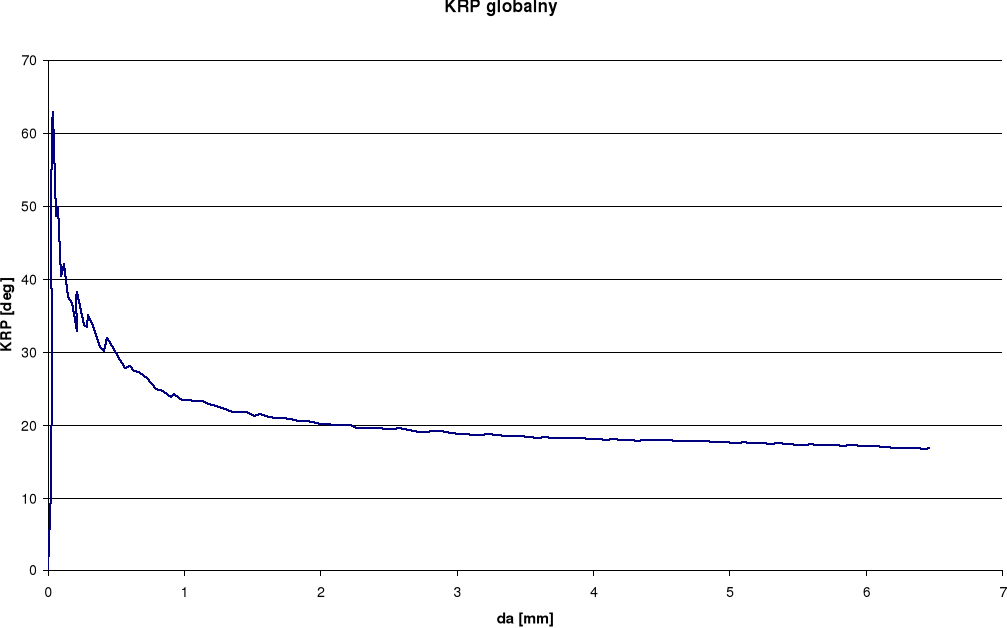
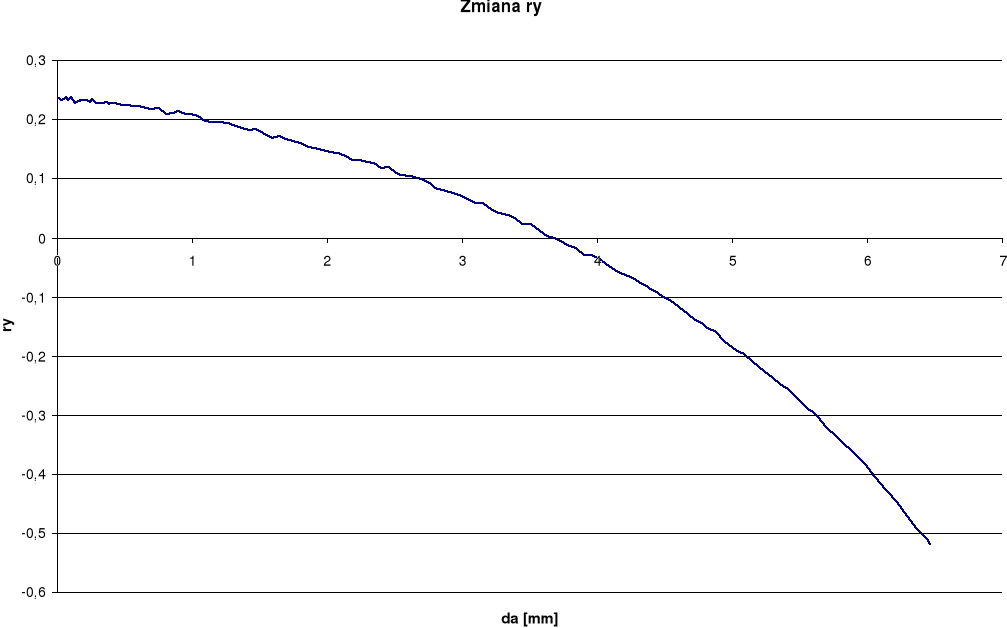
Wykresy otrzymane dla pomiaru rozwarcia wierzchołka pęknięcia (RWP) wykazują w późniejszym okresie spadek rozwarcia przy wzroście długości szczeliny. Takie wyniki odbiegają od spodziewanych. Przy pomiarze kąta rozwarcia pęknięcia (KRP) oraz kąta rozwarcia wierzchołka pęknięcia (KRWP) wykresy globalne otrzymaliśmy dość gładkie i podobne do spodziewanych, zaś lokalne posiadają duże rozrzuty. Różnice między wykresami lokalnymi i globalnymi wynikają ze sposobu określania kąta.

---