POLITECHNIKA ŚWIĘTOKRZYSKA W KIELCACH			LABORATORIUM Z MECHANIKI DOŚWIADCZALNEJ
Dwojewski Grzegorz		Drgania swobodne belki. Pomiar parametrów dynamicznej odporności na pękanie przy pomocy instrumentowanego młota spadowego
WMiBM	ROK AKAD. 2000/2001
GRUPA 32A	ĆWICZENIE 10			OCENA:	PODPIS:

1.Wstęp .

Powszechnie zakłada się że własności mechaniczne metali nie zależą od prędkości odkształcenia. W rzeczywistości jednak własności te są zależne od prędkości odkształcenia, chociaż dla metali w dość szerokim zakresie małych prędkości odkształcenia wpływ ten jest pomijalnie mały. Zakres ten oczywiście umowny i jest on różny dla różnych metali, ale orientacyjnie można powiedzieć, że przy prędkościach odkształcenia rzędu dε/dt<10³ s^-1 ich wpływ na własności np. plastyczne można pominąć. Przy większych prędkościach odkształcenia ich wpływ na zachowanie się metali ma charakter zarówno ilościowy i jakościowy i nie może być pominięty przy formułowaniu związków fizycznych.

Maksymalny zakres prędkości odkształcenia dε/dt, stosowany w badaniach doświadczalnych metali, zawiera się w wielu rzędach dziesiętnych mierzonych w s^-1. Jako statyczną krzywą umocnienia przyjmuje się zazwyczaj krzywą otrzymaną przy prędkościach rzędu 10^-4 s^-1.

Konstrukcje mechaniczne, budowlane są często poddawane obciążeniom z dużymi prędkościami. Bezwładność materiału powoduje, że w obciążanym dynamicznie elemencie generowane są dodatkowe obciążenia, których zmiana jest na ogół rozbieżna w fazie z zewnętrznym wymuszeniem. Propagujące fale sprężyste i drgania próbki powodują złożony stan naprężeń. Odpowiedz materiału w wierzchołku szczeliny na zewnętrzne obciążenia, czyli współczynnik intensywności naprężeń K₁, nie jest już liniową funkcją przemieszczenia punktu przyłożenia siły. Jest to funkcja oscylująca wokół statycznej wartości, przy czym amplituda zmienia się w czasie. Sytuacja taka powoduje, że zachowanie się sprężystej próbki dynamicznie obciążonej zależy od wielu parametrów: masy bijaka, prędkości uderzenia, podatności maszyny.

Pomiar krytycznej , dynamicznej wartości współczynnika intensywności naprężeń K_{1d .}

Pomiar K_1d może mieć miejsce tylko dla materiałów kruchych, dla których naprężenia oblicza się w oparciu o liniową teorię sprężystości Wyznacza się ją na instrumentowanym młocie spadowym. Parametr K_1d wyznacza się na próbkach typu Chapry`ego, które różnią się od klasycznych tym, że na dnie karbu inicjuje się szczelinę zmęczeniową o długości około 1mm. Prędkość uderzenia bijaka nie powinna na ogół przekraczać 505 m/s. Na tak przygotowanym stanowisku przeprowadza się próbę i rejestruje siłę w funkcji czasu. Na ogół otrzymany wykres charakteryzuje się silnymi oscylacjami o zmniejszającej się w czasie amplitudzie. Od wielkości oscylacji zależy sposób analizy otrzymanych krzywych w celu wyznaczenia K_1d. Jeśli zanikają to proponuje się tzw. Analizę prawie statyczną, polegającą na zarejestrowaniu sygnału siły wraz z momentem inicjacji wzrostu pęknięcia.

Moment inicjacji wzrostu pęknięcia oszacować można w różny sposób. Dla materiałów bardzo kruchych moment ten utożsamiany jest z maksymalna siłą występującą tuż przed jej gwałtowną redukcją. Bardziej wiarygodny rezultat otrzymuje się jednak stosując jedną z metod: pomiar momentu spadku naprężeń przed frontem szczeliny oraz pomiar sygnału magnetycznego generowany przez inicjowany wzrost pęknięcia.

Pomiar krytycznej dynamicznej wartości całki J_1d .

Całka J opisywać zachowanie się materiałów sprężysto-plastycznych zawierających szczelinę. Całka J jest niezmiennicza od konturu całkowania. Dla ciął plastycznych całka J jest różnicą pomiędzy energiami potencjalnymi dwóch prawie identycznych, obciążonych elementów różniących się jedynie długością szczeliny da.Ta pozornie błaha w definicji całki J dla ciała nieliniowo sprężystego i plastycznego ma istotne znaczenie. W przypadku obciążenia z dużymi prędkościami, całka J przestaje być całką niezmienniczą od drogi całkowania ze względu na fakt oddziaływania wierzchołka pęknięcia z wielokrotnie odbitą falą sprężystą od powierzchni próbki. Nie traci jednak sensu fizycznego definicja całki J jako różnica energii potencjalnych dwóch obciążonych próbek różniących się jedynie o długość szczeliny da. Prawdziwy zatem jest wzór :

η-parametr określający kształt próbki,

b_o-początkowa długość nie pękniętego odcinka próbki ,

B_N-efektywna grubość próbki. (B=B_N dla próbki gładkiej

Krytyczną wartość całki można by bez problemu obliczyć pod warunkiem , że będzie znane pole A pod krzywą F-s w momencie inicjacji wzrostu szczeliny . Metody wyznaczania wartości całki J można podzielić ze względu na ilość użytych próbek :

• metoda zmian podatności ( metoda jednej próbki ),

• metoda zatrzymanego bijaka ( metoda wielu próbek ).

Wyniki przeprowadzonego doświadczenia.

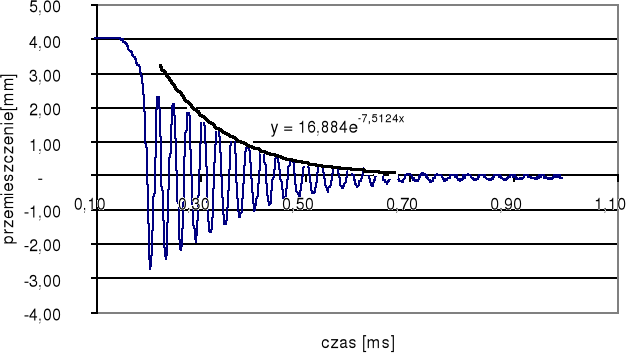
Drgania swobodne tłumione belki

-logarytmiczny dekrement tłumienia
A₁=1mm A₂=0,9688mm
δ=0,0317

T-okres drgań swobodnych

tłumionych.

T=0,03s

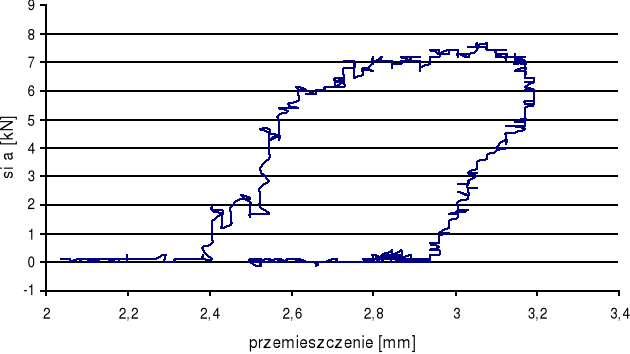
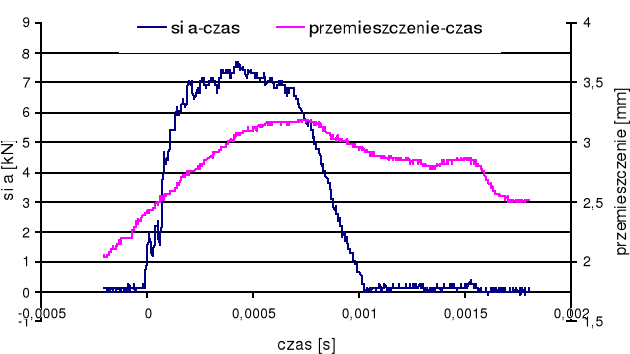
Wyniki wyznaczania dynamicznej odporności na pękanie dla materiałów sprężysto-plastycznych (dynamiczna cłka J) metodą wielu próbek.

	gr	b [mm]	W [mm]	a0 [mm]	da [mm]	A [Nmm]	J[N/mm]	uwagi położenie "StopBloku"	prowadzący
1	32a	10	10	3,780	0,061	5925	190,51	0,5	ZL
2	32b	10	10	3,316	0,612		0,00	0,5	ZL
3	33c	10	10	3,350	1,449	8,77	0,26	1
4	31a	10	10	3,101	1,720		0,00	1
5	31b	10	10	3,194	1,895	10,61	0,31	1,5
6	31c	10	10	3,341	1,968	10,35	0,31	1,5
7		10	10	3,378	2,849	3,04	0,09
8		10	10				0,00
9		10	10	2,608	1,593	4,24	0,11
10	33d	10	10	3,700	2,842	11,48	0,36
11	34c	10	10	3,094	1,968	10,99	0,32	2,5
12	34a	10	10	3,331	1,610	8,10	0,24	1
13	34d	10	10	3,350	0,579	4,67	0,14	0,5
14	34b	10	10	3,107	2,021	11,16	0,32	2,5
	data	16.01.2001			J-średnie	546,22	17,54521
					J-odch.stand

---