Laboratorium z mechaniki ogólnej

ĆWICZENIE NR3

Temat: Ruch płaski.

Cel ćwiczenia: Symulacja ruchu układu materialnego pod wpływem zewnętrznego momentu wymuszającego ruch w programie Matlab przy określonym warunkach początkowych położenia i prędkości. Sporządzenie wykresów zależności położenia i prędkości ciała A od czasu.

1. Wprowadzenie teoretyczne.

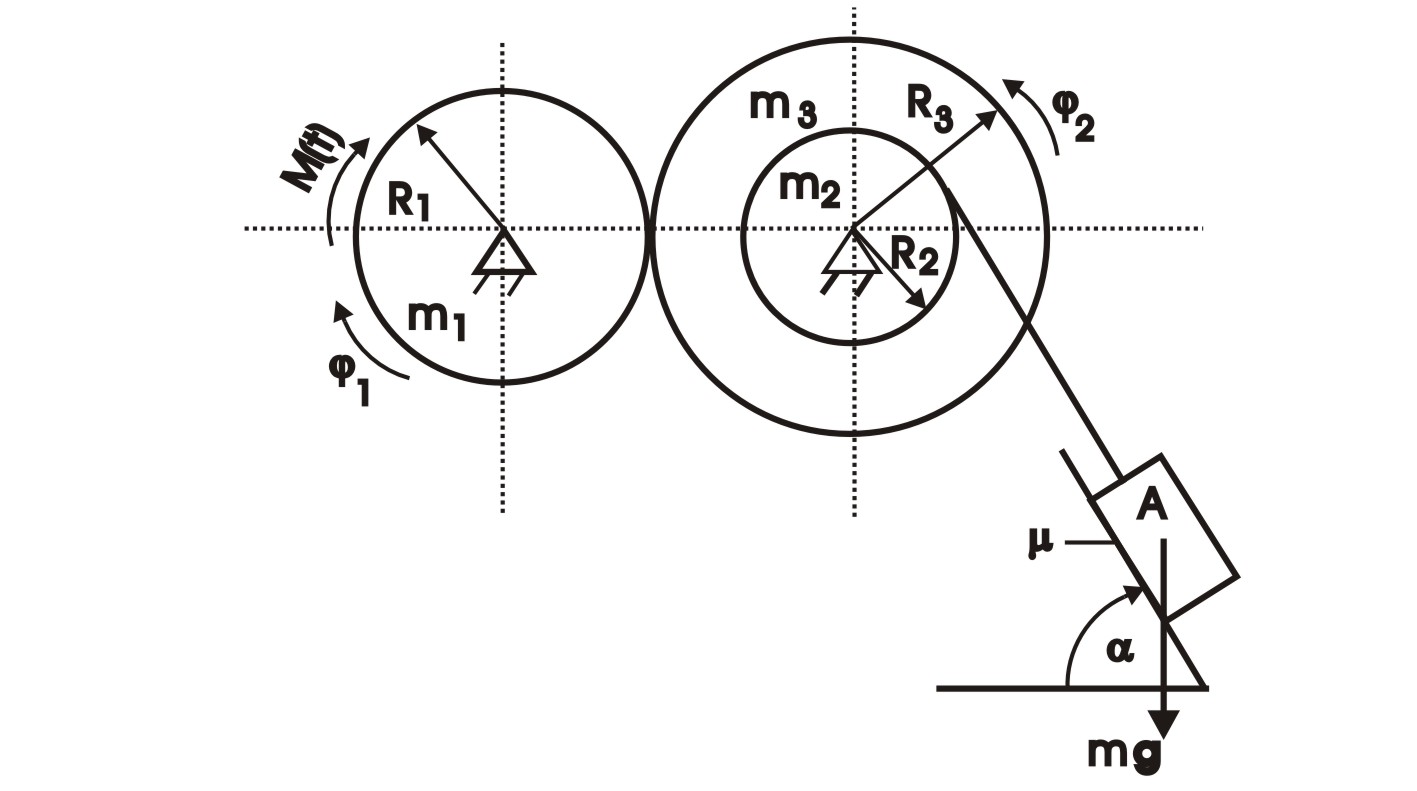
masa ciała A

masa wału pierwszego

masa wału drugiego o promieniu

masa wału drugiego o promieniu

promień wału pierwszego

promień wału pierwszego

promień wału pierwszego

współczynnik tarcia

kąt

przyspieszenie ziemskie

momenty bezwładności dane równaniem (2)

- rozwiązanie, z którego korzystamy w ćwiczeniu

2. Przebieg ćwiczenia

a. Pierwszy sposób

1. Wydaj polecenie simulink

2. Zbuduj następujący schemat:

3. Ustaw warunki początkowe:Integrator2=0
, Integrator1=0

4. Opisz blok Fcn1 następującym wzorem:

((g*m*mi*cos(alfa)*u[1]+g*m*sin(alfa)-((u[2]*R3)/(R1*R2)))/(m+J2/R2^2+(J1*R3^2)/(R1^2*R2^2)))

5. Ustaw parametry symulacji: Simulation/Parameters

Start time:0/Stop time:10/ Min step size/Max step size:0.01

6. Ustaw parametry bloku Step:

Step: Step time:5/ Initial value:0 Final value:300/

7. Załóż plik o nazwie dane.m

m=10;

m1=5;

m2=4;

m3=10;

R1=3;

R2=2.5;

R3=5;

mi=0.1;

alfa=1;

g=9.81;

J1=(m1*R1*R1)/2;

J2=(m2*R2*R2)/2+(m3*R3*R3)/2;

8. Uruchom plik wpisując dane

9. Wydaj polecenie whos

10. Uruchom symulację Simulation/Start

11. Sprawdź, jaki powstały wykresy (kliknij na Scope).

b. Drugi sposób

1. Założ pliki tekstowe o nazwie row2t.m

function [dy]=row2t(t,y)

global kroki m m1 m2 m3 R1 R2 R3 mi alfa g J1 J2

if (t>5)

M=300;

else

M=0;

end

kroki=kroki+1;

dy=zeros(2,1);

dy(1)=y(2); %y(1) to jest x,y(2) to jest x',dy(2) to jest x''

dy(2)=-((g*m*mi*cos(alfa)*sign(y(2))+g*m*sin(alfa)-((M*R3)/(R1*R2)))/(m+J2/R2^2+(J1*R3^2)/(R1^2*R2^2)));

2. Drugi plik o nazwie licztot.m

global kroki m m1 m2 m3 R1 R2 R3 mi alfa g J1 J2

m=10;

m1=5;

m2=4;

m3=10;

R1=3;

R2=2.5;

R3=5;

mi=0.1;

alfa=1;

g=9.81;

J1=(m1*R1*R1)/2;

J2=(m2*R2*R2)/2+(m3*R3*R3)/2;

t0=0;t2=20; %przedział czasowy symulacji

x0=[0 0]; %x,v - warunki początkowe

kroki=0;

options = odeset('RelTol',1e-5,'AbsTol',[1e-4 1e-4 1e-5]);

[t,x]=ode45('row2t',t0,t2,x0,options ); %wywołujemy funkcję całkującą z parametrami funkcji row

disp('obliczenia wykonano dla następującej ilości kroków')

kroki

plot(t,x(:,1),t,x(:,2)),title('x,v');

3. Uruchom symulację wpisując słowo licztot

3. Zadania do samodzielnego wykonania

1. Wyprowadź równanie ruchu

2. Zmień moment M tak aby działał od 5 s do 12 s o wartości 300

3. Wyznacz moment bezwładności dla wału II.

4. Oblicz wartość M, dla której układ pozostaje w równowadze. Podaj wzór, w/g którego ta wartość została obliczona.

5. Przeprowadź symulację dla obliczonej wartości M. Moment M jest stały w czasie całej symulacji od 0 do 20 s.