Politechnika Śląska Katowice, dnia 16.03.10r.

Wydział Transportu

ĆWICZENIA LABOLATORYJNE Z FIZYKI

Sprawozdanie z ćwiczenia nr 10

Temat ćwiczenia: Pomiar czasu zderzeń kul i wyznaczanie parametrów deformacji.

Grupa T16

Sekcja nr X

……………….

……………….

Przebieg ćwiczenia.

1. Złożyć układ pomiarowy według schematu . Kulki zawieszone są na cienkich przewodach umocowanych do obudowy. Układ posiada dwa elektromagnesy służące do utrzymywania kul w położeniu odchylonym od pionu o kąt
   .

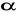
2. Zmierzyć odległości kul od podstawy, gdy kule zwisają swobodnie. Zanotować pojemność kondensatora C i średnicę kul d=3,18cm.

3. Włączyć zasilacz i ustawić napięcie 30V. Odchylić kulki tak, aby dotknęły elektromagnesów i zmierzyć ich odległość od podstawy.

4. Naładować kondensator poprzez włączenie na kilka sekund wyłącznika W
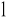
   i zanotować napięcie U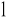
   , jakie wskazuje woltomierz.

5. Naciskając na chwilę wyłącznik W
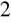
   zwolnić kule. Po zderzeniu powinny one zostać przyciągnięte przez elektromagnesy. Zanotować napięcie U w chwilę po zetknięciu..

6. Pomiary opisane w punkcie 4 i 5 powtórzyć dla 10 wartości od 1
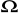
   do 10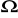
   , zmieniając opór co jeden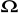
   .

Opracowanie wyników pomiarów.

Obliczenie wartości średnich oraz ich niepewności.

a) odległości kul od podstawy, gdy kule zwisają swobodnie:

Wyznaczona odległość wynosi:

L₁ = (1,070 ± 0,008) · 10^-1 [m]

b) odległości kul od podstawy, gdy kule dotykają elektromagnesów:

Wyznaczona odległość wynosi:

L₂ = (1,170 ± 0,008) · 10^-1 [m]

c) napięcia U (średnia 5 pomiarów; odczytane w chwilę po zderzeniu)

R [Ω]	Uśr [V]
1	0,22
2	0,42
3	1,46
4	2,90
5	4,30
6	6,14
7	7,30
8	9,04
9	10,16
10	11,62

Sporządzenie wykresu zależności 1/ln(U_o/U) = f(R).

Wykres 1

R [Ω]	Uśr [V]	1/ln(Uo/U) [1]
1	0,22	0,203
2	0,42	0,234
3	1,46	0,330
4	2,90	0,428
5	4,30	0,514
6	6,14	0,630
7	7,30	0,707
8	9,04	0,834
9	10,16	0,924
10	11,62	1,054

Obliczenie współczynników kierunkowych prostej aproksymującej wyniki przedstawione na wykresie 1/ln(U_o/U) = f(R).

Wyznaczone współczynniki prostej 1/ln(U_o/U) = aR + b :

a = (0,09 ± 0,02) [1/]

b = (0,05 ± 0,13) [1]

Obliczenie czasu rozładowania kondensatora.

W obliczeniach wykorzystujemy następujący wzór:

Porównując powyższy wzór z równaniem prostej aproksymującej:

1/ln(U_o/U) = aR + b

otrzymujemy wzór na czas rozładowania kondensatora:

=
[s]

gdzie:

C = 10^{- 5} [F] - pojemność kondensatora

a = (0,09 ± 0,02) [1/] - współczynnik kierunkowy prostej aproksymującej

Obliczenie niepewności t czasu rozładowania kondensatora.

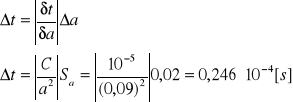
Czas rozładowania kondensatora t wynosi:

t = (1,111 ± 0,246) · 10^-4 [s]

Obliczenie wielkości h ugięcia czaszy kuli podczas zderzenia.

Obliczenia wykonujemy wg. wzoru:

=

gdzie:

t = (1,111 ± 0,246) · 10^-4 [s] - czas rozładowania kondensatora

g = 9,81 [m/s²] - przyspieszenie grawitacyjne

H = H₂ - H₁ - różnica wysokości kul

Niepewność wyznaczenia różnicy wysokości kul wynosi:

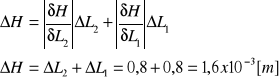
H = (0,100 ± 0,016) · 10^-1 [m].

Niepewność ugięcia h czaszy kuli podczas zderzenia.

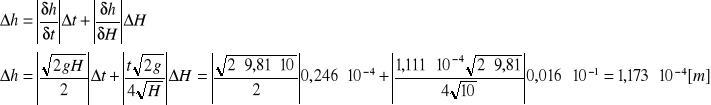
Wyznaczona wartość h ugięcia czaszy wynosi:

h = (7,781 ± 1,173) · 10^-4 [m]

6. Obliczenie modułu sprężystości kuli.

Wzór do wyznaczania E jest następujący:

=

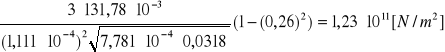
gdzie:

m = 131,78 · 10^{- 3} [kg] - masa kuli

 = 0,26 - współczynnik Poissona dla żelaza lanego

d = 0,318 · 10^-1 [m] - średnica kul

t = (1,111 ± 0,246) · 10^-4 [s] - czas rozładowania kondensatora (czas zderzenia kul)

h = (7,781 ± 1,173) · 10^-4 [m] - ugięcie czaszy kuli

Niepewność wyznaczenia E modułu sprężystości kuli.

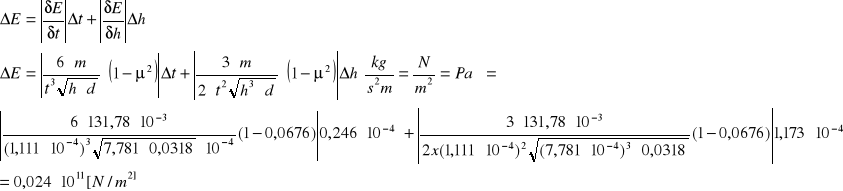
Moduł sprężystości kuli wynosi:

E = (1,23 ± 0,024) · 10¹¹ [N/m²]

7. Porównanie wyznaczonego modułu sprężystości E z wartością E_t.

=

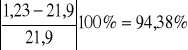
E = (1,23 ± 0,024) · 10¹¹ [N/m²] - moduł sprężystości wyznaczony doświadczalnie

E_t = 21,9 · 10¹⁰ [N/m²] - wartość odczytana z tablic (dla stali)

W obliczeniach uzyskaliśmy błąd względny procentowy  = 94,38%.

ZESTAWIENIE WYNIKÓW POMIARÓW

• t = (1,111 ± 0,246) · 10^-4 [s] - czas rozładowania kondensatora (czas zderzenia kul)

• h = (7,781 ± 1,173) · 10^-4 [m] - ugięcie czaszy kuli

• E = (1,23 ± 0,024) · 10¹¹ [N/m²] - moduł sprężystości kuli

•  = 94,38% - błąd względny uzyskany z porównania obliczonego modułu sprężystości z danymi tablicowymi.

WNIOSKI

1. Na podstawie wykresu zależności 1/ln(U_o/U) = f(R) stwierdzamy, że jest to zależność liniowa. Zależność tą aproksymowaliśmy prostą o równaniu 1/ln(U_o/U) = aR + b gdzie:

a = (0,09 ± 0,02) [1/]

b = (0,05 ± 0,13) [1]

Obliczona funkcja posłużyła następnie do wyznaczenia czasu t rozładowania kondensatora.

2. Błąd względny obliczonej wartości E modułu Younga jest spowodowany niepewnościami wyznaczenia wielkości, które zostały użyte do policzenia E. Tak duża wartość błędu może wynikać z nakładania się kolejnych niepewności.

3. Obliczenia, na podstawie których wyznaczyliśmy moduł sprężystości kuli opierają się na prawie Hooke'a, mówiącego o tym, że odkształcenie materiału jest proporcjonalne do siły działającej na ciało dla przedziału od zera do punktu będącego granicą sprężystości. Po przekroczeniu granicy sprężystości odkształcenie przestaje być liniową funkcją naprężenia.

---