Ćwiczenie nr 22 Aleksandra Drzewiecka

Małgorzata Giszczak

PRAWO PODZIAŁU NERNSTA

1.Układy trójskładnikowe-jednofazowe:

W stałej temperaturze, równowaga pomiędzy fazami skondensowanymi będzie równowagą dwuzmienną, ponieważ temperatura i stężenie substancji rozpuszczonej w fazie ciekłej wyznacza jednocześnie, stężenie tej substancji w fazie drugiej, i to niezależnie od stanu skupienia substancji rozpuszczonej, jednak substancja rozpuszczona nie może powiększać wzajemnej rozpuszczalności obu cieczy. Jeśli substancją rozpuszczoną jest gaz -to jego stężenia c₁ i c₂ są proporcjonalne do ciśnienia p zgodnie z prawem Henry`ego.

2.Prawo podziału Nernsta:

Prawo głoszące, że dla dwu nie mieszających się, będących w kontakcie i pozostających ze sobą w równowadze cieczy, stosunek stężeń (ściślej aktywności) trzeciego składnika, rozpuszczonego w każdej z tych cieczy, jest stały w danych warunkach temperatury i ciśnienia. Stosunek ów nazywa się współczynnikiem podziału. Zgodnie z powyższym , mamy :

K=
gdzie: K- stała podziału

i
- aktywności w poszczególnych warstwach

Prawo to w postaci prostej jest słuszne tylko tych przypadkach, gdy po doprowadzeniu do stanu równowagi, substancja rozpuszczona nie zmienia swojego stanu cząsteczkowego tj: gdy w obu rozpuszczalnikach nie dysocjuje ani też nie asocjuje, a temperatura pozostaje stała.

Wzór Nernsta: K -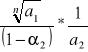

A w rozcieńczonych aktywności możemy zastąpić stężeniami : K -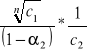

3. Wykonanie ćwiczenia:

W kolbie miarowej na 50 cm³ sporządzamy roztwór zawierający 2,5 grama kwasu benzoesowego w toluenie. Trzy roztwory robocze otrzymujemy pobierając pipetą miarową odpowiednio 3,8 cm³, 7,5 cm³ , 15 cm³ roztworu podstawowego i dopełniamy do 25 cm³ toluenem do kreski. Następnie przelewamy je do rozdzielaczy, w którym znajduje się 50 cm³ wody i mieszamy dzięki wytrząsarce ręcznej. Następnie gdy warstwa wodna będzie klarowna i wypuszczamy warstwę wodną do zlewki. Następnie odpipetowujemy dwie próbki po 10 cm³ i miareczkujemy rozpuszczony w nich kwas 0.01 M roztworem NaOH wobec fenoloftaleiny.

4. Opracowanie wyników (wyznaczanie stałych K i n ):

Ilość moli kwasu benzoesowego w rozdzielaczu	Średnia ilość cm^3 NaOH	c2 [mol/dm^3]	c1 [mol/dm^3]	log[c2(1-α2)]	log[c1]
1,55 * 10^-3	10,03	0,01003	0,0419	- 2.03	-1,37
3,06 * 10^-3	11,05	0,01105	0,1003	- 1,99	-0,99
6,12* 10^-3	18,39	0,01839	0,2080	- 1,76	-0,68
8,16* 10^-3	21,18	0,02118	0,2840	- 1,69	-0,54

M_{mol kw.benz}. = 122,123g

1 mol - 122,123 g

x - 2,5 g

x=0,0204 mola kwasu benzoesowego

0,0204 mola - 50 cm³

x - 1000 cm³

x - 0,408 stężenie kwasu benzoesowego

Dla pierwszego rozdzielacza:

c₂ =
= 0,01003

0,408 - 1000 cm³

x - 3,8 cm³

x = 1,55 * 10^-3

c₁=
=
= 0,0419

K=
=
= 4,17

Dla drugiego rozdzielacza:

c₂ =
= 0,01105

0,408 - 1000 cm³

x - 7,5 cm³

x = 3,06 * 10^-3

c₁=
=
= 0,1003

K=
=
= 9,077

Dla trzeciego rozdzielacza:

c₂ =
= 0,01839

0,408 - 1000 cm³

x - 15 cm³

x = 6,12* 10^-3

c₁=
=
= 0,208

K=
=
= 11,31

Dla czwartego rozdzielacza:

c₂ =
= 0,02118

0,408 - 1000 cm³

x - 20 cm³

x = 8,16* 10^-3

c₁=
=
= 0,2840

K=
=
= 13,408

1. α₂=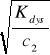
czyli α₂=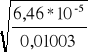
= 0,080

2. α₂=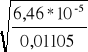
= 0,076

3. α₂=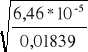
= 0,059

4. α₂=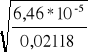
= 0,055

dla I-wszego rozdzielacza : log[c₂(1-α₂)] = log[0,01003*(1-0,080)] = - 2.03

dla II-ego rozdzielacza : log[c₂(1-α₂)] = log[0,01105*(1-0,076)] = - 1,99 dla III-ego rozdzielacza : log[c₂(1-α₂)] = log[0,01839*(1-0,059)] = - 1,76 dla IV-ego rozdzielacza : log[c₂(1-α₂)] = log[0,02118*(1-0,055)] = - 1,69

dla I-wszego rozdzielacza: log[c₁] = log[0,0419] = -1,37

dla II-ego rozdzielacza: log[c₁] = log[0,1003] = -0,99

dla III-ego rozdzielacza: log[c₁] = log[0,2080] = -0,68

dla IV-ego rozdzielacza: log[c₁] = log[0,2840] = -0,54

K_dys = 6,46 *10^-5

Obliczenie K:

Równanie funkcji: y-y₁=
(x - x₁)

A(-1,37;-2,03)

B(-0,54;-1,69)

y + 2,03 =
(x +1,37)

y = 0,4096*x - 1,4687

Przecięcie z osią OY w punkcie -1,47 (y =0,4096*0-1,4687 )

log[K] = -1,47

K = 10^-1,47 = 0,00338

Obliczenie n:

Δy = - 0,54 - (-1,34) = 0,83

Δx = -1,69 -(- 2,03) = 0,34

)=
=
= 0,4096

n =
=1 / 0,4096 = 2,44

---