Robert Maniura

Sprawozdanie z ćwiczenia nr 21: Wyznaczanie masy cząsteczkowej metodą ebuliometryczną.

1. Wstęp teoretyczny:

Pośród rozlicznych właściwości roztworów istnieje jedna ich grupa, której wspólną cechą jest ich zależność od liczby cząsteczek (moli) substancji rozpuszczonej. Do tych, koligatywnych, właściwości roztworów zaliczamy: obniżenie temperatury krzep­nięcia roztworu w stosunku do czystego rozpuszczal­nika, podwyższenie temperatury wrzenia roztworu w stosunku do czystego rozpuszczalnika oraz ciśnie­nie osmotyczne roztworów. Właściwości te wynikają z faktu, że w procesie tworzenia roztworu obniża się jego entalpia swobodna.

Rozważmy przykładowo zjawisko zmiany tempera­tury krzepnięcia substancji przez dodatek substancji rozpuszczonej. Metoda fizykochemiczna oparta na tym zjawisku nosi nazwę kriometrii.

Niech roztwór dwuskładnikowy o składzie (x₁, x₂) w stanie ciekłym ma temperaturę początkową T_p, gdzie x₁ oznacza ułamek molowy roz­puszczalnika. Przy obniżaniu temperatury, w tem­peraturze T_k rozpocznie się wydzielanie z roztworu czystego rozpuszczalnika. Zgodnie z regułą faz Gibbsa, liczba stopni swobody (n) w tym dwu­składnikowym ( = 2) i dwufazowym ( = 2) ukła­dzie wynosi 2:

n =  -  + 2 = 2

Jednym z nich jest ciśnienie, drugim zaś temperatura lub skład. Ponieważ ciśnienie jest ustalone (p = const) zatem jedynym stopniem swobody jest temperatura lub skład. Te dwa parametry nie mogą więc być niezależne - musi istnieć równanie poda­jące zależność temperatury krzepnięcia od składu roztworu. Znajdźmy to równanie.

Potencjał chemiczny wydzielającego się w tempera­turze T_k czystego rozpuszczalnika jest równy standardowemu potencjałowi chemicznemu w tej tem­peraturze:

Potencjał chemiczny rozpuszczalnika w roztworze (faza ciekła) zależy od jego aktywności a₁:

W stanie równowagi te potencjały chemiczne są sobie równe:

lub

Różnica (
) jest równa zmianie entalpii swobodnej krystalizacji jednego mola czystego rozpuszczalnika G_k w temperaturze T_k:

Zgodnie z II zasadą termodynamiki:

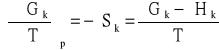
(1)

zaś różniczkując powyższe równanie obustronnie wzglę­dem temperatury mamy:

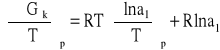
(2)

Przyrównanie prawych stron równań (1)i (2) prowadzi do zależności:

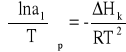
(3)

w której H_k oznacza zmianę entalpii w procesie krystalizacji 1 mola rozpuszczalnika.

Całkowanie równania (3) uzależnione jest od zakresu temperatur. Dla temperatur T_k niezbyt odle­głych od temperatury krystalizacji czystego rozpusz­czalnika T_o, można przyjąć entalpię krystalizacji H_k za wielkość stałą, niezależną od temperatury. Przy takim założeniu całkowanie równania (3) począwszy od temperatury krystalizacji czystego rozpuszczalnika T_o (w której a₁ = 1) do temperatury krystalizacji roztworu T_k (w której aktywność roz­puszczalnika w roztworze wynosi a₁) prowadzi kolejno:

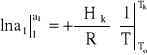
(4)

do równania:

(5)

Jeżeli roztwór jest ponadto dostatecznie rozcieńczony, to aktywność rozpuszczalnika można zastąpić przez jego ułamek molowy x_1, a ponieważ:

x₁ = 1 - x₂

zatem dla małych wartości x₂:

-lnx₁ = -ln(1 - x₂) = x₂

gdzie x₂ jest ułamkiem molowym substancji rozpuszczonej:

(6)

W równaniu tym m₁ i m₂ oznaczają masy rozpusz­czalnika i substancji rozpuszczonej, zaś M₁ i M₂ odpowiednie masy cząsteczkowe. Zatem równanie (5) przyjmie postać:

(7)

Wyrażając stężenie roztworu w skali molarności m [mol/l000 g] rozpuszczalnika mamy:

(8)

a stąd i z równania (6):

(9)

Oznaczając obniżenie temperatury krzepnięcia roz­tworu w stosunku do temperatury krzepnięcia czystego rozpuszczalnika przez T_k:

T_k = T_o - T_k

oraz przyjmując, że:

otrzymujemy z równań (7) i (9):

T_k = K_km (10)

gdzie stała K_k zwana stałą kriometryczną zawiera wszystkie wielkości stałe:

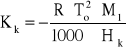
(11)

Znak „-„ w równaniu na stalą krioskopową po­chodzi stąd, że w rozważaniach posłużono się entalpią krystalizacji, a nie jak zwykle ciepłem top­nienia (H_k < 0).

(12)

Stała kriometryczna jest równa obniżeniu tempe­ratury krzepnięcia roztworu zawierającego w 1000 g rozpuszczalnika 1 mol substancji rozpuszczonej. Jest to wielkość charakterystyczna dla rozpuszczal­nika.

Przyjęte założenia ograniczają stosowalność rów­nania (10) jedynie do roztworów rozcieńczonych. Przy roztworach bardziej stężonych założenia te należy odrzucić.

Zgodnie z prawem Kirchhoffa entalpię krystalizacji rozpuszczalnika w temperaturze krzepnięcia roz­tworu T_k należy przedstawić za pomocą równania:

H_k = H_o + C_p(T­_k - T_o) = H_o - C_p*T­_k (13)

w którym H_o oznacza entalpię krystalizacji roz­puszczalnika w temperaturze krystalizacji czystego rozpuszczalnika T_o, zaś C_p jest różnicą ciepeł molo­wych stałego i ciekłego rozpuszczalnika. Wprowadzając równanie (13) dorównania (5) oraz rezygnując z przybliżenia
otrzymuje się:

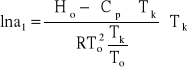
(14)

Utrzymując założenie o idealnym zachowaniu roz­puszczalnika można równanie (14) doprowadzić do postaci:

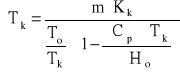
(15)

w której mianownik określa poprawkę w stosunku do równania (10). Jeżeli T_k jest rzędu 2 - 3°, to błąd wynikający z nieuwzględnienia wyrażenia w mianowniku nie przekracza 1 - 2 %.

Podstawowe równanie kriometrii (10) speł­nione jest jedynie przez idealne roztwory nieelektro­litów. W rozcieńczonych roztworach mocnych elek­trolitów w miejsce molarności we wzorze (10) należy stosować iloczyn l*m, gdzie l jest liczbą jo­nów tworzących się w wyniku dysocjacji cząsteczki elektrolitu. W rozcieńczonych roztworach słabych elektrolitów należy uwzględnić dysocjację; w miejsce stężenia molarnego -dla słabego elektrolitu binar­nego - należy wstawić wartość m(1 + ), gdzie  jest stopniem dysocjacji.

W bardziej stężonych roztworach elektrolitów na­leży uwzględnić współczynniki aktywności.

Termodynamiczną konsekwencją procesu tworze­nia roztworu (dodania substancji rozpuszczonej do rozpuszczalnika) jest spadek entalpii swobodnej roztworu. Spadek entalpii swobodnej prowadzi w przypadku roztworów doskonałych i większości roztworów rzeczywistych do obniżenia prężności par rozpuszczalnika nad roztworem w stosunku do prężności par nad czystym rozpuszczalnikiem. Kon­sekwencją tego zjawiska jest obniżanie tempera­tury krzepnięcia roztworu w stosunku do tempera­tury krzepnięcia czystego rozpuszczalnika, a także podwyższanie temperatury wrzenia roztworu w sto­sunku do temperatury wrzenia czystego rozpuszczalnika. Na zjawisku podwyższania temperatury wrzenia roztworu oparta jest fizykoche­miczna metoda badawcza zwana ebuliometrią.

Podobnie jak w kriometrii, wielkość podwyższenia temperatury wrzenia w ebuliometrii (T_w) związana jest ze stężeniem roztworu (m). Rozważanie analo­giczne, jak przy wyprowadzeniu równania (10) prowadzi do równania:

T_w = K_Em (16)

Stała ebuliometryczna K_E występująca w tym rów­naniu określona jest równaniem analogicznym do (11):

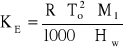
(17)

w którym T_o jest odpowiednio temperaturą wrzenia czystego rozpuszczalnika, zaś H_w molowym ciep­łem parowania. Stała ebuliometryczna podająca podwyższenie temperatury wrzenia obserwowane dla roztworu 1 molarnego, jest - podobnie jak stała kriometryczna­ wielkością charakterystyczną dla rozpuszczalnika i niezależną od rodzaju substancji rozpuszczonej.

Zastrzeżenia czynione przy wyprowadzaniu równa­nia (10) słuszne są także dla podstawowego równania ebuliometrii (17).

2. Opracowanie wyników:

Masy próbek obliczam z następującej zależności:

gdzie: m_s - masa substancji; m_pk - masa kolby z naważką substancji; m_k - masa pustej kolby.

• naważka I: m_s = 54,3815 - 51,3645 = 3,017 g

• naważka II: m_s = 53,3608 - 51,8085 = 1,5523 g

• naważka III: m_s = 49,2515 - 47,1826 = 2,0689 g

• naważka IV: m_s = 48,9855 - 46,8677 = 2,1178 g

Równanie termistora jest następujące:

z równania termistora można obliczyć temperaturę wrzenia rozpuszczalnika i roztworów (
= -9,2872 ± 0,0571; b = -3573,2239 ± 21,2883):

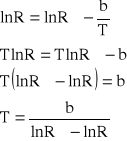
Temperatura wrzenia (R = 1,371 k) dla czystego rozpuszczalnika (H₂O) wynosi: T_wrz.(w) = 372,10 K.

Temperatura wrzenia (R = 1,361 k) dla roztworu z naważką I wynosi: T_wrz.(1) = 372,39 K.

Temperatura wrzenia (R = 1,355 k) dla roztworu z naważką I, II i III wynosi: T_wrz.(2) = 372,56 K.

Temperatura wrzenia (R = 1,352 k) dla roztworu z naważką I, II, III i IV wynosi: T_wrz.(3) = 372,65 K.

Molarność badanych roztworów i masa molowa substancji:

Molarność roztworów obliczyć można z następującej zależności:

gdzie: T_w - przyrost temperatury wrzenia (T_w = T_wrz.(x) - T_wrz.(w); x - oznacza odpowiedni pomiar: 1, 2, 3); K_E - stała ebuliometryczna wody (K_E = 0,521 [K*kg/mol]); m - molarność roztworu.

Masa molowa substancji:

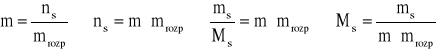
gdzie: m - molarność roztworu; n_s - liczba moli substancji; m_rozp - masa rozpuszczalnika [kg]; m_s - masa substancji w roztworze [g]; M_s - masa molowa substancji.

Pomiar	Masa substancji w roztworze ms [g]	Przyrost temperatury Tw [K]	Molarność roztworu [mol/kg]	Masa molowa [g/mol]
1	naważka I ms = 3,017	0,29	0,5566	54,20
2	naważka I + II + III ms = 6,6382	0,46	0,8829	75,19
3	naważka I + II + III + IV ms = 8,756	0,55	1,0557	82,94

Średnia masa molowa substancji wynosi 70,78 [g/mol]

W przypadku małej liczby pomiarów średnia może różnić się dość znacznie od wartości prawdziwej. Dlatego wygodniej jest wtedy określić przedział, w którym wartość rzeczywista znajduje się z dużym prawdopodobieństwem. Taki przedział nazywamy przedziałem ufności. Wyznaczam przedział ufności dla prawdopodobieństwa 95% (p = 0,95 ; α = 0,05)

μ = X ⁺ t * s

gdzie: X - średnia arytmetyczna; t - wartość funkcji Studenta, wartość współczynnika „t” dla prawdopodobieństwa 95% (dla 3 pomiarów), t = 4,303 dla K = n - 1 = 2

s - odchylenie standardowe średniej arytmetycznej, obliczane ze wzoru:

s =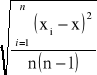

gdzie: x_i - kolejne wyniki; x - średnia arytmetyczna wyników; n - ilość wyników (n=5).

s = 8,39

Masa molowa substancji wynosi 70,78 ± 36,1 [g/mol]

Porównanie z wartością tablicową: masa molowa tiomocznika wynosi 76,1226 [g/mol] zaś wartość eksperymentalna wynosi 70,78 [g/mol] a błąd procentowy wynosi 7,02 %.

3. Wnioski:

Cel ćwiczenia (wyznaczenie masy molowej substancji) został osiągnięty. Wartość pojemności jonitu wyznaczona przeze jest obarczona błędem 7,02 %. Przedział ufności jest bardzo duży ponieważ wartości masy molowej są bardzo rozbieżne. Rozbieżność wartości może być spowodowane niedokładnościami w czasie pomiarów.

5

---