Nr. Ćwiczenia: 0 |
Temat: Wyznaczanie niepewności pomiaru.
|
||
Kierunek: Mechatronika |
Imię i Nazwisko:
|
||
Data wykonania: 2.10.2012r. |
Rok: I rok |
Grupa: 2 |
Zaliczenie:
|
1.WSTĘP.
W wyznaczaniu niepewności pomiaru rozróżniamy 3 rodzaje błędów pomiarowych.
Pierwszym z nich są Błędy systematyczne , wynikają one najczęściej z wadliwego funkcjonowania przyrządów pomiarowych. Błędy systematyczne można zmniejszać nieograniczenie przez doskonalenie metody pomiarowej.
Następnym rodzajem są Błędy grube , powstają one najczęściej w skutek omyłkowego odczytu na skali przyrządu. Błędy te można stosunkowo zauważyć.
Kolejnym rodzajem są Błędy przypadkowe , są one związane z samą istotą pomiaru i nie można ich uniknąć. Źródłami są :
Niedoskonałości zmysłów (refleks);
Oddziaływanie otoczenia ( temperatura , ciśnienie);
Niedokładność przyrządów.
itp.
Zawsze powinniśmy podawać wynik w postaci:
x ± ∆x
Błędy przypadkowe bezpośrednich pomiarów są jednakowo dokładne , jeżeli wielokrotnie będziemy powtarzać pomiar wielkości, to stwierdzimy, że wyniki pomiarów :
X1 , X2 , … , Xn
różnią się między sobą. Muszą się naturalnie różnić na ogół od wartości której nie znamy, a musimy zmierzyć.
Niepewnością i -tego pomiaru będziemy nazywać.
∆x p1 ≡ x1; - xp
z teorii błędów opracowanych przez Gaussa wynika że wartość najbardziej zbliżone do wartości prawdziwej jest średnia arytmetyczna.
x1 + x2+ … +xn = ![]()
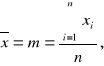
Różnicę
∆xi = x1 -![]()
nazywamy błędem pozornym pomiaru.
Gauss opracowując teorię błędów założył, że chodzi wyłącznie o błędy przypadkowe oraz, że ich rozkład jest normalny tzn.
błędy małe występują w pomiarze częściej niż duże.
błędy o znakach ujemnych są równie częste jak błędy o znakach dodatnich.
Teoretyczny rozkład wyników pomiarów przedstawia tzw. „krzywa dzwonowa” zwana krzywą błędów Gaussa (1794 r.)
Dla dużej liczby pomiarów krzywa ta jest symetryczna.
Krzywa Gaussa jest krzywą uniwersalną w przyrodzie, taki rozkład można otrzymać analizując:
wzrost itd. mężczyzn
czas życia muszek
prędkość cząsteczek gazu itd.
Przeprowadzając serię pomiarów o tym samym stopniu dokładności jako niepewność pomiaru można przyjąć tzw. Średni błąd kwadratowy średniej wartości pomiarów.
Przez średni błąd kwadratowy rozumiemy takie odchylenie pomiaru od wartości średniej
, że w zakreskowanym polu rozkładu Gaussa leży 68,3 % wszystkich pomiarów.
Wartość
średniego błędu kwadratowego jest równa
Wynik pomiaru zapisujemy wtedy następująco
Chcąc skorzystać z tej metody obliczania niepewności pomiaru musimy wykonać serię co najmniej pięciu pomiarów.
b) Obliczanie błędu maksymalnego
Rozważmy przypadek, kiedy pomiar jest stosunkowo mało dokładny i powtarzanie pomiarów daje ten sam wynik lub pomiarów jest mało 2-3. W takim przypadku szacowanie błędu dokonuje się na podstawie klasy przyrządu, a jeżeli klasa nie jest znana to zakładamy, że prawidłowy odczyt jest możliwy co najwyżej z błędem
równym połowie najmniejszej działki, w jaką zaopatrzono skalę przyrządu.
Ogólnie jeżeli
wtedy różniczka
a zastępując nieskończenie małe przez błędy
otrzymamy
2.PRZEBIEG ĆWICZENIA:
W opisywanym doświadczeniu mierzymy dokładnie dziesięciokrotnie długość sali laboratoryjnej. Następnie porównujemy wyniki z dokładnością co do milimetra , próbując uniknąć błędów pomiarowych. Do pomiarów wykorzystujemy taśmę mierniczą.
Następnie wyliczamy średnią długości sali.
oraz odchylenia standardowego:
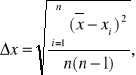
3.TABELA POMIARÓW:
481,5 + 206,5 = 687 |
481,6 + 205,5 = 687,1 |
481,4 + 205,5 = 686,9 |
|
481,7 + 205,2 = 686,9 |
421 + 265,9 = 686,9 |
421,1 + 265,9 = 687 |
|
390,8 + 296 = 686,8 |
390,8 + 296,1 = 686,9 |
265,7 + 421 = 686,7 |
|
265,7 + 421,1 = 686,8 |
|||
4. Obliczenia:
Średnia : 687 + 687,1 + 686,9 + 686,9 + 686,9 + 687 + 686,8 + 686,9 + 686,7 + 686,8 = 686,9 |
(0,1)2 = 0,01
(0,2)2 = 0,04
(0)2 = 0
(0)2 = 0
(0)2 = 0
(0,1)2 = 0,01
(0,1)2 = 0,01
(0)2 = 0
(0,2)2 = 0,04
(0,1)2 = 0,01
∑ = 0,12
Odchylenie standardowe:
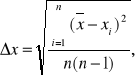
∆x![]()
= ![]()
= 0,0365143 ≈ 0,04
∆x =(686,90 ± 0,04) cm.
1
Wyszukiwarka
Podobne podstrony:
OPis 88, dc, GPF, Fizyka lab, Ćw.88.90
Opis 7, dc, GPF, Fizyka lab, Ćw.7
Sprawozdanie6, dc, GPF, Fizyka lab, Ćw. 11
77, dc, GPF, Fizyka lab, Ćw.88.90
teoria przezwojowana, Semestr 3 moje, FIZYKA LAB, fizyka cw 1
Cw.47-Charakterystyka fotoogniwa1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, s
Opis 1(1), dc, GPF, Fizyka lab, Ćw. 6
Ćw.8, dc, GPF, Fizyka lab, Ściągi
Opis 52, dc, GPF, Fizyka lab, Ćw. 52,57
ćw 6 całe adzio, dc, GPF, Fizyka lab, cw6, 1
sprawko 66 stała Plancka, ATH - ZiIP, Inne semestry, Fizyka - ćw, sprawka - lab
sprawko 61 sonda płomykowa, ATH - ZiIP, Inne semestry, Fizyka - ćw, sprawka - lab
Sprawozdanie7, dc, GPF, Fizyka lab, Ćw.88.90
więcej podobnych podstron