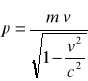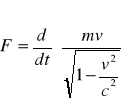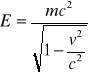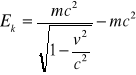1.1 Liczba stopni swobody : Płaszczyzna S=2N-K; Przestrzeń S=3N-K
N - liczna punktów charakterystycznych, K - liczba więzów. S1+S2-W (liczba stopni swobody 2 ciał połączonych W więzami)
1.2 Więzy - w mechanice, każdy rodzaj ograniczenia ruchu nałożonego na poruszające się ciało. Najczęściej dzieli się je ze względu na sposób ich określenia: więzy holonomiczne - takie, które można opisać prostymi równaniami różniczkowymi, więzy nieholonomiczne - takie, których nie da się opisać pojedynczymi równaniami różniczkowymi. Ograniczenia ruchu bardzo często zależą też od czasu. W takim kontekście rozróżnia się: więzy skleronomiczne - nie zależą one jawnie od czasu, więzy reonomiczne - zależą jawnie od czasu.
Liczba całek ruchu ciała o f stopniach swobody
Własności całek ruchu związanych z czasem i przestrzenią
1.5 Zasady zachowania są to prawa fizyczne stwierdzające, że w układzie odosobnionym wartości liczbowe niektórych wielkości fizycznych nie ulegają czasowym zmianom, niezależnie od tego, jakie procesy zachodzą wewnątrz układu Zasady zachowania :-pędu, momentu pędu, e. mechanicznej,
2.1 Lagranżjan, L, inaczej funkcja Lagrange'a to gęstość funkcjonału działania S charakteryzującego własności mechaniczne układu fizycznego. Ruch układu w mechanice klasycznej opisywany jest za pomocą trajektorii x(t) podającej zależność położenia x od czasu t. Zgodnie z zasadą najmniejszego działania ruch układu mechanicznego przebiega w taki sposób, aby pewien funkcjonał S przyjmował najmniejszą możliwą wartość. Funkcjonał ten, nazywany działaniem, i oznaczany zwykle przez S, ma postać całki, zaś całkowanie przebiega po czasie:
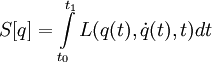
We wzorze tym
to lagranżjan.
Lagranżjan zdefiniowany jest wzorem:
gdzie T - energia kinetyczna, zas V - potencjał uogólniony
3.1 Symetrie czasoprzestrzenne:
Za uniwersalną własność przestrzeni uznaje się jej jednorodność (symetrię względem przesunięć), izotropię (symetrię względem obrotów) oraz zasadę względności (symetrię względem przekształceń Lorentza).
Przykłady symetrii:
Grupa przesunięć - inaczej translacji
Grupa obrotów SO(3) - symetria trójwymiarowej przestrzeni euklidesowej
Grupa Galileusza SO(3)xO(1) - symetria fizyki newtonowskiej (przestrzeni z czasem)
Grupa Lorentza SO(3,1) - symetria Teorii względności (czasoprzestrzeni, przestrzeni Minkowskiego)
Grupa Poincarego - grupa Lorentza wraz z przesunięciami, symetria teorii pól kwantowych
Odbicie przestrzenne P - inaczej odbicie lustrzane (jest to symetria przybliżona)
Odbicie czasowe T - odwrócenie biegu czasu (jest to symetria przybliżona)
3.2 Twierdzenie Noether dotyczy związku zasad zachowania z symetrią ciągłą.Twierdzenie to mówi, że każda ciągła symetria praw fizyki (która nie zmienia zasady wariacyjnej najmniejszego działania oraz równań ruchu opisujących układ), opisywana przez grupę Liego generuje tyle praw zachowania, ile jest niezależnych parametrów opisujących daną grupę Liego (lub generatorów grupy Liego).
3.3 Własności symetrii
3.4 Spontaniczne złamanie symetrii jest zjawiskiem fizycznym zachodzącym wówczas gdy stan podstawowy układu fizycznego ma niższą symetrię niż symetria układu fizycznego Złamane symetrie fizyczne stają się dopiero widoczne w wysokich energiach. Stany symetryczne względem złamanej symetrii mogą wtedy przekształcać się między sobą i stają się wtedy nieodróżnialne. Np. Ferromagnetyzm, teorie pól kwantowych, nadprzewodnictwo.
4.1 Układ inercjalny - układ odniesienia, względem którego każde ciało niepodlegające zewnętrznemu oddziaływaniu z czymkolwiek porusza się bez przyśpieszenia (tzn. ruchem jednostajnym prostoliniowym); zwany również układem "inercyjnym". Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki są w nich identyczne. Identyczne są również wszystkie prawa fizyki w układach inercjalnych. Uogólnienie tej zasady na układy nieinercjalne jest podstawową treścią ogólnej teorii względności.
Układ inercjalny - układ który spoczywa lub porusza się ruchem jednostajnym (bez przyspieszenia) - spełniona jest I zasada dynamiki Newtona.
4.2 Zasada względności głosi, że prawa fizyki w dwóch układach odniesienia poruszających się względem siebie ze stałą prędkością są takie same. Odkrył ją Galileusz.
4.3 Zasada korespondencji Jeśli jakaś wielkość A w mechanice klasycznej jest zależna od pędów i położeń, to w mechanice kwantowej operator jej można znaleźć wstawiając do klasycznego wzoru w miejsce pędów operatory pędów, a w miejsce położeń - operatory położeń.
4.4 Transformacja Lorentza - przekształcenie liniowe przestrzeni Minkowskiego zachowujące odległości. Odpowiada ono obrotowi w przestrzeni euklidesowej; cechą charakterystyczną jest niezmienniczość przekształcenia ze względu na prędkość światła.
W fizyce, transformacje Lorentza opisują zależności między współrzędnymi i czasem tego samego zdarzenia w dwóch inercjalnych układach odniesienia wg szczególnej teorii względności. Wg klasycznej mechaniki, zależność między czasem i współrzędnymi opisują transformacje Galileusza.
4.5 Prędkość nadświetlna Zgodnie ze szczególną teorią względności nic posiadającego energię nie może się poruszać szybciej niż światło w próżni. Prędkość nadświetlną (czyli większą od prędkości światła w próżni) mogą osiągać obiekty nie przenoszące informacji ani energii (np. cień, prędkość fazowa fali) i nie zaprzecza to szczególnej teorii względności. Na przykład prędkość fazowa światła w szkle jest większa od prędkości światła w próżni.
4.6 - może szybciej od C - światło w szkle szybciej niż w próżni
5.1 Względność równoczesności
Z tego że w jednym układzie zjawiska są równocześnie nie wynika że są równoczesne w innym układzie.
t1=t2 ∆t=0
t'=γ(t - [v/c2 ]*x)
∆t'= γ(∆t - [v/c2 ]* ∆ x)
∆t `=-γ[v/c2 ]*∆x
∆t=0 →∆t'≠0
5.2 następstwo zdarzeń
5.3 Dylatacja czasu i skr. Lorenza
Dylatacja czasu
Równoczesność zdarzeń jest względna - czas własny późni się w stosunku do innych poruszających się układów.
Skrócenie Lorenza
l0 = lγ l = l0√[1-(v/c)2] l0< l
-względem ukł. Inercjalnego
5.4 Paradoks bliźniąt
Wiek blizniaka najłatwiej policzyc wzgledem układu zwiazanego z bratem podróżnikiem, jego ukł.inercjalny sie nie zmienia. Zegar brata w kosmosie późni sie w stosunku do brata na ziemi.Brat podróżnik jest młodszy.
T'=T*√[1-(v/c)2]
5.5 Paradoks Korzeniowskiego
Zgodnie ze szczególną teoria względności wewnątrz obiektów poruszających się z b.duzymi prędkościami czas płynie wolniej dla obserwatorów zew. Należy sie spodziewac ze zegarek na ręku R.Korzeniowskiego będzie chodził wolnie. Powolniejsze będzie też bicie jego serca.
5.6 dylemat zwrotniczego
chyba chodzi o to, że w bardzo szybkim pociągu zegar tyka wolniej i czas jaki pokazuje jest inny niż na stacji. Zwrotniczy który ma nastawić zwrotnicę o danej godzinie ustawi ją tak że pociąg się wyjebie.
5.7 efekt unoszenia światła w poruszającym się ośrodku
chyba chodzi o to że światło wystrzelone z domu i z pociągu dotrze do celu w tym samym czasie. Nie ma znaczenia prędkość ośrodka emitującego światło.
5.8 Interwał czasoprzestrzenny - odległość czasoprzestrzenna. W przestrzeni Minkowskiego (bez uwzględnienia grawitacji) opisana jest wzorem:
gdzie
- interwał czasoprzestrzenny między dwoma zdarzeniami mierzony w inercjalnym układzie odniesienia U
i
to współrzędne zdarzeń w przestrzeni czterowymiarowej,
c - prędkość światła
Interwał między dwoma zdarzeniami jest niezmienniczy względem transformacji Lorentza.
6.1 Zasada zachowania e. i pędu w STW
E.całkowita cząstki E = γ * m * c2
p. cząstki p = γ * m * v
e.kinetyczna Ek = m*( γ- 1)*c2
e.wewnętrzna Ew = m* c2
E= Ek +Ew
6.2 Związek miedzy e. i pedem w STW
p(w)= γ * m * v(w) Ew = m* γ* c2
[p(w)/E] = [v(w)/c2] p(w)= [E*v(w)]/c2
m= [ √(E/c)2 - p2 ] /c
6.3 Niezmienniki, czterowektory,def masy.
Niezmienniki-(masa, dległość) - wielkosci które zachowuję sie przy przejściu z jednego układu do drugiego.
Czterowektor -wekt. scharakteryzowany przez 3 współrzedne (x,y,z) i wspołrzedną czasową np. czterowektor pędu:
Deficyt masy (niedobór masy, defekt masy) - różnica Δm między sumą mas nukleonów wchodzących w skład jądra atomowego, a masą jądra. Iloczyn niedoboru masy i kwadratu prędkości światła w próżni jest równy energii wiązania jądra, ΔE.
ΔE = Δmc2
gdzie:
Δm = Nmn + Zmp − mE(Z,N)
gdzie:
mp=1,00727 - masa protonu
mn=1,00866 - masa neutronu
mE - masa jądra atomowego
c = 3·108 m/s - prędkość światła w próżni
Masa nie jest addytywna, tzn. masa ciała nie jest równa sumie mas jego części składowych!
6.4 Energia, pęd i masa fotonu
p(w)= h / λ E= h * [c/ λ]
m= [1/c] * √[ (E/c)2 - p2 ] = 0
6.5 Masa w STW
masa gazu fotonowego mgf = N * [ (hυ)/c2 ]
m. jądra at. o j nukleonach
mj = 2 * j * m - (Ewj/c2)
Ewj=jmc2 - e. wiązania w jądrze
6.6 Równanie dynamiki w STW
F(wektor) = dp(w.)/dt p(w.)= γ * m*v(w)
F(w)=[d(m γv(w)]/dt
6.7 Przyspieszenie cząstki pod wpływem siły F
6.8 Akcja i reakcja w STW
6.9 pozyskiwanie energii jądrowej
Energia jądrowa to energia uzyskiwana na drodze kontrolowanych przemian jądrowych. Uzyskiwana jest głównie w wyniku rozszczepienia ciężkich jąder atomowych w niewielkim stopniu w wyniku rozpadów promieniotwórczych, trwają prace nad kontrolowanym przeprowadzaniem reakcji fuzji lekkich jąder atomowych.Reakcje rozszczepienia ciężkich jąder atomowych, głównie uranu-235, przeprowadza się w reaktorach atomowych, gdzie energia jądrowa zamienia się na energię wewnętrzną (cieplną).
6.10 ciśnieniowy reaktor wodny
Reaktor wodny ciśnieniowy, w skrócie PWR (ang. Pressurized Water Reactor) -- reaktor jądrowy, w którym moderatorem jest zwykła (lekka) woda pod ciśnieniem ok. 15 MPa. Woda spełnia jednocześnie funkcję czynnika roboczego - chłodziwa rdzenia reaktora. Reaktor PWR (RJ) produkuje gorącą wodę pod dużym ciśnieniem, która następnie trafia do wytwornicy pary (WP). Tam oddaje ciepło wodzie pod niższym ciśnieniem, która zmienia się w parę mokrą (zazwyczaj 275°C i 6 MPa). Dalej para ta rozpręża się na turbinie parowej (TP).
W odróżnieniu od reaktorów BWR, w reaktorach PWR stosowane są dwa obiegi czynnika roboczego. Pozwala to na zmniejszenie ryzyka wycieku radioaktywnych substancji.
Moc reaktora PWR regulowana jest przez zmianę stężenia boru (pod postacią kwasu borowego) w wodzie w obiegu pierwotnym. Grafitowe pręty regulacyjne stosowane są jedynie podczas rozruchu i wyłączania reaktora.
Reaktory PWR są bardzo bezpiecznymi konstrukcjami. Do tej pory miał miejsce tylko jeden poważny wypadek z ich udziałem. Reaktor PWR firmy Babcock & Wilcox uległ awarii 28 marca 1979 roku podczas wypadku w elektrowni Three Mile Island. Zastosowana obudowa bezpieczeństwa zapobiegła wyciekowi radioaktywnemu. Nikt nie zginął.
7.0 Fermilab CERN W 1976 ruszył akcelerator SPS (Super Proton Synchrotron) pozwalający przyspieszać protony do energii 300 GeV; dwa lata później po udoskonaleniu rozpędzał on już protony do energii 500 GeV
Akceleratory można klasyfikować ze względu na różne cechy:
rodzaj przyspieszanych cząstek, np. akceleratory protonów, elektronów, jonów ciężkich
kształt toru przyspieszanych cząstek: liniowe, kołowe (cykliczne)
metodę przyspieszania, np. napięcie stałe, wysokiej częstotliwości, indukowane, wielostopniowe
maksymalną energię przyspieszenia (keV, MeV, GeV)
gradient pola przyspieszającego (stałe, zmienne)
Cząstki przyspieszane są polem elektrycznym, pole magnetyczne stosuje się do nadania przyspieszanym cząstkom odpowiedniego toru lub skupienia ich.
Pole elektryczne jest tworzone przez specjalne układy generatorów bardzo wysokiego napięcia i przekazywane na układy elektrod. Pole magnetyczne jest tworzone przy pomocy bloków elektromagnesów, które są rozmieszczone co jakiś czas na całej linii/obwodzie akceleratora.
Akceleratory nie są urządzeniami uniwersalnymi, np. akcelerator przyspieszający cząstki lekkie, nie będzie mógł zostać użyty do przyspieszania ciężkich jonów. Wynika to z różnicy mas cząstek i progu energii, przy której znaczną rolę zaczynają odgrywać efekty relatywistyczne.
7.1 Główny podział akceleratorów uwzględnia kształt toru i metodę przyspieszania:
liniowe - cząstki przyspieszane są na odcinku prostym:
o stałym napięciu przyspieszającym (kaskadowy, van der Graaffa, tandem Cockcrofta-Waltona)
o napięciu przyspieszającym wysokiej częstotliwości (liniowy z falą bieżącą, liniowy z falą stojącą).
Cykliczne (kołowe)
synchroniczne (cyklotron, synchrocyklotron, synchrotron protonowy, synchrotron elektronowy, mikrotron)
asynchroniczne (betatron, akcelerator plazmowy, akcelerator wiązek przeciwbieżnych)
są obawy że gdy przyspieszymy cząstkę do C to powstanie :
Czarna dziura - obiekt astronomiczny, który tak silnie oddziałuje grawitacyjnie na swoje otoczenie, że nawet światło nie może uciec z jego powierzchni. Żaden rodzaj energii ani materii nie może opuścić czarnej dziury
Uwolnienie energii próżni Wiele obserwacji wskazuje, że nasz Wszechświat posiada niezerową energię próżni. Jeżeli istnieje stan próżni o niższej energii, to Wszechświat jest w stanie próżni fałszywej i może dojść do tunelowania do niższego stanu. Będzie się to wiązać ze zmianą niektórych "stałych" fizycznych, np. mas wielu cząstek. Nastąpi też koniec takiego Wszechświata, jaki znamy, ponieważ np. atomy mogą stać się nietrwałe.
8.1 odcięcie Greisena Zecepina Kuźmina
8.2 Rozbłyski gamma (GRB, z ang. Gamma-Ray Bursts) - pojawiające się w całym obszarze sfery niebieskiej mniej więcej raz na dobę i trwające od kilku sekund aż do godziny, nagłe wzrosty promieniowania gamma w niewielkim obszarze nieba. Zostały po raz pierwszy zaobserwowane pod koniec lat 60. XX w..
9.1 Tw. Gaussa i Stokes'a
Tw.G - strumień pola el. przechodzącego przez zamkniętą pow. jest równy całkowitemu ładunkowi el. zamkniętemu w tej pow. ε0ΦE = q ,
[ε0 - wspołczynnik przenikalności el. próżni
ΦE - strumień pola. el.
q- ładunek el.] ponieważ: ΦE = ∫EdS, to prawo G. przyjmuje postać: ε0∫EdS=q
Tw. S.- wzór całkowity teorii pola, wiążący teorie pola wektorowego a wzdłóż pewniej krzywej zamkniętej L (konturu ograniczajacego pow. S) z wart. rotacji tego pola.
∫a*dr =∫∫n * rotad S
L S
[dr-element. wektor należący do konturu L,n-wekt. normalny do pow.S
9.2. równania maxwella
postać rózniczkowa:
▼ (kreska nad)E(kn)= ρ/ε0
▼ (kn)B(kn)=0
▼ (kn)xE(kn)= - [ ∂B/∂t ]
c2▼(kn)xB(kn)= (j/ ε0) + (∂B/∂t)
całkowa:
∫EdS= q/ε0
∫BdS=0
∫Edl= - [ (dφB) / dt ]
∫Bdl = μ0 (ε0 [ dφE /dt ] + i )
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
Wielkości fizyczne |
Wzór klasyczny |
Wzór relatywistyczny |
Pęd |
|
|
Siła |
|
|
Energia całkowita |
|
|
Energia kinetyczna |
|
|
![]()
Wyszukiwarka
Podobne podstrony:
propedeutyka pediatrii - suplement do opracowania (semestr letni), Pediatria
rdim Opracowanie, Semestr V, RDiM
chłody opracowanie, semestr 6-7
propedeutyka pediatrii - opracowanie (semestr letni), Pediatria
ćw z 24 kwietnia 2001, LEŚNICTWO SGGW, MATERIAŁY LEŚNICTWO SGGW, Urządzanie, Wykłady, Urządzanie- op
Egzamin z botaniki OPRACOWANIE, Semestr 2, Botanika
Opracowanie, Semestr3, Teoria Systemów
pytania+opracowanie, semestr 4, ekologia
anatomia opracowanie semestr I, Studium kosmetyczne, Anatomia
AUTOMATY opracowanie, Semestr IV, Wspólne, Podstawy automatyki
1 kolowium - opracowanie, E i T, semestr VI
temp krytyczna, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Fizyka - Opracowane pojęcia 1, Budownictwo S1, Semestr I, Fizyka
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
opracowanie cw 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
Opracowanie Cw 7, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
więcej podobnych podstron